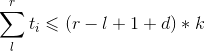【BZOJ】【P1135】【POI2009】【Lyz】【题解】【线段树+Hall定理】

传送门：http://www.lydsy.com/JudgeOnline/problem.php?id=1135

把鞋子和人抽象成二分图

Hall定理：

此定理使用于组合问题中， 二部图G中的两部分顶点组成的集合分别为X, Y, X={X1, X2, X3,X4, .........,Xm}, Y={y1, y2, y3, y4 , .........,yn},G中有一组无公共点的边，一端恰好为组成X的点的充分必要条件是：

X中的任意k个点至少与Y中的k个点相邻。（1≤k≤m)

那么有解的条件就是任意一个人的集合的人数<=所连接的鞋子数量,对于序列来说连续子序列就够了(我不知道为什么……)

用  表示鞋号为i的人的个数

那么

令

则

维护t'i的最长连续子序列

Code:

#include<cstdio>
#include<iostream>
#include<algorithm>
using namespace std;
const int maxn=2e5+5;
typedef long long LL;
struct seg{
	struct node{
		LL ls,rs,ss,sum;
		node(){ls=rs=ss=sum=0;}
	}t[maxn<<2];
	#define lson i<<1,l,mid
	#define rson i<<1|1,mid+1,r
	#define L i<<1
	#define R i<<1|1
	void Add(int i,int l,int r,int ps,LL d){
		if(l==r){t[i].ls+=d;t[i].rs+=d;t[i].ss+=d;t[i].sum+=d;return;}
		int mid=(l+r)>>1;
		if(ps<=mid)Add(lson,ps,d);else Add(rson,ps,d);
		t[i].ls=max(t[L].ls,t[L].sum+t[R].ls);
		t[i].rs=max(t[R].rs,t[R].sum+t[L].rs);
		t[i].ss=max(t[L].ss,t[R].ss);
		t[i].ss=max(t[i].ss,t[L].rs+t[R].ls);
		t[i].sum=t[L].sum+t[R].sum;
	}	
}T;
int n,m,k,d;
int main(){
	scanf("%d%d%d%d",&n,&m,&k,&d);
	for(int i=1;i<=n;i++)T.Add(1,1,n,i,-k);
	while(m--){
		int x,r;scanf("%d%d",&r,&x);
		T.Add(1,1,n,r,x);
		puts(T.t[1].ss<=(LL)d*k?"TAK":"NIE");
	}
	return 0;
}