SVD and PCA
MIT 线性代数课程中讲过的矩阵分解有很多种,但是据我所知最重要的应该是SVD分解了,假如现在想把矩阵A行空间的正交基通过A左乘的方法变换到A列空间的正交基,有:
将上式左右两边都乘以V的转置,就可以得到矩阵奇异值分解的公式,SVD的分解式子如下(矩阵A从这里开始用X表示):
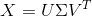
将上式左右两边都乘以V的转置,就可以得到矩阵奇异值分解的公式,SVD的分解式子如下(矩阵A从这里开始用X表示):
假如原来X是m*n的矩阵,那么U一般是m*r,sigma一般是r*r,V一般是n*r,
V的每列都是行空间的标准正交基,U的每列都是列空间的标准正交基。
这个r一般选取的是Rank(X),但有时也可以近似分解,选择r<rank(X)。
这里需要说明的一点是,其实U可以写成m*m,sigma写成m*n,V写成n*n,在这样的情况下,
sigma中有很多0的元素,所以U中的后面几列和V中的后面几列是对于乘法是没有作用的,
这里省去,但是如果非要写成m*m,m*n,n*n的形式,则在U的后面几列后面补上X的零空间
的正交基和V的后面几列补上X的左零空间的正交基即可。
一般来说,sigma是一个对角矩阵,且对角线元素是方阵![]() 和方阵
和方阵![]() 特征值的正平方根,
特征值的正平方根,
且按照降序排放。可以发现,V的每列都是![]() 的特征向量,U的每列都是
的特征向量,U的每列都是![]() 的特征向量,
的特征向量,
第i列的特征向量对应的特征值是![]() ,他们分别都是按照特征值下降的顺序排放。
,他们分别都是按照特征值下降的顺序排放。
SVD能解决哪些问题呢?第一就是解决PCA,可以发现
这个式子左边的矩阵,其实就是X这个数据集(已经预处理,均值为0)协方差矩阵(设为M)的前K个特征值所对应的特征向量转置排列后而成。由于数据已经预处理,根据协方差矩阵的计算公式,易得![]() =(n-1)*M(n是样本个数),因此
=(n-1)*M(n是样本个数),因此![]() 与M所对应特征向量是相同的,如果奇异值分解也取近似(取r=k<Rank(X)),只需要用SVD分解后的
与M所对应特征向量是相同的,如果奇异值分解也取近似(取r=k<Rank(X)),只需要用SVD分解后的![]() 乘以X就能得到PCA降维后的X'。
乘以X就能得到PCA降维后的X'。

