ChiMerge 算法

基本思想

ChiMerge 是监督的、自底向上的(即基于合并的)数据离散化方法。它依赖于卡方检验：具有最小卡方值的相邻区间合并在一起，直到满足确定的停止准则。
基本思想：对于精确的离散化，相对类频率在一个区间内应当完全一致。因此，如果两个相邻的区间具有非常类似的类分布，则这两个区间可以合并；否则，它们应当保持分开。而低卡方值表明它们具有相似的类分布。
参考
参考：
1. ChiMerge:Discretization of numeric attributs
2. Chi算法
要点

1、 最简单的离散算法是： 等宽区间。 从最小值到最大值之间,，均分为 N 等份， 这样， 如果 A,B 为最小最大值， 则每个区间的长度为 W=(B−A)/N , 则区间边界值为 A+W,A+2W,….A+(N−1)W .
2、 还有一种简单算法，等频区间。区间的边界值要经过选择，使得每个区间包含大致相等的实例数量。比如说 N=10 ，每个区间应该包含大约10%的实例。
3、 以上两种算法有弊端：比如，等宽区间划分，划分为5区间，最高工资为50000，则所有工资低于10000的人都被划分到同一区间。等频区间可能正好相反，所有工资高于50000的人都会被划分到50000这一区间中。这两种算法都忽略了实例所属的类型，落在正确区间里的偶然性很大。
4、 C4、CART、PVM 算法在离散属性时会考虑类信息，但是是在算法实施的过程中间，而不是在预处理阶段。例如， C4 算法（ID3决策树系列的一种），将数值属性离散为两个区间，而取这两个区间时，该属性的信息增益是最大的。
5、 评价一个离散算法是否有效很难，因为不知道什么是最高效的分类。
6、 离散化的主要目的是：消除数值属性以及为数值属性定义准确的类别。
7、 高质量的离散化应该是：区间内一致，区间之间区分明显。
8、 ChiMerge 算法用卡方统计量来决定相邻区间是否一致或者是否区别明显。如果经过验证，类别属性独立于其中一个区间，则这个区间就要被合并。
9、 ChiMerge算法包括2部分：1、初始化，2、自底向上合并，当满足停止条件的时候，区间合并停止。

步骤
第一步：初始化
根据要离散的属性对实例进行排序：每个实例属于一个区间
第二步：合并区间，又包括两步骤
(1) 计算每一对相邻区间的卡方值
(2) 将卡方值最小的一对区间合并
预先设定一个卡方的阈值，在阈值之下的区间都合并，阈值之上的区间保持分区间。
卡方的计算公式：

χ2=∑mi=1∑kj=1(Aij−Eij)2Eij

参数说明：
m=2 ，每次比较两个相邻区间，2个区间比较
k= 类别的数量
Aij= 第 i 区间第 j 类的实例数量
Ri= 第 i 区间的实例数量

Ri=∑kj=1Aij

Cj= 第 j 类的实例数量

Cj=∑mi=1Aij

N= 总的实例数量

N=∑kj=1Cj

Eij=Aij 的期望

Eij=Ni∗CjN

10、卡方阈值的确定：先选择显著性水平，再由公式得到对应的卡方值。得到卡方值需要指定自由度，自由度比类别数量小1。例如，有3类，自由度为2，则90%置信度（10%显著性水平)下，卡方的值为4.6。阈值的意义在于，类别和属性独立时，有90%的可能性，计算得到的卡方值会小于4.6，这样，大于阈值的卡方值就说明属性和类不是相互独立的，不能合并。如果阈值选的大，区间合并就会进行很多次，离散后的区间数量少、区间大。用户可以不考虑卡方阈值，此时，用户可以考虑这两个参数：最小区间数，最大区间数。用户指定区间数量的上限和下限，最多几个区间，最少几个区间。
11、 ChiMerge算法推荐使用0.90、0.95、0.99置信度，最大区间数取10到15之间.
12.以iris数据距离说明



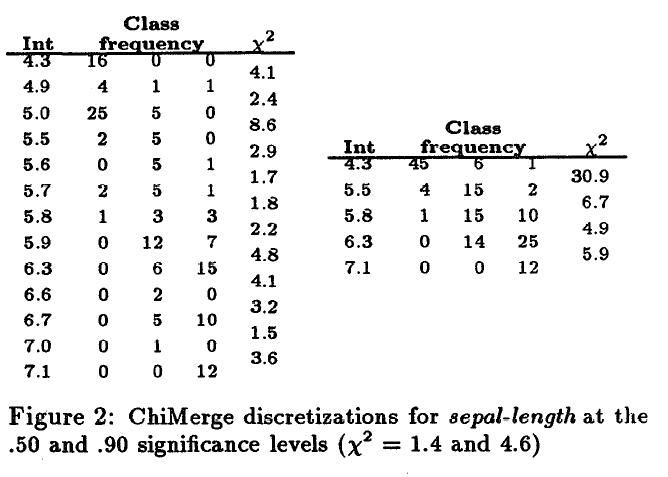
图二：左边第一列是 sepal−length 属性值，中间三列是三个类在该属性值下对应的实例数量，最后一列是卡方值。区间为相邻两行第一列属性所构成的区间，如 [4.3,4.9) ，前闭后开。卡方值越大说明该区间和下一个区间的差别越大，如 [5.0,5.5) 和下一个区间 [5.5,5.6) ,说明 [5.5,5.6) 不会和 [5.0,5.5) 合并到一个区间，左边采用的是卡方值是1.4（0.5显著水平）下的阈值得到的离散结果，右边是采用卡方值是4.6（0.9的显著水平）的阈值得到的离散结果。

举例：
取鸢尾花数据集作为待离散化的数据集合，使用ChiMerge算法，对四个数值属性分别进行离散化，令停机准则为max_interval=6。
下面是我用Python写的程序，大致分两步：
第一步，整理数据
读入鸢尾花数据集，构造可以在其上使用ChiMerge的数据结构，即, 形如 [(‘4.3’, [1, 0, 0]), (‘4.4’, [3, 0, 0]),…]的列表，每一个元素是一个元组，元组的第一项是字符串，表示区间左端点，元组的第二项是一个列表，表示在此区间各个类别的实例数目；
第二步，离散化
使用ChiMerge方法对具有最小卡方值的相邻区间进行合并，直到满足最大区间数(max_interval)为6
程序最终返回区间的分裂点
Python实现：

# coding=utf-8
from time import ctime
''' 读取数据'''
def read(file):
    Instances = []
    fp = open(file,'r')
    for line in fp:
        line = line.strip('\n')
        if line!='':
            Instances.append(line.split(','))
    fp.close()
    return Instances
''' 将第i个特征和类标签组合起来 如:[[0.2,'Iris-setosa'],[0.2,'Iris-setosa'],...]'''
def split(Instances,i):
    log = [] 
    for line in Instances:
        log.append([line[i],line[4]])
    return log 
''' 统计每个属性值所具有的实例数量 [['4.3', 'Iris-setosa', 1], ['4.4', 'Iris-setosa', 3],...]'''  
def count(log):
    log_cnt = []
    # 以第0列进行排序的 升序排序
    log.sort(key = lambda log:log[0])
    i = 0
    while(i<len(log)):
        cnt = log.count(log[i])
        record = log[i][:]
        record.append(cnt)
        log_cnt.append(record)
        i += cnt 
    return log_cnt

''' log_cnt 是形如： ['4.4', 'Iris-setosa', 3] 的 统计对于某个属性值，对于三个类所含有的数量量 返回结果形如：{4.4:[0,1,3],...} 属性值为4.4的对于三个类的实例数量分别是：0、1、3 '''
def build(log_cnt):
    log_dict = {}
    for record in log_cnt:
        if record[0] not in log_dict.keys():
            log_dict[record[0]] = [0,0,0]
        if record[1] == 'Iris-setosa':
            log_dict[record[0]][0] = record[2]
        elif record[1] == 'Iris-versicolor':
            log_dict[record[0]][1] = record[2]
        elif record[1] == 'Iris-virginica':
            log_dict[record[0]][2] = record[2]
        else:
            raise TypeError('Data Exception')
    log_truple = sorted(log_dict.items())
    return log_truple

def collect(Instances,i):
    log = split(Instances,i)
    log_cnt = count(log)
    log_tuple = build(log_cnt)
    return log_tuple

def combine(a,b):
    ''''' a=('4.4', [3, 1, 0]), b=('4.5', [1, 0, 2]) combine(a,b)=('4.4', [4, 1, 2]) '''  
    c = a[:]
    for i in range(len(a[1])):
        c[1][i] += b[1][i]
    return c 

def chi2(A):
    '''计算两个区间的卡方值'''
    m = len(A)
    k = len(A[0])
    R = []
    '''第i个区间的实例数'''
    for i in range(m):
        sum = 0
        for j in range(k):
            sum += A[i][j]
        R.append(sum)
    C = []
    '''第j个类的实例数'''
    for j in range(k):
        sum = 0
        for i in range(m):
            sum+= A[i][j]
        C.append(sum)
    N = 0
    '''总的实例数'''
    for ele in C:
        N +=ele
    res = 0.0
    for i in range(m):
        for j in range(k):
            Eij = 1.0*R[i] *C[j]/N 
            if Eij!=0:
                res = 1.0*res + 1.0*(A[i][j] - Eij)**2/Eij
    return res 

'''ChiMerge 算法'''
'''下面的程序可以看出，合并一个区间之后相邻区间的卡方值进行了重新计算，而原作者论文中是计算一次后根据大小直接进行合并的 下面在合并时候只是根据相邻最小的卡方值进行合并的，这个在实际操作中还是比较好的 '''
def ChiMerge(log_tuple,max_interval):
    num_interval = len(log_tuple)
    while num_interval>max_interval:
        num_pair = num_interval -1
        chi_values = []
        ''' 计算相邻区间的卡方值'''
        for i in range(num_pair):
            arr = [log_tuple[i][1],log_tuple[i+1][1]]
            chi_values.append(chi2(arr))
        min_chi = min(chi_values)
        for i in range(num_pair - 1,-1,-1):
            if chi_values[i] == min_chi:
                log_tuple[i] = combine(log_tuple[i],log_tuple[i+1])
                log_tuple[i+1] = 'Merged'
        while 'Merged' in log_tuple:
            log_tuple.remove('Merged')
        num_interval = len(log_tuple)
    split_points = [record[0] for record in log_tuple]
    return split_points

def discrete(path):
    Instances = read(path)
    max_interval = 6
    num_log = 4
    for i in range(num_log):
        log_tuple = collect(Instances,i)
        split_points = ChiMerge(log_tuple,max_interval)
        print split_points

if __name__=='__main__':  
    print('Start: ' + ctime())  
    discrete('iris.data')  
    print('End: ' + ctime())  

结果

Start: Sat Jan 02 21:33:26 2016
['4.3', '4.9', '5.0', '5.5', '5.8', '7.1']
['2.0', '2.3', '2.5', '2.9', '3.0', '3.4']
['1.0', '3.0', '4.5', '4.8', '5.0', '5.2']
['0.1', '1.0', '1.4', '1.7', '1.8', '1.9']
End: Sat Jan 02 21:33:26 2016

资料来源：http://blog.csdn.net/zhaoyl03/article/details/8689440

利用R自带函数运行

library(discretization)
#--Discretization using the ChiMerge method data(iris) disc=chiM(iris,alpha=0.05) #--cut-points disc$cutp #--discretized data matrix disc$Disc.data

结果

> disc$cutp
[[1]]
[1] 5.45 5.75 7.05

[[2]]
[1] 2.95 3.35

[[3]]
[1] 2.45 4.75 5.15

[[4]]
[1] 0.80 1.75

还是有点差别的
0.9的显著水平时候

disc=chiM(iris,alpha=0.1)
#--cut-points
disc$cutp

结果

disc$cutp
[[1]]
[1] 4.85 4.95 5.45 5.75 6.25 7.05

[[2]]
[1] 2.45 2.85 2.95 3.35

[[3]]
[1] 2.45 4.75 5.15

[[4]]
[1] 0.80 1.35 1.75

和原作者论文中计算结果很接近了。但是在作者论文中先对数据进行了处理，Sepal.Length这个属性，直接把小于4.9 的归为一类 大于7.1的归为一类，和R自带函数运行的结果却很相似，可能也对两端数据进行了预处理。
但是为什么不是合并两个区间后重新计算相邻区间的卡方值，再进行合并？
R语言中计算分裂点的函数：

 value <- function (i, data, alpha) 
{
    p1 <- length(data[1, ])
    p <- p1 - 1
    y <- as.integer(data[, p1])
    class <- dim(table(data[, p1]))
    discredata <- data
    threshold <- qchisq(1 - alpha, class - 1)
    cuts <- numeric()
    z <- sort(unique(data[, i]))
    if (length(z) <= 1) 
        return(list(cuts = "", disc = discredata))
    dff <- diff(z)/2
    lenz <- length(z)
    cutpoint <- z[1:(lenz - 1)] + dff
    midpoint <- c(z[1], cutpoint, z[lenz])
    a <- cut(data[, i], breaks = midpoint, include.lowest = TRUE)
    b <- table(a, data[, p1])
    b <- as.array(b)
    repeat {
        m <- dim(b)[1]
        if (length(dim(b)) < 2 || m < 2) 
            break
        test <- numeric()
        for (k in 1:(m - 1)) {
            d <- b[c(k, k + 1), ]
            test[k] = chiSq(d)
        }
        k <- which.min(test)
        if (test[k] > threshold) 
            break
        b[k + 1, ] <- b[k, ] + b[k + 1, ]
        cutpoint <- cutpoint[-k]
        midpoint <- midpoint[-(k + 1)]
        b <- b[-k, ]
    }
    cuts <- cutpoint
    discredata[, i] <- cut(data[, i], breaks = midpoint, include.lowest = TRUE, 
        label = FALSE)
    return(list(cuts = cuts, disc = discredata))
}

说明：在上面是在 1−α 显著水平下 class−1 自由度下的卡方值
在进行计算每个区间的卡方值的时候有这个预处理

    dff <- diff(z)/2
    lenz <- length(z)
    cutpoint <- z[1:(lenz - 1)] + dff
    midpoint <- c(z[1], cutpoint, z[lenz])
    a <- cut(data[, i], breaks = midpoint, include.lowest = TRUE)
    b <- table(a, data[, p1])
    b <- as.array(b)

z是相邻两个数据的差值，再以diff/2为步长，说明白点就在不是严格按照当前点为区间分裂的边界，而是以两个点的中间点为分裂边界。
后面的程序也是每次合并两个，直到最后只有一个区间或者最小计算卡方值大于指定的卡方阈值了。
按照上面对 chiMerge 稍作改动

'''ChiMerge 算法'''
def ChiMerge2(log_tuple,max_chi):
    num_interval = len(log_tuple)
    while num_interval>2:
        num_pair = num_interval -1
        chi_values = []
        ''' 计算相邻区间的卡方值'''
        for i in range(num_pair):
            arr = [log_tuple[i][1],log_tuple[i+1][1]]
            chi_values.append(chi2(arr))
        min_chi = min(chi_values)
        if min_chi> max_chi:
            break
        for i in range(num_pair - 1,-1,-1):
            if chi_values[i] == min_chi:
                log_tuple[i] = combine(log_tuple[i],log_tuple[i+1])
                log_tuple[i+1] = 'Merged'
        while 'Merged' in log_tuple:
            log_tuple.remove('Merged')
        num_interval = len(log_tuple)
    split_points = [record[0] for record in log_tuple]
    return split_points

输出结果的切分点是：

['4.3', '4.9', '5.0', '5.5', '5.8', '6.3', '7.1']
['2.0', '2.5', '2.9', '3.0', '3.4']
['1.0', '3.0', '4.8', '5.2']
['0.1', '1.0', '1.4', '1.8']

这里是 maxchi=4.6 也就是说，显著水平0.9，自由度是3
而R的输出结果是：

disc$cutp
[1] 4.85 4.95 5.45 5.75 6.25 7.05
[2] 2.45 2.85 2.95 3.35
[3] 2.45 4.75 5.15
[4] 0.80 1.35 1.75

上面Python中输出的有左侧最小边界的，和R的输出差别主要是0.05，由于R考虑的是两个点的中间点进行合并的。