什么是二叉堆?
二叉堆是一种特殊的堆。具有如下的特性:
- 具有完全二叉树的特性。
- 堆中的任何一个父节点的值都大于等于它左右孩子节点的值(最大堆),或者都小于等于它左右孩子节点的值(最小堆)。
这个为最大堆:
这个为最小堆:
我们把二叉堆的根节点称之为堆顶。根据二叉堆的特性,堆顶要嘛是整个堆中的最大元素,要嘛是最小元素。
不过这里需要注意的是,在二叉堆这种结构中,对于删除一个节点,我们一般删的是根节点。
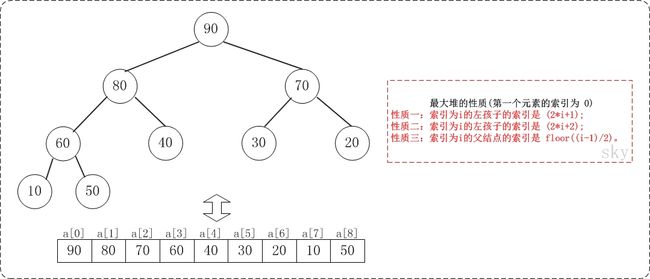
假设"第一个元素"在数组中的索引为 0 的话,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引是 (2*i+1);
- 索引为i的右孩子的索引是 (2*i+2);
- 索引为i的父结点的索引是 floor((i-1)/2);
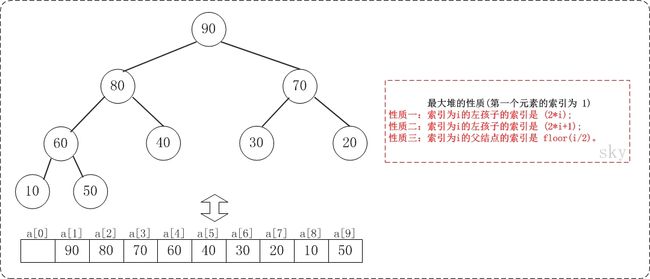
假设"第一个元素"在数组中的索引为 1 的话,则父节点和子节点的位置关系如下:
- 索引为i的左孩子的索引是 (2*i);
- 索引为i的右孩子的索引是 (2*i+1);
- 索引为i的父结点的索引是 floor(i/2);
二叉堆的图文解析
在前面,我们已经了解到:"最大堆"和"最小堆"是对称关系。这也意味着,了解其中之一即可。本节的图文解析是以"最大堆"来进行介绍的。
二叉堆的核心是"添加节点"和"删除节点",理解这两个算法,二叉堆也就基本掌握了。下面对它们进行介绍。
1. 添加
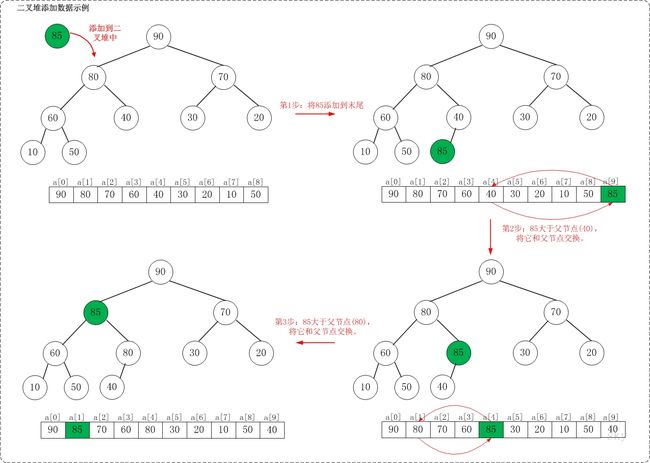
假设在最大堆[90,80,70,60,40,30,20,10,50]种添加85,需要执行的步骤如下:
如上图所示,当向最大堆中添加数据时:先将数据加入到最大堆的最后,然后尽可能把这个元素往上挪,直到挪不动为止!
将85添加到[90,80,70,60,40,30,20,10,50]中后,最大堆变成了[90,85,70,60,80,30,20,10,50,40]。
最大堆的插入代码(C语言)
/*
* 最大堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
static void maxheap_filterup(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-1)/2; // 父(parent)结点的位置
int tmp = m_heap[c]; // 当前节点(current)的大小
while(c > 0)
{
if(m_heap[p] >= tmp)
break;
else
{
m_heap[c] = m_heap[p];
c = p;
p = (p-1)/2;
}
}
m_heap[c] = tmp;
}
/*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
int maxheap_insert(int data)
{
// 如果"堆"已满,则返回
if(m_size == m_capacity)
return -1;
m_heap[m_size] = data; // 将"数组"插在表尾
maxheap_filterup(m_size); // 向上调整堆
m_size++; // 堆的实际容量+1
return 0;
}maxheap_insert(data)的作用:将数据data添加到最大堆中。
当堆已满的时候,添加失败;否则data添加到最大堆的末尾。然后通过上调算法重新调整数组,使之重新成为最大堆。
2. 删除
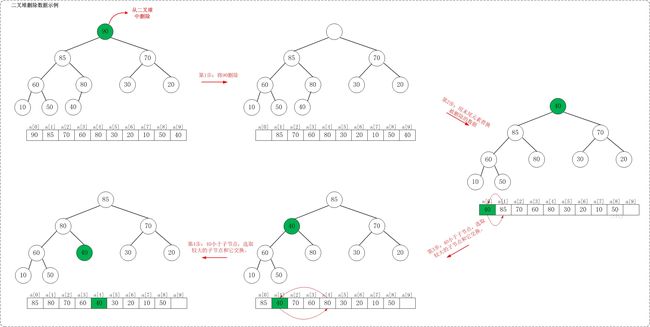
假设从最大堆[90,85,70,60,80,30,20,10,50,40]中删除90,需要执行的步骤如下:
从[90,85,70,60,80,30,20,10,50,40]删除90之后,最大堆变成了[85,80,70,60,40,30,20,10,50]。
如上图所示,当从最大堆中删除数据时:先删除该数据,然后用最大堆中最后一个的元素插入这个空位;接着,把这个“空位”尽量往上挪,直到剩余的数据变成一个最大堆。
注意:考虑从最大堆[90,85,70,60,80,30,20,10,50,40]中删除60,执行的步骤不能单纯的用它的子节点来替换;而必须考虑到"替换后的树仍然要是最大堆"!
最大堆的删除代码(C语言)
/*
* 返回data在二叉堆中的索引
*
* 返回值:
* 存在 -- 返回data在数组中的索引
* 不存在 -- -1
*/
int get_index(int data)
{
int i=0;
for(i=0; i= m_heap[l])
break; //调整结束
else
{
m_heap[c] = m_heap[l];
c = l;
l = 2*l + 1;
}
}
m_heap[c] = tmp;
}
/*
* 删除最大堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
int maxheap_remove(int data)
{
int index;
// 如果"堆"已空,则返回-1
if(m_size == 0)
return -1;
// 获取data在数组中的索引
index = get_index(data);
if (index==-1)
return -1;
m_heap[index] = m_heap[--m_size]; // 用最后元素填补
maxheap_filterdown(index, m_size-1); // 从index位置开始自上向下调整为最大堆
return 0;
} maxheap_remove(data)的作用:从最大堆中删除数据data。
当堆已经为空的时候,删除失败;否则查处data在最大堆数组中的位置。找到之后,先用最后的元素来替换被删除元素;然后通过下调算法重新调整数组,使之重新成为最大堆。
该"示例的完整代码"以及"最小堆的相关代码",请参考下面的二叉堆的实现。
二叉堆的C实现(完整源码)
二叉堆的实现同时包含了"最大堆"和"最小堆",它们是对称关系;理解一个,另一个就非常容易懂了。
二叉堆(最大堆)的实现文件(max_heap.c)
/**
* 二叉堆(最大堆)
*
* @author skywang
* @date 2014/03/07
*/
#include
#include
#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )
static int m_heap[30]; // 数据
static int m_capacity=30; // 总的容量
static int m_size=0; // 实际容量(初始化为0)
/*
* 返回data在二叉堆中的索引
*
* 返回值:
* 存在 -- 返回data在数组中的索引
* 不存在 -- -1
*/
int get_index(int data)
{
int i=0;
for(i=0; i= m_heap[l])
break; //调整结束
else
{
m_heap[c] = m_heap[l];
c = l;
l = 2*l + 1;
}
}
m_heap[c] = tmp;
}
/*
* 删除最大堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
int maxheap_remove(int data)
{
int index;
// 如果"堆"已空,则返回-1
if(m_size == 0)
return -1;
// 获取data在数组中的索引
index = get_index(data);
if (index==-1)
return -1;
m_heap[index] = m_heap[--m_size]; // 用最后元素填补
maxheap_filterdown(index, m_size-1); // 从index位置开始自上向下调整为最大堆
return 0;
}
/*
* 最大堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
static void maxheap_filterup(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-1)/2; // 父(parent)结点的位置
int tmp = m_heap[c]; // 当前节点(current)的大小
while(c > 0)
{
if(m_heap[p] >= tmp)
break;
else
{
m_heap[c] = m_heap[p];
c = p;
p = (p-1)/2;
}
}
m_heap[c] = tmp;
}
/*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
int maxheap_insert(int data)
{
// 如果"堆"已满,则返回
if(m_size == m_capacity)
return -1;
m_heap[m_size] = data; // 将"数组"插在表尾
maxheap_filterup(m_size); // 向上调整堆
m_size++; // 堆的实际容量+1
return 0;
}
/*
* 打印二叉堆
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
void maxheap_print()
{
int i;
for (i=0; i 二叉堆(最小堆)的实现文件(min_heap.c)
/**
* 二叉堆(最小堆)
*
* @author skywang
* @date 2014/03/07
*/
#include
#include
#define LENGTH(a) ( (sizeof(a)) / (sizeof(a[0])) )
static int m_heap[30];
static int m_capacity=30; // 总的容量
static int m_size=0; // 实际容量(初始化为0)
/*
* 返回data在二叉堆中的索引
*
* 返回值:
* 存在 -- 返回data在数组中的索引
* 不存在 -- -1
*/
int get_index(int data)
{
int i=0;
for(i=0; i m_heap[l+1])
l++; // 左右两孩子中选择较小者,即m_heap[l+1]
if(tmp <= m_heap[l])
break; //调整结束
else
{
m_heap[c] = m_heap[l];
c = l;
l = 2*l + 1;
}
}
m_heap[c] = tmp;
}
/*
* 删除最小堆中的data
*
* 返回值:
* 0,成功
* -1,失败
*/
int minheap_remove(int data)
{
int index;
// 如果"堆"已空,则返回-1
if(m_size == 0)
return -1;
// 获取data在数组中的索引
index = get_index(data);
if (index==-1)
return -1;
m_heap[index] = m_heap[--m_size]; // 用最后元素填补
minheap_filterdown(index, m_size-1); // 从index号位置开始自上向下调整为最小堆
return 0;
}
/*
* 最小堆的向上调整算法(从start开始向上直到0,调整堆)
*
* 注:数组实现的堆中,第N个节点的左孩子的索引值是(2N+1),右孩子的索引是(2N+2)。
*
* 参数说明:
* start -- 被上调节点的起始位置(一般为数组中最后一个元素的索引)
*/
static void filter_up(int start)
{
int c = start; // 当前节点(current)的位置
int p = (c-1)/2; // 父(parent)结点的位置
int tmp = m_heap[c]; // 当前节点(current)的大小
while(c > 0)
{
if(m_heap[p] <= tmp)
break;
else
{
m_heap[c] = m_heap[p];
c = p;
p = (p-1)/2;
}
}
m_heap[c] = tmp;
}
/*
* 将data插入到二叉堆中
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
int minheap_insert(int data)
{
// 如果"堆"已满,则返回
if(m_size == m_capacity)
return -1;
m_heap[m_size] = data; // 将"数组"插在表尾
filter_up(m_size); // 向上调整堆
m_size++; // 堆的实际容量+1
return 0;
}
/*
* 打印二叉堆
*
* 返回值:
* 0,表示成功
* -1,表示失败
*/
void minheap_print()
{
int i;
for (i=0; i 二叉堆的C测试程序
测试程序已经包含在相应的实现文件中了,这里就不再重复说明了。
最大堆(max_heap.c)的运行结果:
== 依次添加: 10 40 30 60 90 70 20 50 80
== 最 大 堆: 90 80 70 60 40 30 20 10 50
== 添加元素: 85
== 最 大 堆: 90 85 70 60 80 30 20 10 50 40
== 删除元素: 90
== 最 大 堆: 85 80 70 60 40 30 20 10 50最小堆(min_heap.c)的运行结果:
== 依次添加: 80 40 30 60 90 70 10 50 20
== 最 小 堆: 10 20 30 50 90 70 40 80 60
== 添加元素: 15
== 最 小 堆: 10 15 30 50 20 70 40 80 60 90
== 删除元素: 10
== 最 小 堆: 15 20 30 50 90 70 40 80 60