快速傅里叶变换FFT

前言

本文着重讲述FFT的简单原理，让朋友们阅读完本篇文章之后能够对快速傅里叶变换有一个大致概念。至于算法的具体数学论证，由于涉及到的数学知识比较多博主自己也没有搞懂，想要了解的朋友推荐这两篇文章传送门1，传送门2以及算法导论（第三版）第30章。

多项式

多项式有两种表达方式，一种是我们熟悉的系数表达式,对于n次多项式A，可以表示为

A(x)=∑i=0n−1aixi

也就是

A(x)=a0+a1x1+a2x2+⋅⋅⋅+an−1xn−1

另一种就是点值表达式，一个n次多项式要用n个点对组成集合， A(x) 用点值表达式可以写成

A(x)={(x0,y0),(x1,y1),⋅⋅⋅,(xn−1,yn−1)}

使得对 k=0,1,⋅⋅⋅,n−1 ，所有 xk 各不相同

yk=A(xk)

多项式乘法

系数表达式的多项式乘法咱们已经很熟悉了，就是将两个多项式相乘然后合并同类项，时间复杂度为 O(n) ，而如果使用点值表达式计算多项式乘法的话则可以在 O(n) 的复杂度内完成计算，假设有两个n次多项式

A(x)={(x0,A0),(x1,A1),⋅⋅⋅,(xn−1,An−1)}B(x)={(x0,B0),(x1,B1),⋅⋅⋅,(xn−1,Bn−1)}

则 A(x)∗B(x) 为

{(x0,A0B0),(x1,A1B1),⋅⋅⋅,(xn−1,An−1Bn−1)}

FFT

点值表达式比系数表达式计算多项式乘法快，这为我们提供了计算多项式乘法提供了新方法，先将多项式转换成点值表达式再用点值表达式计算多项式乘法，再将点值表达式转换成系数表达式得到结果，可以用下图来表示

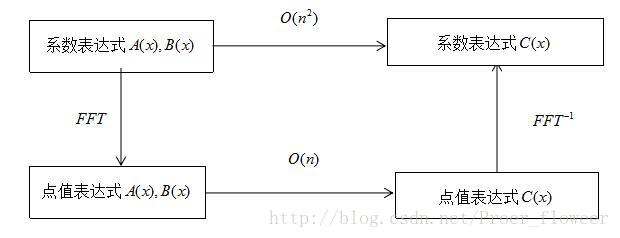
我们可以看到， FFT 就是将系数表达式转换成点值表达式的过程，点值表达式转换成系数表达式就是 FFT 的逆过程。
可以简单计算一下，如果随机取n个值，将系数表达式转换成点值表达式，复杂度为 O(n2) ，这和我们想要简化计算的需求相冲突，所以这里我们引入 n 次单位根来做序列来使转换可以折半递归计算，加速转换（涉及数学知识过多，不做过多赘述，有兴趣的朋友可以去看上面提供的博客，也可以翻阅算法导论第30章学习），使得 FFT 的时间复杂度为 O(nlog(n)) 。

FFT 模板

下面是hdu1402高精度乘法的题解代码，也可以作为 FFT 的模板使用。

#include 

using namespace std;

const double PI = acos(-1.0);

struct co{
    double r,i;
    co(double _r = 0.0,double _i=0.0){
        r = _r;
        i = _i;
    }
    co operator +(const co &b){
        return co(r+b.r,i+b.i);
    }
    co operator -(const co &b){
        return co(r-b.r,i-b.i);
    }
    co operator *(const co &b){
        return co(r*b.r-i*b.i,r*b.i+i*b.r);
    }
};

void change(co y[],int len){
    int i,j,k;
    for(int i = 1,j = len/2;i<len-1;i++){
        if(i < j){
            swap(y[i],y[j]);
        }
        k = len/2;
        while(j >= k){
            j -=k;
            k/=2;
        }
        if(j < k){
            j+=k;
        }
    }
}
void fft(co y[],int len,int on){
    change(y,len);
    for(int h = 2;h <=len;h<<=1){
        co wn(cos(-on*2*PI/h),sin(-on*2*PI/h));
        for(int j = 0;j < len;j+=h){
            co w(1,0);
            for(int k = j;k < j+h/2;k++){
                co u = y[k];
                co t = w*y[k+h/2];
                y[k] = u+t;
                y[k+h/2] = u-t;
                w = w*wn;
            }
        }
    }
    if(on == -1){
        for(int i = 0;i < len;i++){
            y[i].r /= len;
        }
    }
}

const int MAXN = 200010;
co x1[MAXN],x2[MAXN];
string str1,str2;
int sum[MAXN];

int main(){
    ios::sync_with_stdio(false);

    while(cin >> str1){
        cin >> str2;
        //cout << str1 << '\n' << str2 << '\n';
        int len1 = str1.length();
        int len2 = str2.length();
        int len = 1;
        while(len < len1*2||len < len2*2){
            len <<= 1;//为了迭代计算，点值表达式的长度须为2的整数次幂
        }
        for(int i = 0;i < len1;i++){
            x1[i] = co(str1[len1-1-i]-'0',0);
            sum[i] = 0;
        }
        for(int i = len1;i < len;i++){
            x1[i] = co(0,0);
            sum[i] = 0;
        }
        for(int i = 0;i < len2;i++){
            x2[i] = co(str2[len2-1-i]-'0',0);
        }
        for(int i = len2;i<len;i++){
            x2[i] = co(0,0);
        }
        fft(x1,len,1);
        fft(x2,len,1);
        for(int i = 0;i<len;i++){
            //cout << x1[i].r << ' ' << x2[i].r << '\n';
            x1[i] = x1[i]*x2[i];
        }
        fft(x1,len,-1);
        for(int i = 0;i < len;i++){
            sum[i] = (int)(x1[i].r+0.5);
            //cout << sum[i] << '\n';
        }
        for(int i = 0;i < len;i++){
            sum[i+1] += sum[i]/10;
            sum[i] %=10;
        }
        len = len1+len2-1;
        while(sum[len]<=0&&len>0){
            len--;
        }
        for(int i = len;i>=0;i--){
            cout << (char)(sum[i]+'0');
        }
        cout << '\n';
    }
    return 0;
}

需要注意的是如果多项式的次数不是2的整数次幂需要用系数0补齐至2的整数次幂，这样才能迭代计算，所以在使用时初始化也要注意，要将补齐部分也初始化。