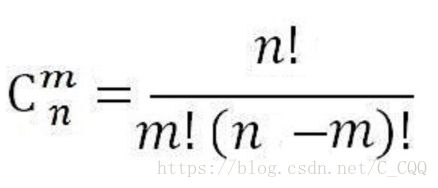7 组合数

组合数就是下面这样一个式子 

一、组合数

求组合数一般用杨辉三角性质，递推去求，但时间复杂度太高，还要取余

所以用逆元去求比较简单，根据上面的公式，需要求阶乘和逆元阶乘

代码如下：

const int N = 200000 + 5;
const int MOD = (int)1e9 + 7;
int F[N], Finv[N], inv[N];//F是阶乘，Finv是逆元的阶乘 
void init() {
    inv[1] = 1;
    for(int i = 2; i < N; i++) {
        inv[i] = (MOD - MOD / i) * 1ll * inv[MOD % i] % MOD;
    }
    F[0] = Finv[0] = 1;
    for(int i = 1; i < N; i ++) {
        F[i] = F[i-1] * 1ll * i % MOD;
        Finv[i] = Finv[i-1] * 1ll * inv[i] % MOD;
    }
}
int comb(int n, int m) {//comb(n, m)就是C(n, m) 
    if(m < 0 || m > n) return 0;
    return F[n] * 1ll * Finv[n - m] % MOD * Finv[m] % MOD;
}

二、大组合数 && 卢卡斯定理

当n和m很大时就要利用p

C(n, m) % p  =  C(n / p, m / p) * C(n%p, m%p) % p

对于C(n / p, m / p)，如果n / p 还是很大，可以递归下去

代码如下：

LL Lucas(LL n, LL m, int p) {
    return m ? Lucas(n / p, m / p, p) * comb(n % p, m % p, p) % p : 1;
}