数字图像处理笔记(十一):边缘检测算法
1 - 引言
在图像识别中,如果可以将图像感兴趣的物体或区别分割出来,无疑可以增加我们图像识别的准确率,传统的数字图像处理中的分割方法多数基于灰度值的两个基本性质
- 不连续性、
以灰度突变为基础分割一副图像,比如图像的边缘 - 相似性
根据一组预定义的准则将一副图像分割为相似的区域。阈值处理、区域生长、区域分裂和区域聚合都是这类方法的例子。
2 - 点、线和边缘检测基础
虽然许多检测算法都被opencv封装成函数可以直接调用,但是理解其背后的理论依据可以更好地帮助我们理解和改进算法
2.1 背景知识
- 一阶导数通常在图像中产生较粗的边缘;
- 二阶导数对精细细线,如细线、孤立点和噪声有较强的响应;
- 二阶导数在灰度斜坡和灰度台阶过渡出会产生双边响应;
- 二阶导数的符号可以用于确定边缘的过渡是从亮到暗还是从暗到亮
用于计算图像中每个像素位置处的一阶导数和二阶导数可选择方法是使用空间滤波器
R = w 1 z 1 + w 2 z 2 + ⋯ + w 9 z 9 = ∑ k = 1 9 w k z k R = w_1z_1+w_2z_2+\dots +w_9z_9=\sum_{k=1}^9w_kz_k R=w1z1+w2z2+⋯+w9z9=k=1∑9wkzk
2.1 - 孤立点的检测
点的检测以二阶导数为基础。这意味可以着使用拉普拉斯模板(详情见空间域滤波基础)
如果在某点该处模板的响应的绝对值超过了一个指定的阈值,那么我们` 说在模板中心位置(x,y)处的该点已被检测到了。在输入图像中,这样的点被标注为1,而所有其他点则被标注为0,从而产生一副二值图像。
g ( x , y ) = { 1 ∣ R ( x , y ) ∣ ≥ T 0 其他 g(x,y)=\begin{cases} 1& | R(x,y)| \geq T\\ 0 & \text{ 其他 } \end{cases} g(x,y)={10∣R(x,y)∣≥T 其他
其中,g是输出图像,T是一个非负的阈值,R由上式给出。
2.2 - 线检测
复杂度更高的检测是线检测,对于线检测,可以预期二阶导数将导致更强的响应,并产生比一阶导数更细的线。这样对于线检测,我们也可以使用拉普拉斯模板,记住,二阶导数的双线效应必须做适当的处理。

2.4 边缘模型
边缘检测是基于灰度突变来分割图像最常用的方法。我们从介绍一些边缘建模的方法开始,然后讨论一些边缘检测的方法。

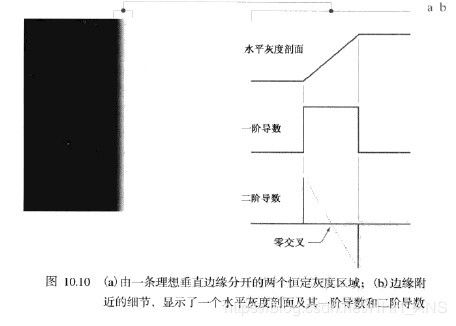
实际中,数字图像都存在被模糊且带有噪声的边缘,模糊程度主要取决于聚焦机理中的兼职,而噪声水平主要取决于成像系统的电子元件。在这种情况下,边缘被建模为一个更接近灰度斜坡的剖面。
并且我们可以得出结论:一阶导数的幅度可用于检测图像中的某个点是否存在一个边缘,二阶导数可以用于确定一个边缘像素位于该边缘的暗的一侧还是亮的一侧。
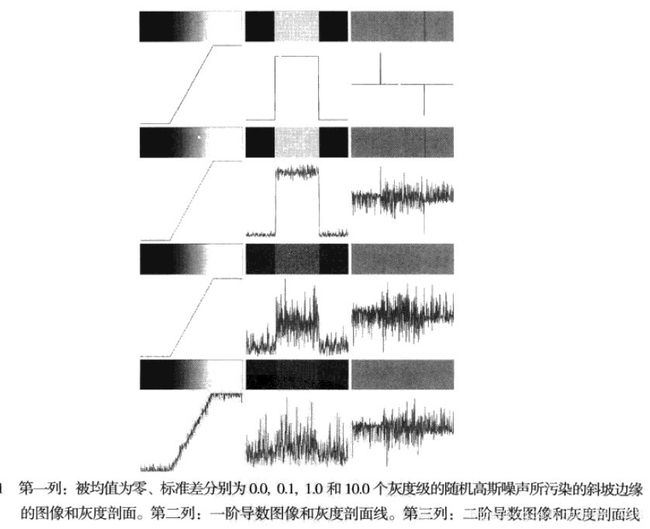
那么这是理想情况下的图片边缘,如果图片有噪声的话,其边缘函数则为
微弱的可见噪声对检测边缘所用的两个关键导数的严重影响的这一事实,是我们应记住的一个重要问题。特别地,在类似于我们刚刚讨论的水平的噪声很可能存在的应用中,使用导数之前的图像平滑处理是应该认真考虑的问题。
因此边缘检测的三个基本步骤
- 为降噪对图像进行平滑处理
- 边缘点的检测
- 边缘定位
2.4.1 - 基本的边缘检测算子
Roberts算子
Roberts算子以求对角像素之差为基础,该算子用于识别对角线方向的边缘:
g x = ( z 9 − z 5 ) 和 g y = ( z 8 − z 6 ) g_x=(z_9-z_5)和g_y=(z_8-z_6) gx=(z9−z5)和gy=(z8−z6)
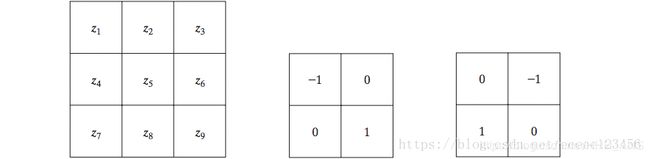
Prewitt算子
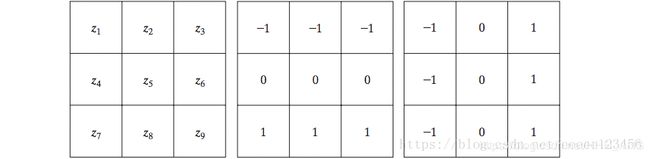
Prewitt算子使用以 z 5 z_5 z5为中心的3x3领域对 g x g_x gx和 g y g_y gy的近似如下式所示
g x = ( z 7 + z 8 + z 9 ) − ( z 1 + z 2 + z 3 ) g_x=(z_7+z_8+z_9)-(z_1+z_2+z_3) gx=(z7+z8+z9)−(z1+z2+z3)
g y = ( z 3 + z 6 + z 9 ) − ( z 1 + z 4 + z 7 ) g_y=(z_3+z_6+z_9)-(z_1+z_4+z_7) gy=(z3+z6+z9)−(z1+z4+z7)
模板如下图:
Sobel算子
Sobel算子使用以 z 5 z_5 z5为中心的3x3领域对 g x g_x gx和 g y g_y gy的近似如下式所示:
g x = ( z 7 + 2 z 8 + z 9 ) − ( z 1 + 2 z 2 + z 3 ) g_x=(z_7+2z_8+z_9)-(z_1+2z_2+z_3) gx=(z7+2z8+z9)−(z1+2z2+z3)
g y = ( z 3 + 2 z 6 + z 9 ) − ( z 1 + 2 z 4 + z 7 ) g_y=(z_3+2z_6+z_9)-(z_1+2_z4+z_7) gy=(z3+2z6+z9)−(z1+2z4+z7)
Sobel模板能较好地抑制(平滑)噪声地特性使得它更为可取,因为在处理导数时噪声抑制是一个重要地问题。 
检测对角边缘的Prewitt和Sobel模板
3 - 成熟先进的边缘检测技术
3.1 - Marr-Hildreth边缘检测器
① 概念背景:
最早的成功地尝试将更高级的分析结合到边缘检测处理之一应归功与Marr和Hildreth[1980]。
Marr和Hildreth证明了:
- 灰度边缘与图像尺寸无关,因此他们的检测要求使用不同尺寸的算子;
- 灰度的突然变化会在一阶导数中引起波峰或波谷,或在二阶导数中等效地引起零交叉
这些概念建议,用于边缘检测的算子应有两个显著的特点。
- 第一个和最重要的特点是它应该是一个能计算图像中每一点处的一阶导数或二阶导数的数字近似的微分算子。
- 第二个是它应能被“调整”以便在任何期望的尺寸上起作用
因此,大的算子也可以用于检测模糊边缘,小的算子也可以用于检测锐度集中的精细细节。
② 高斯拉普拉斯(LoG):
Marr和Hildreth证明了:满足这些最令人满意的算子是滤波器 ▽ 2 G \triangledown^2G ▽2G, ▽ 2 \triangledown^2 ▽2是拉普拉斯算子( ∂ 2 / ∂ x 2 + ∂ 2 / ∂ y 2 \partial^2/\partial x^2+\partial^2/\partial y^2 ∂2/∂x2+∂2/∂y2),而G是标准差为 σ \sigma σ的二维高斯函数
G ( x , y ) = e − x 2 + y 2 2 σ 2 G(x,y)=e^{-\frac{x^2+y^2}{2\sigma^2}} G(x,y)=e−2σ2x2+y2
为求 ▽ 2 G \triangledown^2G ▽2G的表达式,我们执行如下微分:
▽ 2 G ( x , y ) = ∂ 2 G ( x , y ) ∂ x 2 + ∂ 2 G ( x , y ) ∂ y 2 = ∂ ∂ x [ − x σ 2 e − x 2 + y 2 2 σ 2 ] + ∂ ∂ y [ − y σ 2 e − x 2 + y 2 2 σ 2 ] \triangledown^2G(x,y)=\frac{\partial^2G(x,y)}{\partial x^2}+\frac{\partial^2G(x,y)}{\partial y^2}=\frac{\partial}{\partial x}[\frac{-x}{\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}]+\frac{\partial}{\partial y}[\frac{-y}{\sigma^2}e^{-\frac{x^2+y^2}{2\sigma^2}}] ▽2G(x,y)=∂x2∂2G(x,y)+∂y2∂2G(x,y)=∂x∂[σ2−xe−2σ2x2+y2]+∂y∂[σ2−ye−2σ2x2+y2]
整理各项后给出如下最终表达式:
▽ 2 G ( x , y ) = [ x 2 + y 2 − 2 σ 2 σ 4 ] e − x 2 + y 2 2 σ 2 \triangledown^2G(x,y)=[\frac{x^2+y^2-2\sigma^2}{\sigma^4}]e^{-\frac{x^2+y^2}{2\sigma^2}} ▽2G(x,y)=[σ4x2+y2−2σ2]e−2σ2x2+y2
该表达式成为高斯拉普拉斯(LoG)
③ Marr-Hildreth算法
Marr-Hildreth算法由LOG滤波器与一副输入图像f(x,y)卷积组成,即
g ( x , y ) = [ ▽ 2 G ( x , y ) ] ★ f ( x , y ) g(x,y)=[\triangledown^2G(x,y)]\bigstar f(x,y) g(x,y)=[▽2G(x,y)]★f(x,y)
然后找寻g(x,y)的零交叉来确定f(x,y)中边缘的位置。因为这些都是线性操作,故可以写为
KaTeX parse error: Expected 'EOF', got '\bigstarf' at position 30: …ledown^2[G(x,y)\̲b̲i̲g̲s̲t̲a̲r̲f̲(x,y)]
它指出我们可以先使用一个高斯滤波器来平滑图像,然后计算该结果的拉普拉斯。
Marr-Hildreth算法小结
- 用一个G(x,y)取样得到的nxn的高斯高斯低通滤波器对输入图像滤波。
- 计算由第一步得到的图像的拉普拉斯
- 找到步骤2所有图像的零交叉
零交叉是Marr-Hildreth边缘检测方法的关键特征,实现简单,并且通常能给出好的结果。
import numpy as np
import matplotlib.pyplot as plt
import cv2
def edgesMarrHildreth(img, sigma):
"""
finds the edges using MarrHildreth edge detection method...
:param im : input image
:param sigma : sigma is the std-deviation and refers to the spread of gaussian
:return:
a binary edge image...
"""
size = int(2 * (np.ceil(3 * sigma)) + 1)
x, y = np.meshgrid(np.arange(-size / 2 + 1, size / 2 + 1), np.arange(-size / 2 + 1, size / 2 + 1))
normal = 1 / (2.0 * np.pi * sigma ** 2)
kernel = ((x ** 2 + y ** 2 - (2.0 * sigma ** 2)) / sigma ** 4) * np.exp(
-(x ** 2 + y ** 2) / (2.0 * sigma ** 2)) / normal # LoG filter
kern_size = kernel.shape[0]
log = np.zeros_like(img, dtype=float)
# applying filter
for i in range(img.shape[0] - (kern_size - 1)):
for j in range(img.shape[1] - (kern_size - 1)):
window = img[i:i + kern_size, j:j + kern_size] * kernel
log[i, j] = np.sum(window)
log = log.astype(np.int64, copy=False)
zero_crossing = np.zeros_like(log)
# computing zero crossing
for i in range(log.shape[0] - (kern_size - 1)):
for j in range(log.shape[1] - (kern_size - 1)):
if log[i][j] == 0:
if (log[i][j - 1] < 0 and log[i][j + 1] > 0) or (log[i][j - 1] < 0 and log[i][j + 1] < 0) or (
log[i - 1][j] < 0 and log[i + 1][j] > 0) or (log[i - 1][j] > 0 and log[i + 1][j] < 0):
zero_crossing[i][j] = 255
if log[i][j] < 0:
if (log[i][j - 1] > 0) or (log[i][j + 1] > 0) or (log[i - 1][j] > 0) or (log[i + 1][j] > 0):
zero_crossing[i][j] = 255
# plotting images
fig = plt.figure()
a = fig.add_subplot(1, 2, 1)
imgplot = plt.imshow(log, cmap='gray')
a.set_title('Laplacian of Gaussian')
a = fig.add_subplot(1, 2, 2)
imgplot = plt.imshow(zero_crossing, cmap='gray')
string = 'Zero Crossing sigma = '
string += (str(sigma))
a.set_title(string)
plt.show()
return zero_crossing
img = cv2.imread('images/17.jpg',0)
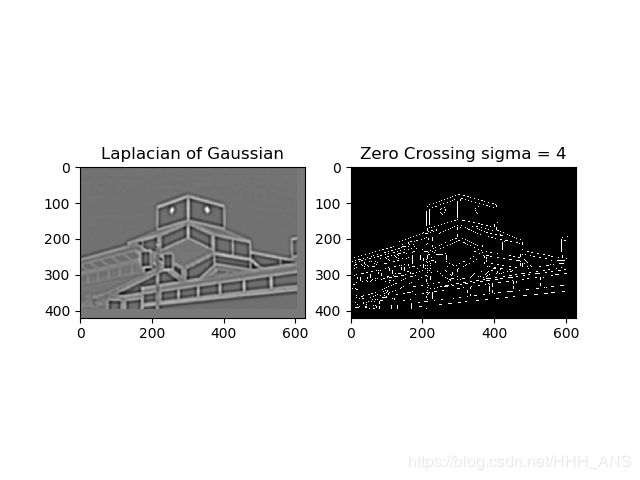
img = edgesMarrHildreth(img,4)
(可以看到这个算法检测出了图像的边缘,但是有很多地方都是不连续的,那么之后我们会介绍如何检测边界和边缘连接)
3.2 - 坎尼边缘检测(Canny)
虽然其算法更为复杂,但是Canny边缘检测是迄今为止讨论过的边缘检测器中最为优秀的,Canny基于三个基本目标:
- 低错误率。所有边缘都应被找到,并且应该没有伪相应,也就是检测到的边缘必须尽可能是真是的边缘
- 边缘点应被很好的定位。已定位边缘必须尽可能接近真实边缘。也就是由检测器标记为边缘的点和真实边缘的中心之间的距离应该最小
- 单一的边缘点响应。对于真实的边缘点,检测器仅应返回一个点。也就是真是边缘周围的局部最大数应该是最小的。这意味着在仅存一个单一边缘点到额位置,检测器不应指出多个边缘像素。
Canny工作的本质是,从数学上表达前面的三个准则,并试图找到这些表达式的最佳解,通常这是很困难的,但是我们可以使用高斯近似得出最优解:首先使用一个环形二维高斯函数平滑图像,计算结果的梯度,然后使用梯度幅度和方向来估计每一点的边缘强度与方向
第一步
令f(x,y)表示输入图像,G(x,y)表示高斯函数:
G ( x , y ) = e − x 2 + y 2 2 σ 2 G(x,y)=e^{-\frac{x^2+y^2}{2\sigma^2}} G(x,y)=e−2σ2x2+y2
我们用G和f卷积形成一幅平滑的图像 f s ( x , y ) f_s(x,y) fs(x,y):
f s ( x , y ) = G ( x , y ) ★ f ( x , y ) f_s(x,y)=G(x,y)\bigstar f(x,y) fs(x,y)=G(x,y)★f(x,y)
第二步
接下来计算结果的梯度幅度和方向:
M ( x , y ) = g x 2 + g y 2 M(x,y)=\sqrt {g_x^2+g_y^2} M(x,y)=gx2+gy2
α ( x , y ) = a r c t a n [ g y g x ] \alpha(x,y)=arctan[\frac{g_y}{g_x}] α(x,y)=arctan[gxgy]
第三步
细化边缘,使用非最大抑制:
- 寻找最接近 α ( x , y ) \alpha(x,y) α(x,y)的方向 d k d_k dk
- 若 M ( x , y ) M(x,y) M(x,y)的值至少小于沿 d k d_k dk的两个零邻居之一,零 g N ( x , y ) = 0 g_N(x,y)=0 gN(x,y)=0(抑制);否则令 g N ( x , y ) = M ( x , y ) g_N(x,y) = M(x,y) gN(x,y)=M(x,y),得到最大非抑制后的图像 g N ( x , y ) g_N(x,y) gN(x,y)
第四步
最后操作时对 g N ( x , y ) g_N(x,y) gN(x,y)进行阈值处理,以便减少伪边缘点,Canny算法使用两个阈值:低阈值 T L T_L TL和高阈值 T H T_H TH(Canny建议高低阈值比为2:1或3:1)
g N H = { g N ( x , y ) ≥ T H } g_{NH}=\left \{ g_N(x,y)\geq T_H\right\} gNH={gN(x,y)≥TH}
g N L = { g N ( x , y ) ≥ T L } g_{NL}=\left \{ g_N(x,y)\geq T_L\right\} gNL={gN(x,y)≥TL}
g N H = g N L ( x , y ) − g N H ( x , y ) g_{NH}= g_{NL}(x,y)-g_{NH}(x,y) gNH=gNL(x,y)−gNH(x,y)
g N H ( x , y ) g_{NH}(x,y) gNH(x,y)和 g N L ( x , y ) g_{NL}(x,y) gNL(x,y)的非零像素可分别视为“强”和“弱”边缘像素。其中 g N H ( x , y ) g_{NH}(x,y) gNH(x,y)为边缘点, g N L ( x , y ) g_{NL}(x,y) gNL(x,y)为候选点,对于候选点,如果与边缘点邻近,就标记为边缘点。
具体步骤如下:
- 在 g N H ( x , y ) g_{NH}(x,y) gNH(x,y)中定位一下个未被访问的边缘像素p
- g N L ( x , y ) g_{NL}(x,y) gNL(x,y)中与p是8邻接的像素标记为有效边缘像素
- 若 g N H ( x , y ) g_{NH}(x,y) gNH(x,y)中的所有非零像素已被访问,则跳到步骤4,否走返回步骤1
- 将 g N L ( x , y ) g_{NL}(x,y) gNL(x,y)中未标记为有效边缘像素的所有像素置零
在这一过程的末尾,将来自 g N L ( x , y ) g_{NL}(x,y) gNL(x,y)的所有非零像素附近到 g N H ( x , y ) g_{NH}(x,y) gNH(x,y),用Canny算子形成最终的输出图像。
那么我们来总结一下Canny算法
Canny算法步骤
- 用一个高斯滤波器平滑输入图像
- 计算梯度幅度图像和角度图像
- 对梯度幅度图像应用非最大抑制
- 用双阈值处理和连接分析来检测并连接边缘(这相对Marr-Hildreth优化了边缘的连接使得检测的边缘更加完整)
OpenCV将这一算法封装成了一个函数
def Canny(image, threshold1, threshold2, edges=None, apertureSize=None, L2gradient=None): # real signature unknown; restored from __doc__
"""
Canny(image, threshold1, threshold2[, edges[, apertureSize[, L2gradient]]]) -> edges
. @brief Finds edges in an image using the Canny algorithm @cite Canny86 .
.
. The function finds edges in the input image and marks them in the output map edges using the
. Canny algorithm. The smallest value between threshold1 and threshold2 is used for edge linking. The
. largest value is used to find initial segments of strong edges. See
.
.
. @param image 8-bit input image.
. @param edges output edge map; single channels 8-bit image, which has the same size as image .
. @param threshold1 first threshold for the hysteresis procedure.
. @param threshold2 second threshold for the hysteresis procedure.
. @param apertureSize aperture size for the Sobel operator.
. @param L2gradient a flag, indicating whether a more accurate \f$L_2\f$ norm
. \f$=\sqrt{(dI/dx)^2 + (dI/dy)^2}\f$ should be used to calculate the image gradient magnitude (
. L2gradient=true ), or whether the default \f$L_1\f$ norm \f$=|dI/dx|+|dI/dy|\f$ is enough (
. L2gradient=false ).
必要参数:
- 第一个参数是需要处理的原图像,该图像必须为单通道的灰度图;
- 第二个参数是阈值1;
- 第三个参数是阈值2。
函数返回一副二值图,其中包含检测出的边缘。
使用
Canny函数的使用很简单,只需指定最大和最小阈值即可。如下:
# coding=utf-8
import cv2
import numpy as np
img = cv2.imread("images/17.jpg", 0)
cv2.imshow('img',img)
img = cv2.GaussianBlur(img, (3, 3), 0)
canny = cv2.Canny(img, 50, 150)
cv2.imshow('Canny', canny)
cv2.waitKey(0)
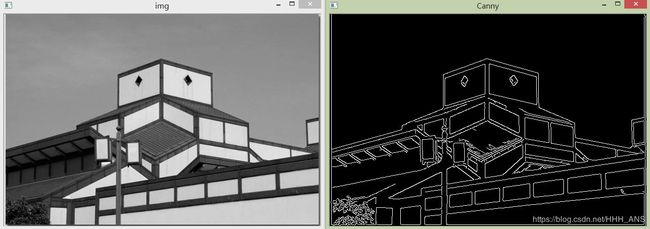
cv2.destroyAllWindows()
可以看到,Canny算法明显提取边缘的效果要优于Marr-Hildreth算法,对边缘的连接也做的更好。