数字图像处理笔记（十二）：图像分割算法

1 - 引言

在图像识别中，如果可以将图像感兴趣的物体或区别分割出来，无疑可以增加我们图像识别的准确率，传统的数字图像处理中的分割方法多数基于灰度值的两个基本性质

• 不连续性
  以灰度突变为基础分割一副图像，比如图像的边缘
• 相似性
  根据一组预定义的准则将一副图像分割为相似的区域。阈值处理、区域生长、区域分裂和区域聚合都是这类方法的例子。
  在边缘检测算法中我们学习了如何利用不连续性来分割图像。
  本文将从相似性这个角度，学习使用阈值处理、基于区域、和基于形态学的分水岭分割图像

2 - 阈值处理

由于阈值处理直观、实现简单且计算速度快，因此图像阈值处理在图像分割应用中处于核心地位

2.1 - 基础知识

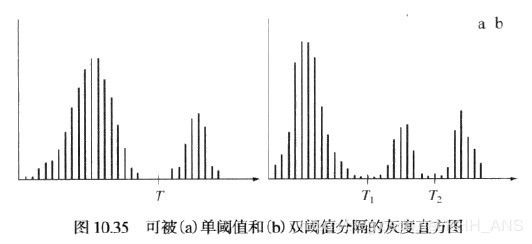
下图灰度直方图对应图像f(x,y)，然后f(x,y)>T的任何点(x,y)称为一个对象点；否则将该点称为背景点。分割后的图像g(x,y):
$$g(x,y)=\{\begin{array}{ll}1& f(x,y)>T\\ 0& f(x,y)\le T\end{array}$$

当T时一个适用于整个图像的常数时，该公式给出的处理称为全局阈值处理。

但是要求两个以上阈值的分割问题很难解决（通常是不可能的），而较好的结果通常可以用其他方法得到。

我们可以很自然的得出灰度阈值的成功与否直接关系到可区分的直方图模式的谷的宽度和深度，而影响波谷特性的关键因素是：

1. 波峰间的间隔（波峰离的越远，分离这些模式的机会越好）
2. 图像中的噪声内容（模式随噪声的增加而展宽）
3. 物体和背景的相对尺寸
4. 光源的均匀性
5. 图像反射特性的均匀性

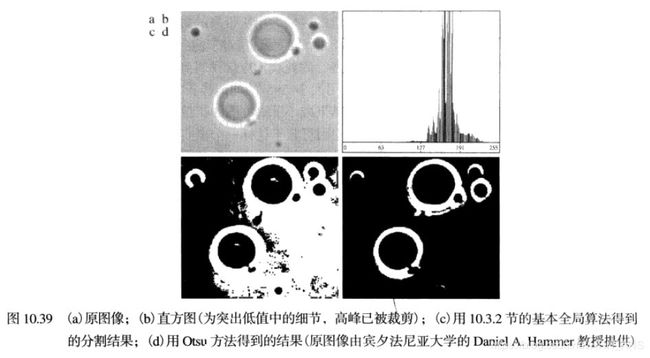
2.2 - 基本的全局阈值处理

在大多数应用中，通常图像之间有较大的变化，即使全局阈是一种合适的方法，对每一幅图像有能力自动估计阈值的算法也是需要的。下面的迭代算法可以用于这一目的：

1. 为全局阈值T选择一个初始估计值
2. 利用T分割图像。这将产生两组像素：$G_1$由灰度值大于T的所有像素组成，$G_2$由所有小于等于T的像素组成。
3. 对$G_1$和$G_2$的像素分别计算平均灰度值（均值）$m_1$和$m_2$
4. 计算一个新的阈值：$$T=\frac{1}{2}(m_1+m_2)$$
5. 重复步骤2到步骤4，直到连续迭代中的T值间的差小于一个预定义的参数$\Delta T$为止
   

2.3 - 用Otsu方法的最佳全局阈值处理

阈值处理可视为一种统计决策理论问题，其目的是在把像素分配给两个或多组（也称分类）的过程中引入的平均误差最小。Otsu方法（Otsu[1979]）是另一种有吸引力的方案。

Otsu方法有一个重要的特性，即它完全以在一幅图像的直方图上执行计算为基础。

一幅图像有MxN个像素，L个不同的灰度级，$n_i$表示灰度级为i的像素个数。那么图像中像素总数MN为$MN=n_0+n_1+\cdots +n_{L-1}$

归一化的直方图$p_i=n_i/MN$，由此有
$$\sum _{i=0}^{L-1}{p}_i=1,p_i\ge 0$$

现在，我们假设选择一个阈值$T(k)=k,0<k<L-1$，并使用它把输入图像阈值化处理为两类$C_1$和$C_2$，其中，$C_1$由图像中灰度值在范围[0,k]内的所有像素组成，$C_2$由灰度值在范围[k+1,L-1]内的所有像素组成。用该阈值，像素被分到类$C_1$中的概率$P_1(k)$由如下的积累和给出：
$$P_1(k)=\sum _{i=0}^k{p}_i$$

因此分配到$C_1$的像素的平均灰度值为：
$$m_1(k)=\sum _{i=0}^{k}iP(i/C_1)$$
$$=\sum _{i=0}^{k}iP(C_1/i)P(i)/P(C_1)$$
$$=\frac{1}{P_1(k)}\sum _{i=0}^{k}iP(i)$$

第二行来自贝叶斯公式：
$$P(A/B)=P(B/A)P(A)/P(B)$$

类似的我们也可以得到$C_2$的像素平均灰度值

然后我们可以得到整个图像的平均灰度值
$$m_G=\sum _{i=0}^{L-1}iP(i)$$

为了评价阈值K的“质量”，我们使用归一化的无量纲矩阵

$$\eta =\frac{{\sigma }_B^2}{{\sigma }_G^2}$$

其中，${\sigma }_G^2$是全局方差[即图像中所有像素的灰度方差]
$${\sigma }_G^2=\sum _{i=0}^{L-1}(i-mG{)}^2{p}_i$$

${\sigma }_B^2$为类间方差，它定义为
$${\sigma }_B^2=P_1(m_1-m_G{)}^2+P_2(m_2-m_G{)}^2$$
该表达式还可写为
$${\sigma }_B^2=P_1{P}_2(m_1-m_2{)}^2$$
$$=\frac{(m_G{P}_1-m{)}^2}{P_1(1-P_1)}$$

从上面公式可以看出，两个均值$m_1$和$m_2$彼此隔得越远，${\sigma }_B^2$越大，这表明类间方差是类之间的可分性度量。因为${\sigma }_G^2$是一个常数，由此得出$\eta$也是一个可分性度量，且最大化这一度量等价于最大化${\sigma }_B^2$。

一旦得到可以使${\sigma }_B^2(k^{\ast })$最大的$k^{\ast }$，便可以得到分割图像：
$$g(x,y)=\{\begin{array}{ll}1& f(x,y)>k^{\ast }\\ 0& f(x,y)\le k^{\ast }\end{array}$$

Otsu算法小结如下：

1. 计算输入图像的归一化直方图。使用$p_i,i=0,1,2,\dots ,L-1$表示该直方图的各个分量
2. 计算累积和$P_i(k)$
3. 计算累积均值$m(k)$
4. 计算全局灰度均值$m_G$
5. 计算类间方差${\sigma }_B^2(k)$
6. 得到Otsu阈值$k^{\ast }$，如果最大值不唯一，则使用平均值
7. 计算可分性度量${\eta }^{\ast }$
   

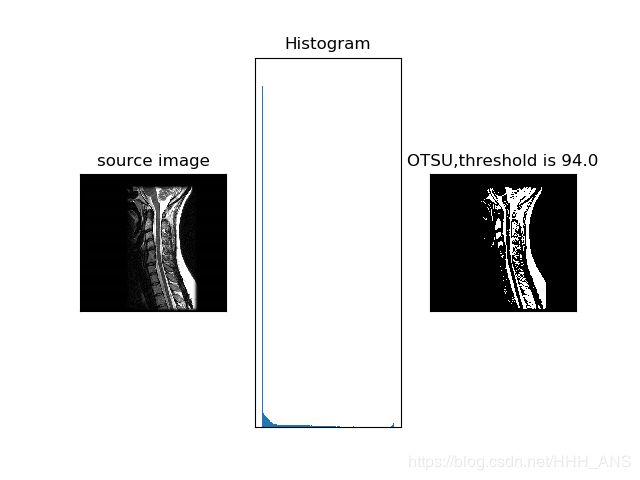
OpenCV同样将这一经典算法封装成了函数

#coding:utf-8
import cv2
import numpy as np
from matplotlib import pyplot as plt

image = cv2.imread("images/gamma.jpg")
gray = cv2.cvtColor(image, cv2.COLOR_BGR2GRAY)

plt.subplot(131), plt.imshow(image, "gray")
plt.title("source image"), plt.xticks([]), plt.yticks([])
plt.subplot(132), plt.hist(image.ravel(), 256)
plt.title("Histogram"), plt.xticks([]), plt.yticks([])
ret1, th1 = cv2.threshold(gray, 0, 255, cv2.THRESH_OTSU)  #方法选择为THRESH_OTSU
plt.subplot(133), plt.imshow(th1, "gray")
plt.title("OTSU,threshold is " + str(ret1)), plt.xticks([]), plt.yticks([])
plt.show()

2.4 - 用图像平滑改善全局阈值处理

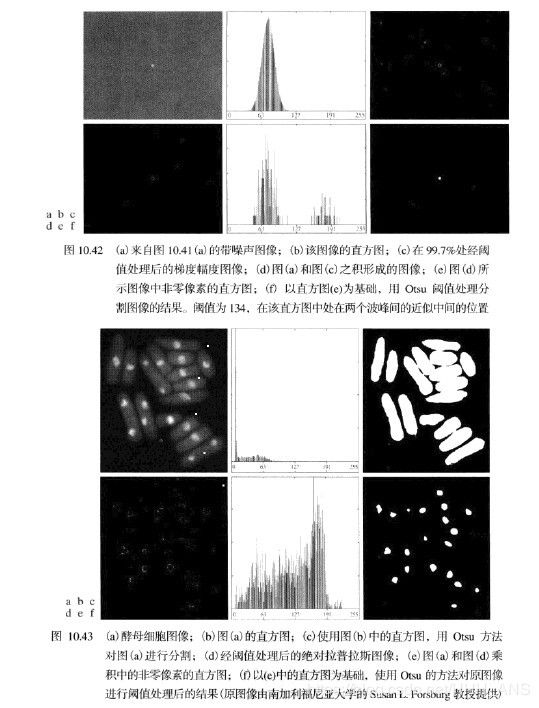
噪声会将简单的阈值处理问题变为不可解决的问题。当噪声不能在源头减少，并且阈值处理又是所选择的分割方法时，通常能增强性能的一种技术是，在阈值处理之前平滑图像。
经平滑和分割后的图像，由于对边界的模糊，会造成物体和背景间的边界稍微有点失真。对一幅图像平滑越多，分割后的结果中的边界误差就越大。

2.5 - 利用边缘改进全局阈值处理

f(x,y) 表示输入图像，利用边缘改进全局阈值处理算法如下：

1. 采用特征检测中讨论的任何一种方法来计算一幅边缘图像，无论是 f(x,y) 梯度的幅度还是拉普拉斯的绝对值均可。
2. 指定一个阈值 T。
3. 用步骤2中的阈值对步骤1中的图像进行阈值处理，产生一幅二值图像 $g_T(x,y)$
   ​在从 f(x,y) 中选取对应于“强”边缘像素的下一步中，该图像用做一幅模板图像。
4. 仅用 f(x,y) 中对应于 $g_T(x,y)$中像素值为1的位置的像素计算直方图。

3 - 基于区域的分割

3.1 - 区域生长

区域生长的基本方法是从一组“种子”点开始，将于种子预先定义的性质相似的那些领域像素添加到每个种子上来形成这些生长区域（如特定范围的灰度或颜色）

令f(x,y)表示一个输入图像阵列；S(x,y)表示一个种子陈列，陈列中种子点位置处为1，其他位置处为0；Q表示在每个位置（x,y）所用的属性。假设陈列f和s的尺寸相同。基于8连接的一个基本区域生长算法可以说明如下：

1. 在S(x,y)中寻找所有连通分量，并把每个连通分量腐蚀为一个像素；把找到的所有这种像素标记为1，把S中的所有其他像素标记为0
2. 在坐标对（x,y）处形成图像$f_Q$:如果输入图像在该坐标处满足给定的属性Q，则令$f_Q(x,y)=1$，否则令$f_Q(x,y)=0$
3. 令g是这样形成的图像：把$f_Q$中未8连通种子的所有1值点，添加到S中的每个种子店
4. 用不同的区域标记标记处g中的每个连通分量。区域生长得到的分割图像

import numpy as np
import cv2

class Point(object):
    def __init__(self,x,y):
        self.x = x
        self.y = y

    def getX(self):
        return self.x
    def getY(self):
        return self.y

def getGrayDiff(img,currentPoint,tmpPoint):
    return abs(int(img[currentPoint.x,currentPoint.y]) - int(img[tmpPoint.x,tmpPoint.y]))

def selectConnects(p):
    if p != 0:
        connects = [Point(-1, -1), Point(0, -1), Point(1, -1), Point(1, 0), Point(1, 1), \
                    Point(0, 1), Point(-1, 1), Point(-1, 0)]
    else:
        connects = [ Point(0, -1),  Point(1, 0),Point(0, 1), Point(-1, 0)]
    return connects

def regionGrow(img,seeds,thresh,p = 1):
    height, weight = img.shape
    seedMark = np.zeros(img.shape)
    seedList = []
    for seed in seeds:
        seedList.append(seed)
    label = 1
    connects = selectConnects(p)
    while(len(seedList)>0):
        currentPoint = seedList.pop(0)

        seedMark[currentPoint.x,currentPoint.y] = label
        for i in range(8):
            tmpX = currentPoint.x + connects[i].x
            tmpY = currentPoint.y + connects[i].y
            if tmpX < 0 or tmpY < 0 or tmpX >= height or tmpY >= weight:
                continue
            grayDiff = getGrayDiff(img,currentPoint,Point(tmpX,tmpY))
            if grayDiff < thresh and seedMark[tmpX,tmpY] == 0:
                seedMark[tmpX,tmpY] = label
                seedList.append(Point(tmpX,tmpY))
    return seedMark


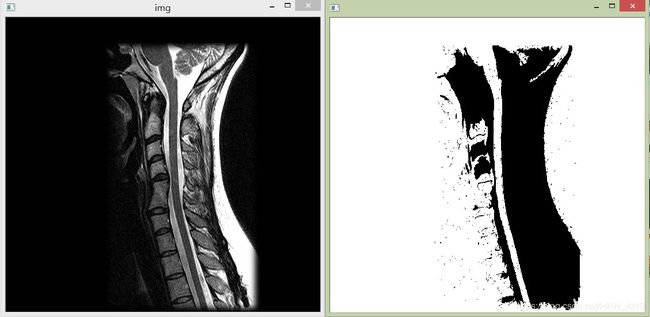
img = cv2.imread('images/gamma.jpg',0)
seeds = [Point(10,10),Point(82,150),Point(20,300)]
binaryImg = regionGrow(img,seeds,10)
cv2.imshow('img',img)
cv2.imshow(' ',binaryImg)
cv2.waitKey(0)

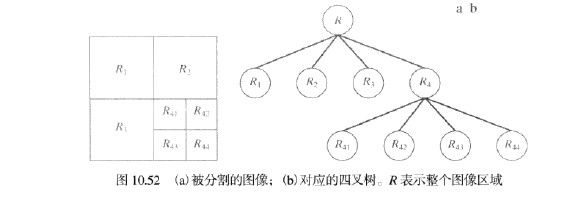
3.2 - 区域分裂与聚合

这种方法是将一幅图像细分为一组任意不相交区域，然后聚合和/或分裂这些区域。

可总结为：

1. 对满足Q（R_i）=FALSE的任何区域$R_i$分裂为4个不相交的象限区域
2. 当不可能进一步分裂时，对满足条件$Q(R_j\cup R_k)=TRUE$的任意两个邻接区域$R_j$和$R_k$进行聚合
3. 当无法进一步聚合时，停止操作

习惯上要规定一个不能再进一步执行分裂的最小四象限的尺寸

4 - 基于形态学分水岭的分割

4.1 - 背景知识

形态学分水岭分割将前面讨论的分割方法中的许多概念进行了具体化，因此通常会产生更稳定的分割结果，包括连接的分割边界。
分水岭的概念是以三维方式来形象化一幅图像为基础的：两个空间坐标作为灰度的函数，如图2所示。在这种“地形学”解释中，我们考虑三种类型的点：

1. 属于一个区域最小值的点；
2. 把一点视为一个水滴，如果把这些点放在任意位置上，水滴一定会下落到某个最小值点；
3. 处在该点的水会等概率地流向不止一个这样的最小值点。
   对于一个特定的区域最小值，满足条件(b)的最小值点的集合称为该最小值的汇水盆地或分水岭。满足条件(3)的点形成地面的峰线，它称为分割线或分水线。

4.2 - 分水岭分割算法

令$M_1,M_2,\dots ,M_R$是地图图像$g(x,y)$中区域最小值点的坐标集。令$C(M_i)$是与区域最小值$M_i$相关的汇水盆地中的点的坐标集，符号$min$和$max$表示$g(x,y)$的最小值和最大值，最后令$T[n]$表示满足$g(s,t)<n$的坐标(s,t)的集合，即：
KaTeX parse error: Expected 'EOF', got '\right' at position 6: T[n]=\̲r̲i̲g̲h̲t̲\{(s,t)|g(s,t)<…
令$C_n(M_i)$表示汇水盆地中与淹没阶段n的最小值$M_i$相关联的点的坐标集，即：
$$C_n(M_i)=C(M_i)\bigcap T[n]$$
接下来，令$C[n]$表示阶段n中已被水淹没的汇水盆地的并集：
$$C[n]=\bigcup _{i=1}^R{C}_n(M_i)$$
然后，令$C[max+1]$表示所有汇水盆地的并集：
$$C[max+1]=\bigcup _{i=1}^{R}C(M_i)$$
寻找分水先的算法使用$C[min+1]=T[min+1]$来初始化，然后，该算法进行递归处理，由$C[n-1]$计算$C[n-1]$计算$C[n]$
由$C[n-1]$求得$C[n]$过程如下：令Q表示$T[n]$中的连通分量的集合，然后对于每个连通分量$q\in Q[n]$，有如下三种可能性：

1. $q\bigcap C[n-1]$为空集
2. $q\bigcap C[n-1]$包含$C[n-1]$的一个连通分量
3. $q\bigcap C[n-1]$包含$C[n-1]$的一个以上的连通分量

由 $C[n-1]$构建$ C[n]$取决于这三个条件中的哪个条件成立。遇到一个新的最小值时，条件1发生，这种情况下，连通分量$ q $并入 $C[n-1]$中形成$ C[n]$。当q位于某些局部最小值的汇水盆地内时，条件2发生，这种情况下，q并入$ C[n−1]$中形成 $C[n] $。
当遇到全部或部分分隔两个或多个汇水盆地的山脊线时，条件3发生。进一步淹没会导致这些汇水盆地中的水位聚合。因此，必须在 q 内构筑一个水坝（如果涉及两个以上的汇水盆地，就要构筑多个水坝）以阻止汇水盆地间的水溢出。

import numpy as np
import cv2
from matplotlib import pyplot as plt

img = cv2.imread('images/1.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
ret, thresh = cv2.threshold(gray,0,255,cv2.THRESH_BINARY_INV+cv2.THRESH_OTSU)


# noise removal
kernel = np.ones((3,3),np.uint8)
opening = cv2.morphologyEx(thresh,cv2.MORPH_OPEN,kernel, iterations = 2) # 形态开运算

# sure background area
sure_bg = cv2.dilate(opening,kernel,iterations=3)

# Finding sure foreground area
dist_transform = cv2.distanceTransform(opening,cv2.DIST_L2,5)
ret, sure_fg = cv2.threshold(dist_transform,0.7*dist_transform.max(),255,0)

# Finding unknown region
sure_fg = np.uint8(sure_fg)
unknown = cv2.subtract(sure_bg,sure_fg)


# Marker labelling
ret, markers = cv2.connectedComponents(sure_fg)

# Add one to all labels so that sure background is not 0, but 1
markers = markers+1

# Now, mark the region of unknown with zero
markers[unknown==255] = 0

markers = cv2.watershed(img,markers)
img[markers == -1] = [255,0,0]


cv2.imshow('img',img)
cv2.waitKey(0)
cv2.destroyAllWindows()