bzoj 1856（组合数学）

传送门
题解：答案是C(n+m,m)-C(n+m,m-1)。C(n+m,m)是总方案数（n+m个位置中选m个放0），然后减去不合法的。将题意转化为：从一个矩阵的左下走到右上不能经过某条水平直线的方案数。
如果我们把1看作一个向量（1,1）,0看作一个向量（1,-1），那问题就转化成从（0,0）走到（n+m,n-m）不经过直线y=-1的方案数。考虑限制的话，我们看图发现经过y=-1的情况可以看作从（0,-2）出发到（n+m,n-m）的方案数，所以不合法的方案数是C(n+m,m-1)（原来能选m个0，但是现在起点纵坐标下降2个单位，所以只好少走一个0，多走一个1转化成m-1）

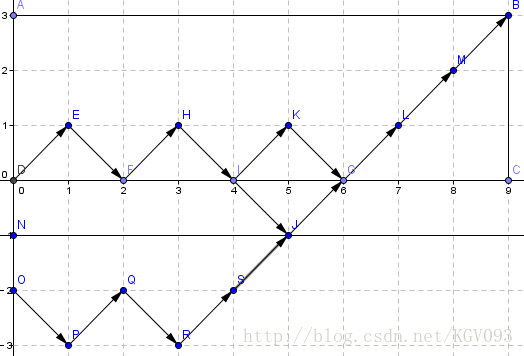
图片来自：http://blog.csdn.net/wzq_qwq/article/details/48706151

#include
using namespace std;
typedef long long ll;
const int MAXN=2e6+2;
const ll MOD=20100403;
int n,m,nm;
ll fac[MAXN]={1};
inline ll fpow(ll a,ll b,ll p) {
    ll ret=1;
    while (b) {
        if (b&1) ret=ret*a%p;
        b>>=1,a=a*a%p;
    }
    return ret;
}
inline ll comb(int n,int m) {
    return fac[n]*fpow(fac[n-m]*fac[m]%MOD,MOD-2,MOD)%MOD;
}
int main() {
    scanf("%d%d",&n,&m);
    nm=n+m;
    for (register int i=1;i<=nm;++i) fac[i]=fac[i-1]*i%MOD;
    printf("%lld\n",(comb(n+m,m)-comb(n+m,m-1)%MOD+MOD)%MOD);
    return 0;
}