SLAM笔记(四)运动恢复结构的几何数学(本征矩阵、单应矩阵、基础矩阵)
1. 间接法进行运动恢复的前提假设
对于结构与运动或视觉三维重建中,通常假设已经通过特征匹配等方法获取了匹配好的点对。
先求出匹配点对再获取结构和运动信息的方法称作间接法。
间接法最重要的三个假设是:
1.拥有一系列两帧之间的匹配点对。但同时假设匹配关系不一定精确:
- 匹配点不一定精确,即对于匹配点对 ( A n , A n + 1 ) (A_n,A_{n+1}) (An,An+1), A n + 1 A_{n+1} An+1可能并非 A n A_n An的真实匹配 点,而是在它周围;
- 匹配关系不一定正确。
2.场景是静态的,即环境中不存在运动的物体
3.知道相机内参数且内参数恒定不变
此处的匹配点,可以是2D-2D(单目相机初始化时),2D-3D配对点(单目相机运行过程中,已经算出了3D的地图点,又来了2D的图形),或是3D-3D的匹配点(使用双目相机、RGBD相机或其他传感器,可以直接过间接获取匹配好的三维点对)。本文讨论的主要是是基于2D-2D的配对点。
2.极线约束,本征矩阵
2.1 极线约束:
物理世界上的一个三维点P投影到两个成像面(实际上像面也常常处理成z=1的地方)上,点P与两个像面的光心形成一个对极平面, l 1 , l 2 l_1,l_2 l1,l2分别为对极平面与像平面相交的极线。
极线约束是指对第一个成像面上的点p1,它在第二个平面上的对应点p2总存在于对应的极线 l 2 l_2 l2上。
用 x x x表示像平面坐标的话, K K K为内参数矩阵,P为相机坐标系三维点;如果已知内参数 K K K,则可以去掉 K K K的影响,即令 x = K − 1 p x = K^{-1}p x=K−1p,得到
λ 1 x 1 = P , λ 2 x 2 = R P + T \lambda_1x_1 = P,\lambda_2x_2 = RP+T λ1x1=P,λ2x2=RP+T
即:
λ 2 x 2 = λ 1 R x 1 + T \lambda_2 x_2 = \lambda_1Rx_1+T λ2x2=λ1Rx1+T(2-1)
此处的 x 1 , x 2 x_1,x_2 x1,x2可以看做是 z = 1 z=1 z=1平面上的点。
2.1.1 极线约束(Epipolar constraint,essential constraint,bilinear constraint):
对于两帧之间的归一化坐标 x 1 , x 2 x_1,x_2 x1,x2,
x 2 T T ^ R x 1 = 0 , ( 2 − 1 ) x_2^T\hat TRx_1 = 0,(2-1) x2TT^Rx1=0,(2−1)
其推导过程如下:
1。由于 λ x = X \lambda x = X λx=X(相机坐标系下世界坐标),则可得:
![]()
R,T分别为旋转和平移矩阵。
2.左右分别左乘 T ^ \hat T T^,即得到
![]()
3.左乘 x 2 x_2 x2,除掉 λ \lambda λ影响:(将此缩放因子放入E中,此缩放因子在4部分会介绍),将上式左右两边投影到 x 2 x_2 x2上,即左乘上 x 2 T x_2^T x2T,左侧即为0(因为 T × x 2 垂 直 于 x 2 , 因 此 左 乘 x 2 即 为 0 T\times x_2垂直于x_2,因此左乘x_2即为0 T×x2垂直于x2,因此左乘x2即为0),得极线约束:
x 2 T T ^ R x 1 = 0 x_2^T\hat T Rx_1 = 0 x2TT^Rx1=0
注:
上述2,3过程中, T ^ , x 2 \hat T,x_2 T^,x2都是不可逆的,因此这两个投影都是不可逆投影(与下文的可逆投影–单应性不同);某种意义上这两个过程将强约束转化成弱约束了,但获得的好处是将二维点直接联系起来,不用考虑三维点。
2.1.2 极线约束的几何意义
![]()
x 1 , x 2 x_1,x_2 x1,x2分别为从光心发出的向量。由于T为光心之间连线的向量,三个向量共面,所以该triple product为0。
对于式$ x_2^TEx_1=0 , 如 果 令 ,如果令 ,如果令l=Ex_1$
( E x 1 Ex_1 Ex1结果为{a,b,c},对应于右侧像平面坐标上的直线ax+bx+c=0),则存在: x 2 T l = 0 x_2^Tl=0 x2Tl=0,即 x 2 x_2 x2存在于右侧极线l上
2.1.3 本征矩阵
令本征矩阵(Essential Matrix): E = T ^ R E = \hat TR E=T^R,则:
x 2 T E x 1 = 0 x_2^TEx_1 = 0 x2TEx1=0(2-2)
E组成的空间称为本征空间:
![]()
本征矩阵定义:
一个非零矩阵当且仅当(充要条件)svd 分解中 Σ \Sigma Σ是:
d i a g { a , a , 0 } , a > 0 diag \{a,a,0 \},a>0 diag{a,a,0},a>0
时,这个矩阵是本征矩阵。
为什么特征空间需要这样定义?
1.为什么秩为2?由于rank( R R R) = 3;rank( T × T_{\times} T×)=2,所以E为2。
2.为什么特征值相等?Since in the reconstruction, E is only defined up to a scalar
此时可由E求得R和T:
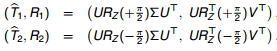
因此视觉SFM(structure of motion)问题中恢复分两步走:
- Recover the Essential Matrix frome the epipolar constraints
- Extract the R,T if we know the Essential Matrix:E=U σ \sigma σV
从一系列极线约束中恢复的矩阵E一般是不满足本征矩阵的条件的;怎么办,再将E投影到本征空间即可,具体做法是称为八点法。
3.运动信息重建(旋转和平移信息)
3.1 八点法(Eight-Point Algorithm)
3.1.1从点对中求解出矩阵E
先将矩阵E写作栈的形式:
![]()
同时,假设点的齐次向量 x 1 , x 2 x_1,x_2 x1,x2表示成如下形式:
![]()
![]()
则极线约束可换成两个向量乘积的形式:
x 2 T E x 1 = a T E S , ( 2 − 3 ) x_2^TEx_1 = a^TE^S,(2-3) x2TEx1=aTES,(2−3)
对于n个点对:上式为:
χ E S = 0 , w i t h χ = ( a 1 , a 2 , a 3 , . . . , a n ) T , ( 2 − 4 ) \chi E^S = 0,with \chi = (a^1,a^2,a^3,...,a^n)^T,(2-4) χES=0,withχ=(a1,a2,a3,...,an)T,(2−4)
因此求解E变成求解方程(2-3),即 χ \chi χ的零空间E。为了得到唯一解(除了平凡解E=0), χ \chi χ的秩应该是8。至少需要8个点对,即 χ \chi χ的列数为8,rank( χ \chi χ)才可能为8。当然,假如点对中某些点相互之间是线性相关,比如3个或以上的点在同一直线上,或者4个或以上点在同一平面上,则秩并非点对个数,此时需要8个以上的点才可能满足要求。
由于无法知道E的正负(方向),因此结合每个E有两个可能的(R,T)组合,最终可能有四个可能的(R,T)
3.1.2将矩阵E投影到本征空间中
由于用线性方法求解的 E E E往往不满足上部分2所要求的两个非零特征值相等的要求,因此需要将E做一些变换,也即将E投影到特征空间上,具体做法是:
对于
E = U d i a g { λ 1 , λ 2 , λ 3 } V T E = Udiag\{\lambda_1,\lambda_2,\lambda_3\}V^T E=Udiag{λ1,λ2,λ3}VT
投影到特征空间后为:
E p = U d i a g { σ , σ , 0 } V T , w i t h σ = ( λ 1 + λ 2 ) / 2 E_p = Udiag\{ \sigma,\sigma,0\}V^T,with\ \ \sigma = (\lambda_1+\lambda_2)/2 Ep=Udiag{σ,σ,0}VT,with σ=(λ1+λ2)/2
在三维重建中一般将 E p E_p Ep投影到归一化的特征空间上:即 E p = U d i a g { σ , σ , 0 } V T E_p = Udiag\{ \sigma,\sigma,0\}V^T Ep=Udiag{σ,σ,0}VT除以 σ \sigma σ,得到归一化的结果 E p = U d i a g { 1 , 1 , 0 } V T E_p = Udiag\{ 1,1,0\}V^T Ep=Udiag{1,1,0}VT。
**总结:**八点法(Longuet-Higgins ’81)的具体做法:
1.通过最小化 ∣ ∣ χ E s = 0 ∣ ∣ ||\chi E^s = 0|| ∣∣χEs=0∣∣计算近似的本征矩阵E;
2.SVD分解E,并E投影到特征空间,并将结果归一化
3.从特征矩阵中恢复出R,T:
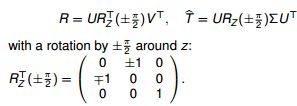
求出的四个(R,T)对的效果如下图所示:
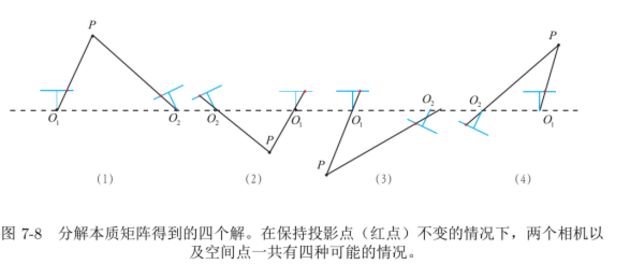
能看出四个(R,T)解中只有一个解是有意义的,只有这个解才能使所有点的深度是正的。
3.2 五点法(Five-Point Algorighm)
矩阵E的自由度:
由于E由三个旋转,三个位移构成,一共六个自由度;但由于 χ E = 0 \chi E = 0 χE=0中对于E乘上一个数 λ \lambda λ齐次式都成立,因此E实际自由度为5。
Kruppa 在 1913证明只需要5个匹配点对就能算出E,即五点法。
由于五点法引入了非线性约束,解起来麻烦,于是这儿就不详解了,只是大概表述如下:
χ ( p 1 E 1 + p 2 E 2 + p 3 + E 3 + p 4 E 4 ) = 0 \chi (p_1E_1+p_2E_2+p_3+E_3+p_4E_4) = 0 χ(p1E1+p2E2+p3+E3+p4E4)=0
如果有额外的信息,比如运动是在同一平面运动或绕圆周运动,又比如有了惯性传感器可以知道其他位姿信息,则需要更少的点就可以求出本征矩阵。
continuous epipolar constraint:产生线速度和角速度而非位移T和旋转R。
** independently moving objects:**
( x 2 T E 1 x 1 ) ( x 2 T E 2 x 1 ) = 0 (x_2^TE_1x_1)(x_2^TE_2x_1) = 0 (x2TE1x1)(x2TE2x1)=0(two independent motion)
3.3 单应性矩阵H
3.3.1 来自平面上的单应性
单应矩阵到底是个什么东西?
单应映射就是最普通的线性映射关系
当我们从两幅image上看到真实世界中的同一个有限平面(如一个长方形)时,假设长方形在image1中形成的投影为四边形1,在image2中形成的投影为四边形2;长方形任何一个点x在四边形1的对应的点x1,在四边形2中的对应点x2。
由长方形中的x不同可知这些二维点对 ( x 1 , x 2 ) (x1,x2) (x1,x2)有无数个,但我们可以用一个3x3的单应矩阵H来表示所有的对应关系: x 2 = H x 1 x2 = Hx1 x2=Hx1。为什么呢,因为他们都同属一个平面。
计算单应性矩阵的时候前提是两个图像对应区域必须是同一平面。
当一些点在同一个平面P上,而我们在左右I1,I2两张图片均观测到了。设 N T N^T NT是平面的法向量,d为原点到该平面的距离,则对于该平面上任一三维点 X 1 X_1 X1:
![]()
上式右乘到下式右边:
![]()
其中H成为单应矩阵(homography matrix):
![]()
如果令 x = K X x = KX x=KX,x为像素坐标,则上式为:
K − 1 x 2 = ( R + T N T d ) K − 1 x 1 K^{-1}x_2= (R+\frac{TN^T}{d})K^{-1}x_1 K−1x2=(R+dTNT)K−1x1
则 H = K ( R + T N T d ) K − 1 H=K(R+\frac{TN^T}{d})K^{-1} H=K(R+dTNT)K−1
根据空间平面单位和位置不同而产生不同的H映射,实际运用中更多的是直接使用像素坐标而非物理化后的metric 坐标
从形式上看,这不就是三维空间一个平面上二维点与二维点之间的映射关系吗?比如举一个最简单的例子,二维旋转矩阵就是一个简单的单应矩阵:
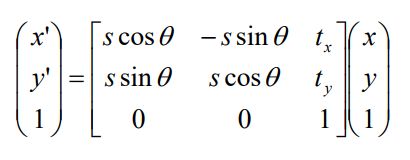
再来一个栗子:
单应矩阵可以将一个二维的正方形做如下变换(r代表旋转矩阵的元素,s表示缩放的标量)
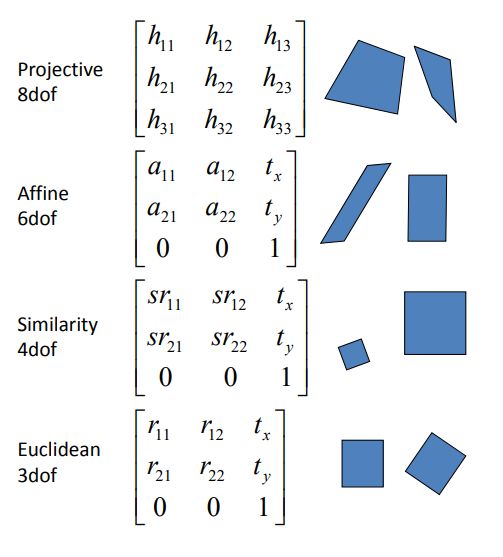
不同视角上观测到的像素坐标关系:
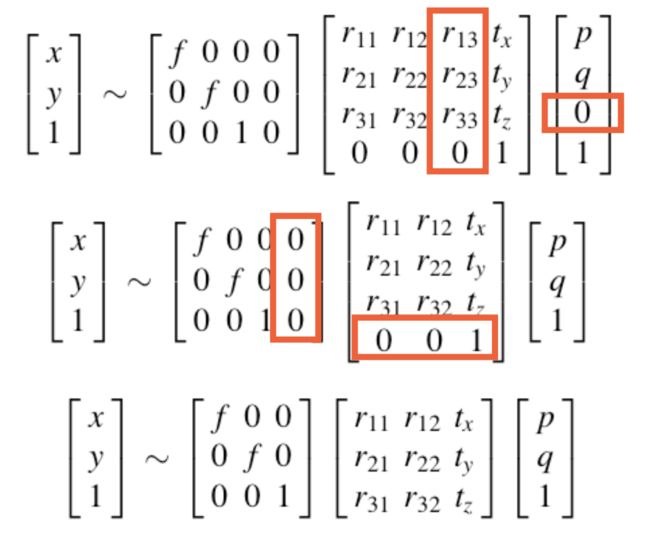
3.3.2数学上的单应性定义
明白了使用场景,我们再来看单应性(homography,在多视图几何中又称为projectivity(射影性),collineation(直射变换,共线性),projective transformation(投影变换))的定义:
定义:
单应性是一个存在于空间 P 2 P^2 P2 内的可逆映射h,h满足:三个点共线当且仅当单应映射后的三个点共线。
或者说:
P 2 − > P 2 P^2->P^2 P2−>P2是单应映射当且仅当存在一个非奇异的8维 3x3矩阵H,对于任何一个 x ∈ P 2 x\in P^2 x∈P2,总能找到对应的点 H x ∈ P 2 Hx\in P^2 Hx∈P2。(这儿的 P 2 P^2 P2是二维空间的齐次表达,可以当成是二维平面空间)
当然单应性不止局限于2x2平面,也可以有n维空间之间的单应映射:
P n − > P n P^n->P^n Pn−>Pn是单应映射当且仅当存在一个非奇异的 ( n + 1 ) 2 − 1 (n+1)^2-1 (n+1)2−1维度的(n+1)方阵H,对于任何一个 x ∈ P n x\in P^n x∈Pn,总能找到对应的点 H x ∈ P n Hx\in P^n Hx∈Pn。
对 x 2 = H x 1 x_2 = Hx_1 x2=Hx1左乘一个 x ^ \widehat x x
x ^ 2 H x 1 = 0 \widehat x_2Hx_1 = \mathbf 0 x 2Hx1=0
这是单应性的另一种形式。
注意这个式子与本征约束式子之间的差别:一个是x叉乘,一个是x转置。化简后本式实际上是一个线性方程组(0是一个3维向量),本征矩阵约束是一个线性方程(0是一个标量),这导致了H约束个数的翻倍:只用四个点对即可求解
**单应性约束与极线约束:**极线约束只是点与对应一条极线的关系,而单应性矩阵约束更强(从单应性矩阵可逆而本征矩阵缺秩也可以看出),是点到点的一一对应。
所以对于物理空间上的同平面
这之后计算H的方法和式(2-1)的处理方式相似,都是根据:
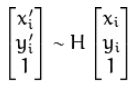
可以用直接线性法(DLT,Direct Linear Transformation)求解线性方程(参见附录1)
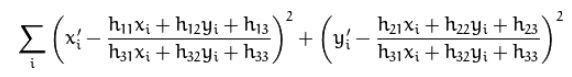
从H组成可以看出H取决于R,T和平面自身的参数。
算出H后,再根据 H = R + 1 d T N T H = R+\frac{1}{d}TN^T H=R+d1TNT 可以求得各项其他参数: 旋转R,法向量N和T/d(注意的是T/d而非两幅图对应pose的平移T),即当d很远时,即离平面很远的情况下,T可能不那么准确,因此全景拼接(d一般较大)时只做纯旋转,效果可能会更好。
此外,实际计算单应性时,由于H对噪声敏感,需要将所有点进行归一化处理成平均值为0,方差为固定(如sqrt(2)),随后根据像素点与像素点的对应关系求出H。
3.3.3单应性矩阵的特殊情况
当T=0,则H=R,即有 X 2 = R X 1 X_2 = RX_1 X2=RX1。此时等价与d为无穷远;或者说,无法计算d,因为d为任何值都可以。
由于实际运用中更多的是直接使用像素坐标而非物理化后的metric 坐标,所以单应矩阵往往为H=KRK’
3.4 基础矩阵(fundamental matrix)
当不知道内参数矩阵时,只有像素坐标,对极约束为:
p 2 T K − 1 T × R K − 1 p 1 = 0 p_2^TK^{-1}T\times RK^{-1}p_1 = 0 p2TK−1T×RK−1p1=0
K − 1 T × R K − 1 K^{-1}T\times RK^{-1} K−1T×RK−1成为基础矩阵F。由于K不影响秩因此矩阵是基础矩阵的充要条件是它的秩为2。可以看出基础矩阵的给与的约束不强。
在SFM,SLAM中我们一般认为相机已经标定好,因此可以直接将基础矩阵求解转化为本征矩阵求解。
3. 单应矩阵和基础矩阵的联系与区别
3.1 联系
本质上,单应性是一种特殊的基础矩阵:
右极线 l r = F x r l_r = Fx_r lr=Fxr
而由于两点叉乘即是过两点的直线参数:
l r = e r × x r = e r × H x l l_r = e_r \times x_r = e_r \times Hx_l lr=er×xr=er×Hxl
所以令:
F = e r × H F = e_r \times H F=er×H
附:E与H的关系
将 E = T ^ R , H = R + T u E = \hat TR,H = R+Tu E=T^R,H=R+Tu相互代入:
E = T ^ H , H T E + E T H = 0 E = \hat T H,H^TE+E^TH = 0 E=T^H,HTE+ETH=0
当有位移(translation)的时候,才有对极几何关系;当位移为0时,就是单应关系。
表达式结构不同,单应矩阵中一个点对可以产生两组约束,而对于基础矩阵一个点对只能产生一组约束。但都可以表示二维像素坐标之间的映射关系
3.2 不同
-
几何角度上:一个是点与线的关系(基础矩阵表达的极限约束),一个是点与点之间的约束(单应性)
-
代数角度:基础矩阵是秩为2的奇异矩阵,单应矩阵秩为3的非奇异矩阵
-
当用于求解F时的点(八点法或者五点法)都在同一个平面上或者相机发生纯粹旋转时,基础矩阵自由度退化,这时如果用求解E的方式来求解R,T,那么E将极大受噪音影响。此时求解单应矩阵来求解R,T往往更合适。所以初始化时我们一般同时用求解E,H两种方法来分别得到R,T,然后选择重投影误差更小的那种方法
4.结构信息重建(地图点三维信息)
求出R,T后,对于某点对,其 关系如下:
![]()
其中:
γ = ∣ ∣ E ∣ ∣ = ∣ ∣ T ^ R ∣ ∣ = ∣ ∣ T ^ ∣ ∣ = ∣ ∣ T ∣ ∣ = σ 2 , σ 是 特 征 矩 阵 E 的 S V D 分 解 的 特 征 值 \gamma = ||E||=||\hat T R|| =||\hat T|| = ||T|| = \sigma^2,\sigma是特征矩阵E的SVD分解的特征值 γ=∣∣E∣∣=∣∣T^R∣∣=∣∣T^∣∣=∣∣T∣∣=σ2,σ是特征矩阵E的SVD分解的特征值 是尺度因子。因为(2-2)中将尺度因子放入E中了。归一化的E行列式为1,即 Σ = { 1 , 1 , 0 } 2 \Sigma = \{1,1,0\}^2 Σ={1,1,0}2
但 λ i j 无 法 求 得 \lambda_i^j无法求得 λij无法求得。为此对左右乘以 λ 2 j ^ : \hat {\lambda_2^j}: λ2j^:
![]()
上式可以写作:
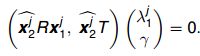
对与所有点对 ( x 1 j , x 2 j ) , j = 1 , 2 , 3 , . . . (x_1^j,x_2^j),j = 1,2,3,... (x1j,x2j),j=1,2,3,...,则有:
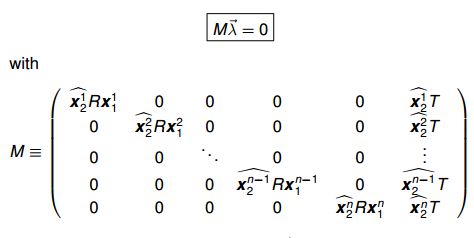
![]()
λ ⃗ \vec \lambda λ即是 M T M M^TM MTM的特征向量;
可求出所有点的实际三维点 λ j ( x , y , 1 ) T \lambda^j(x,y,1)^T λj(x,y,1)T信息和尺度因子 γ \gamma γ。
附录
- 直接线性法:multi-view geometry
- homograph:
homograph1
homograph2 - 单应矩阵与基础矩阵的区别