校内互测 C. 向量 (乱搞+随机+数论)
C. 向量
时间限制:1s 内存限制:128MB
题目描述
一个d 维向量是一个d 元组,或者你也可以把它看成一个数组。比如(2,3,3)就是一个三维向量。特别的,一维向量也是一个一元组,但它并不是一个数。向量的加法就是将向量的每一维对应相加,比如 A=(2,3,3),B=(6,6,6),那么A+B=(8,9,9)。向量的点/内积就是将向量的每一维对应相乘之后再求和,即
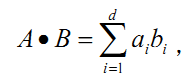
,在上面的例子中就有A·B=156。给出n 个d维向量, 请寻找两个向量使得它们的点积是k的倍数。
输入格式
第一行三个正整数n,d,k。
接下来n 行,每行d 个非负整数描述向量xi。
输出格式
如果有解,输出一行两个正整数p,q(p
3 5 2
1 0 1 0 1
1 1 0 1 0
0 1 0 1 1
输出样例
2 3
数据范围
题解:乱搞+随机。
我们如果枚举向量对肯定会TLE。所以我们考虑利用向量的分配律。
当k=2的时候,具体的,我们枚举向量xi,判断xi*(sigma(j=1..i-1)xj)%k是否等于(i-1)%k,如果不相等,说明x1...xj-1之间存在向量与xi的点积为0 (在模2意义下)。为什么呢,向量是满足分配率的,所以上式的结果相当于是将xi于他之前的向量分别相乘再加和,如果不存在点积为0的,那么答案一定是(i-1)%2。但是这样还有可能不对,因为当存在两个或偶数个点积为0,xi*(sigma(j=1..i-1)xj)%k==(i-1)%k,但是实际上是存在答案的。
但是这样的概率非常小,每次都有1/2的概率,(1/2)^n已经接近0了,我们再random_shuffle3到4次,计算一下,应该就可以解决了。
当k=3的时候,取模后不等于0的情况就有1,2两种,这要怎么办呢?我们考虑给向量平方,因为1,2平方%3都等于1.
我们还是要利用前缀和和向量的分配律。
我们现在要求sigma(j=1..i-1) (xi*xj)^2 先看(xi*xj)^2这一部分,
向量的点/内积就是将向量的每一维对应相乘之后再求和,而点积的平方就是将d维向量变成一个d^2维的向量矩阵,然后让矩阵中的每个位置对应相乘再相加。
(a1*b1+a2*b2)^2=a1^2*b1^2+2*a1*a2*b1*b2+a2^2*b2^2
= { a1^2 ,a1*a2 * {b1^2, b1*b2
a1*a2,a2^2 } b1*b2,b2^2 }
有这个性质之后,我们发现sigma(j=1..i-1) (xi*xj)^2 就相当于1..i-1个矩阵分别与xi形成的矩阵相乘,因为是对应位置相乘再相加,所以满足分配律,将x1..xi-1个向量形成的矩阵对应位置相加得到一个新矩阵,再与xi形成的矩阵相乘得到答案,看答案是否=(i-1)%3,如果不等于就可以扫一遍x1..xi-1统计答案即可。
#include
#include
#include
#include
#include
#include
#define N 100003
using namespace std;
int n,m,k;
int a[103][103],b[103],now[103][103];
int c[N],num[N][103];
void add(int x,int ans[])
{
for (int i=1;i<=m;i++)
ans[i]=(ans[i]+num[x][i])%k;
}
void add1()
{
for (int i=1;i<=m;i++)
for (int j=1;j<=m;j++)
a[i][j]=(a[i][j]+now[i][j])%k;
}
void change(int x)
{
for (int i=1;i<=m;i++)
for(int j=1;j<=m;j++)
now[i][j]=num[x][i]*num[x][j]%k;
}
void pd(int x)
{
for (int i=1;it1) swap(t,t1);
printf("%d %d\n",t,t1);
exit(0);
}
}
}
int main()
{
freopen("vector.in","r",stdin);
freopen("vector.out","w",stdout);
scanf("%d%d%d",&n,&m,&k);
for (int i=1;i<=n;i++)
for (int j=1;j<=m;j++) scanf("%d",&num[i][j]);
if (n<=1000)
{
for (int i=1;i<=n-1;i++)
for (int j=i+1;j<=n;j++)
{
int tot=0;
for (int t=1;t<=m;t++)
tot=(tot+num[i][t]%k*num[j][t]%k)%k;
if (tot%k==0) {
printf("%d %d\n",i,j);
return 0;
}
}
printf("-1 -1\n");
return 0;
}
if (k==2)
{
for (int t=1;t<=4;t++)
{
for (int i=1;i<=n;i++) c[i]=i;
random_shuffle(c+1,c+n+1);
memset(b,0,sizeof(b));
add(c[1],b);
for (int i=2;i<=n;i++)
{
int tot=0;
for (int j=1;j<=m;j++)
tot=(tot+num[c[i]][j]*b[j])%k;
if (tot!=(i-1)%k) pd(i);
add(c[i],b);
}
}
printf("-1 -1\n");
return 0;
}
for (int i=1;i<=n;i++) c[i]=i;
// random_shuffle(c+1,c+n+1);
change(c[1]); add1();
for (int i=2;i<=n;i++)
{
int tot=0;
change(c[i]);
for (int j=1;j<=m;j++)
for (int k1=1;k1<=m;k1++)
tot=(tot+now[j][k1]*a[j][k1])%k;
if (tot!=(i-1)%k) pd(i);
add1();
}
printf("-1 -1\n");
return 0;
} 
