Play a game (博弈论)
Play a game
ailyanlu is very happy today! and he is playing a chessboard game with 8600.
The size of the chessboard is n*n. A stone is placed in a corner square. They play alternatively with 8600 having the first move. Each time, player is allowed to move the stone to an unvisited neighbor square horizontally or vertically. The one who can't make a move will lose the game. If both play perfectly, who will win the game?
Input The input is a sequence of positive integers each in a separate line.
The integers are between 1 and 10000, inclusive,(means 1 <= n <= 10000) indicating the size of the chessboard. The end of the input is indicated by a zero. Output Output the winner ("8600" or "ailyanlu") for each input line except the last zero.
No other characters should be inserted in the output. Sample Input
2 0Sample Output
8600
同理,n为奇数时,后手胜。
证明:首先我的证明基于一个事实:1个奇数总能分成1个奇数和1个偶数之和;1个偶数只能分成2个奇数或者2个偶数。
先来看看n=4时的情况:
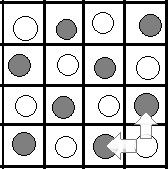
不妨设最右下角的位置为开局时棋子所在的位置。
那么如图1,灰色的部分为先手可以走的格子,白色的部分为后手可以走的格子。
(PS:就像国际象棋中的黑格象只会走到黑格中,白格象只会走到白格中。
那么本题为什么是这样?是因为规则规定每次只能向外走一步而且只能上下左右走。
所以一旦起点定下来,第一步是先手走,走到灰色格子,以后奇数的步数都是先手。
所以离起点曼哈顿距离是奇数的都是先手走的。)
图1
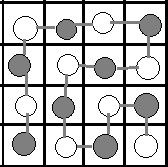
我们来看一个走的实例:
图2
图2是一个先手赢的结局,通过这个例子可以发现如果这根时间线最后的终点是灰色就是先手胜(废话!先手下完,然后后手不能下了游戏就结束了,这不就是题目的要求么!)。
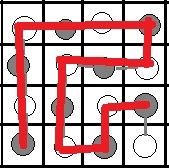
那么由于一开始走的时候就是先手,所以时间线的起点是灰色(如图3)。
图3(红色为时间线)( 名字好像有点中二啊……)
如果要出现N(后手输)的结果,时间线最后也要是以灰色结尾。
这说明什么?
要知道这是一个灰色白色交替的时间线!
所以这就意味着时间线的长度是奇数(以第一个灰色为起点,连接了多少个点长度就是多少,图2的长度为15)!
由于起点一定是灰色,所以当n*n-1(n为偶数时)为奇数的时候,事实上是最长的那个时间线为奇数——如果按这个时间线走一定是先手胜。
但是这样还是没有说为什么一定会赢啊!
于是我们的前提可以派上用场了,1个奇数总能分成1个奇数和1个偶数之和。
对方才不会那么蠢,走我们安排的最长路线,但是“1个奇数总能分成1个奇数和1个偶数之和”也就是说,把这条路线长度分割,一定能找到比这条路线短的另一个奇数路线,因为我们是先手,所以我们控制走分出来的奇数的路,而不是引向偶数的路。
由于n是偶数,我们又是先手,每次都是先手面临时间线是奇数的情况,所以一定能赢。
而如果n是奇数,那么最长路是偶数,我们走后就变成以白格为首的奇数长度了,然后每次都是后手面临时间线是奇数的情况,所以先手就输了。
原证明博客网址code:
#include
#include
#include
using namespace std;
int main(){
int n;
while(~scanf("%d",&n)&&n){
if(n&1)
printf("ailyanlu\n");
else
printf("8600\n");
}
return 0;
}