斐波拉契快速求法:矩阵快速幂
斐波拉契数:f0=0,f1=1,……..fn=f[n-1]+f[n-2]
用矩阵表示: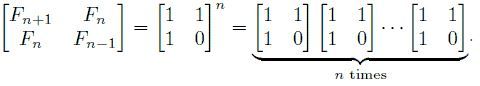
2*2的矩阵用结构体表示:
struct node{
int a,b;
int c,d;
};2*2矩阵乘法:
node mult(node x,node y){
return {x.a*y.a+x.b*y.c,x.a*y.b+x.b*y.d,x.c*y.a+x.d*y.c,x.c*y.b+x.d*y.d};
}矩阵快速幂和数的快速幂一样,不过要注意矩阵的0次幂为E(单位矩阵,任何矩阵与E相乘保持不变)
node fast(node x,int n){
if(n==0)return {1,0,0,1};//单位矩阵,相当于数1
if(n%2)return mult(x,fast(x,n-1));
node tmp=fast(x,n/2);
return mult(tmp,tmp);
}因此 f[ n ] = fast( {1,1,1,0} , n ).b