卡尔曼滤波

首先补充统计里面的知识点：
1.协方差统计里最基本的概念均值，标准差，方差，均值就是样本的平均，而标准差就是样本中的每个数据到均值的距离，方差就是标准差的平方：例如有两个样本空间：{1，5，9}和{4，5，6}显然这两个样本空间的均值都是5，但实际可以看出这两个数据还是有很大差距的，所以我们又引入标准差和方差的概念。标准差是方差的开根号，上面两个数据的标注差一个是4，后面一个是1，很显然后面一个数据的标准差更小。标准差描述的是一个数据的离散程度，标准差越小，表明其数据越集中。
a.均值公式(E（x）)：（x为样本空间数据）

b.方差公式(D(x))：（M为平均值，x为样本空间数据）

c.标准差公式（σ）：（样本空间中）
=s=sqrt(((x1-x)^2 +(x2-x)^2 +…(xn-x)^2)/n-1)。也就是方差开根号，由于是样本空间，所以里面是除以（n-1）

以上就是统计里面描述数据的三个常用方法。但是这些数据都是解决一维的数据。当我们要研究二维问题，也可以说是二维关系问题时，以上三个用法对于独立变量有意义，但对于相互影响的数据则需要用到协方差来解决。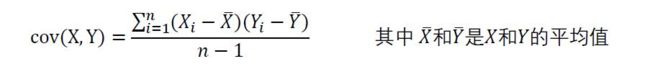
上面就是协方差的公式：

    正相关：假设有两个变量x和y，若x越大y越大；x越小y越小则x和y为正相关。

    负相关：假设有两个变量x和y，若x越大y越小；x越小y越大则x和y为负相关。

    不相关：假设有两个变量x和y，若x和y变化无关联则x和y为负相关。

下面是相关系数：用X、Y的协方差除以X的标准差和Y的标准差。

更准确地说是线性相关性，是一个衡量线性独立的无量纲数，其取值在[0,+1]之间。相关性η = 1时称为“完全线性相关”，此时将Yi对Xi作Y-X 散点图，将得到一组精确排列在直线上的点；相关性数值介于0到1之间时，其越接近1表明线性相关性越好，作散点图得到的点的排布越接近一条直线。

相关性为0（因而协方差也为0）的两个随机变量又被称为是不相关的，或者更准确地说叫作“线性无关”、“线性不相关”，这仅仅表明X 与Y 两随机变量之间没有线性相关性，并非表示它们之间一定没有任何内在的（非线性）函数关系，和前面所说的“X、Y二者并不一定是统计独立的”说法一致。

协方差可以用来解决很多生活中的二维问题：例如买房的人数与房价的关系。出生人口与房价的关系等。现实
协方差也只能处理二维问题，那维数多了自然就需要计算多个协方差，比如n维的数据集就需要计算 n! / ((n-2)!*2) 个协方差，那自然而然的我们会想到使用矩阵来组织这些数据。给出协方差矩阵的定义：

这个定义还是很容易理解的，我们可以举一个简单的三维的例子，假设数据集有三个维度，则协方差矩阵为

可见，协方差矩阵是一个对称的矩阵，而且对角线是各个维度上的方差。

2.正态分布：正态分布（Normal distribution)是一种概率分布。正态分布是具有两个参数μ和σ^{2的连续型随机变量的分布，第一参数μ是遵从正态分布的随机变量的均值，第二个参数σ}2是此随机变量的方差，所以正态分布记作N(μ，σ^2 )。遵从正态分布的随机变量的概率规律为取 μ邻近的值的概率大 ，而取离μ越远的值的概率越小；σ越小，分布越集中在μ附近，σ越大，分布越分散。

正态分布的密度函数的特点是：关于μ对称，在μ处达到最大值，在正（负）无穷远处取值为0，在μ±σ处有拐点。它的形状是中间高两边低 ，图像是一条位于x 轴上方的钟形曲线。当μ＝0，σ^2 ＝1时，称为标准正态分布，记为N（0，1）。


概率分布公式为：

下面开始进入正题：
卡尔曼滤波白话解释（转载）：
假设你有两个传感器，测的是同一个信号。可是它们每次的读数都不太一样，怎么办？
取平均。
再假设你知道其中贵的那个传感器应该准一些，便宜的那个应该差一些。那有比取平均更好的办法吗？
加权平均。
怎么加权？假设两个传感器的误差都符合正态分布，假设你知道这两个正态分布的方差，用这两个方差值，（此处省略若干数学公式），你可以得到一个“最优”的权重。接下来，重点来了：假设你只有一个传感器，但是你还有一个数学模型。模型可以帮你算出一个值，但也不是那么准。怎么办？
把模型算出来的值，和传感器测出的值，（就像两个传感器那样），取加权平均。
OK，最后一点说明：你的模型其实只是一个步长的，也就是说，知道x(k)，我可以求x(k+1)。
问题是x(k)是多少呢？答案：x(k)就是你上一步卡尔曼滤波得到的、所谓加权平均之后的那个对x在k时刻的最佳估计值。
于是迭代也有了。这就是卡尔曼滤波。
参考：http://blog.csdn.net/karen99/article/details/7771743
比如我们的观查值是Z，估计值是X， 那么新的估计值就应该是 Xnew = X + K ( Z-X），从这个公式可以看到，如果X估计小了，那么新的估计值会加上一个量K ( Z-X）, 如果估计值大了,大过Z了，那么新的估计值就会减去一个量K ( Z-X），这就保证新的估计值一定比现在的准确，一次一次递归下去就会越来越准却了，当然这里面很有作用的也是这个K，也就是我们前面说的权值，书上都把他叫卡尔曼增益。。。(Xnew = X + K ( Z-X） = X ×（1-K) + KZ ，也就是说估计值X的权值是1-k，而观察值Z的权值是k，究竟k 取多大，全看估计值和观察值以前的表现，也就是他们的方差情况了）

参考：https://blog.csdn.net/lovebaby859450415/article/details/79082459
卡尔曼滤波模型理论建立在线性代数和隐含马尔可夫模型。其基本动态系统可以用一个马尔可夫链表示，该马尔可夫链建立在一个被高斯噪声(即正态分布的噪声)干扰的线性算子上的。系统的状态可以用一个元素为实数的向量表示。 随着离散时间的每一个增加,这个线性算子就会作用在当前状态上，产生一个新的状态,并也会带入一些噪声,同时系统的一些已知的控制器的控制信息也会被加入。同时，另一个受噪声干扰的线性算子产生出这些隐含状态的可见输出。

卡尔曼滤波器的递归过程：

1. 估计时刻kk 的状态：
   X(k)=A∗X(k−1)+B∗u(k)
   X(k)=A∗X(k−1)+B∗u(k)

u(k)u(k) ，是系统输入，ll维向量，表示kk时刻的输入;
X(k)X(k)，nn维向量，表示kk时刻观测状态的均值;
AA，n∗nn∗n矩阵，表示状态从k−1k−1到kk在没有输入影响时转移方式;
BB，n∗nn∗n矩阵，表示u(k)u(k)如何影响x(k)x(k).
2) 计算误差相关矩阵PP, 度量估计值的精确程度：
P(k)=A∗P(k−1)∗AT+Q
P(k)=A∗P(k−1)∗AT+Q

PkPk，n∗nn∗n方差矩阵，表示kk时刻被观测的nn个状态的方差。
Q=E(W2j)Q=E(Wj2) 是系统噪声的协方差阵，即系统框图中的WjWj的协方差阵, QQ 应该是不断变化的，为了简化，当作一个常数矩阵。
3) 计算卡尔曼增益：
K(k)=P(k)∗HT∗(H∗P(k)∗HT+R)−1
K(k)=P(k)∗HT∗(H∗P(k)∗HT+R)−1

这里R=E(V2j)R=E(Vj2), 是测量噪声的协方差(阵), 即系统框图中的 VjVj 的协方差, 为了简化，也当作一个常数矩阵;
HH，m∗nm∗n矩阵，表示状态x(k)x(k)如何被转换为观测z(k)z(k)。
由于我们的系统一般是单输入单输出，所以RR是一个1×11×1的矩阵，即一个常数，上面的公式可以简化为:
K=P(k)∗HT(H∗P(k)∗HT+R)
K=P(k)∗HT(H∗P(k)∗HT+R)
4) 状态变量反馈的误差量：
e=Z(k)–H∗X(k)
e=Z(k)–H∗X(k)

这里的 Z(k)Z(k) 是带噪声的测量量
5) 更新误差相关矩阵PP
P(k)=P(k)–K∗H∗P(k)
P(k)=P(k)–K∗H∗P(k)
6) 更新状态变量：
X(k)=X(k)+K∗e=X(k)+K∗(Z(k)–H∗X(k))
X(k)=X(k)+K∗e=X(k)+K∗(Z(k)–H∗X(k))
7) 最后的输出：
Y(k)=H∗X(k)
Y(k)=H∗X(k)
5. Kalman Filter 测试
6. 总结
REFERENCE
1 http://bbs.21ic.com/icview-292853-1-1.html
2 http://blog.csdn.net/xiahouzuoxin/article/details/39582483
3 http://blog.csdn.net/yangtrees/article/details/8075911
4 http://www.cnblogs.com/ycwang16/p/5999034.html
5 http://blog.csdn.net/heyijia0327/article/details/17487467
6 http://blog.csdn.net/heyijia0327/article/details/17667341
7 https://en.wikipedia.org/wiki/Kalman_filter
Paper:http://www.cl.cam.ac.uk/~rmf25/papers/Understanding the Basis of the Kalman Filter.pdf