卡尔曼滤波_2(图解)
原文链接
卡尔曼滤波器如何描述问题
要估计的状态如下表示:
不知道实际的位置和速度,所有的 (p,v) 组合都有可能,但是有一些组合比其他组合可能性更大:
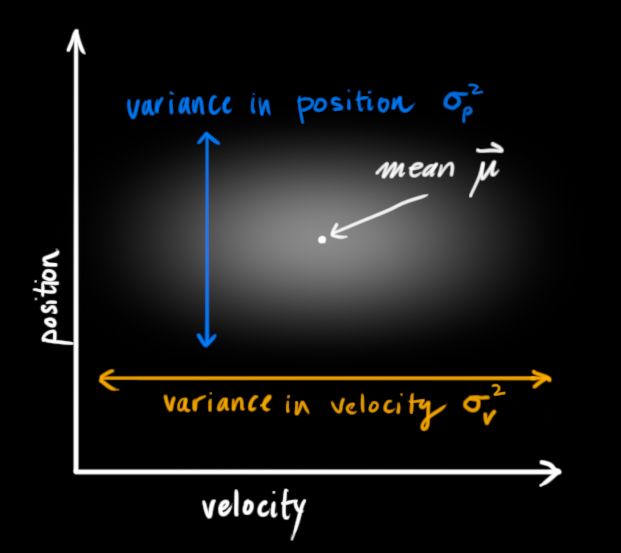
卡尔曼滤波器假设所有的变量(我们的栗子中,位置和速度)都是随机的,而且是高斯分布的。每个变量都有一个均值![]() ,表示随机分布的中心点(即最可能的位置),以及方差
,表示随机分布的中心点(即最可能的位置),以及方差![]() ,表示不确定性。
,表示不确定性。
在上图中,位置和速度是不相关的(uncorrelated)。不相关的意思是说,一个变量的状态无法推测出另一个变量的状态。
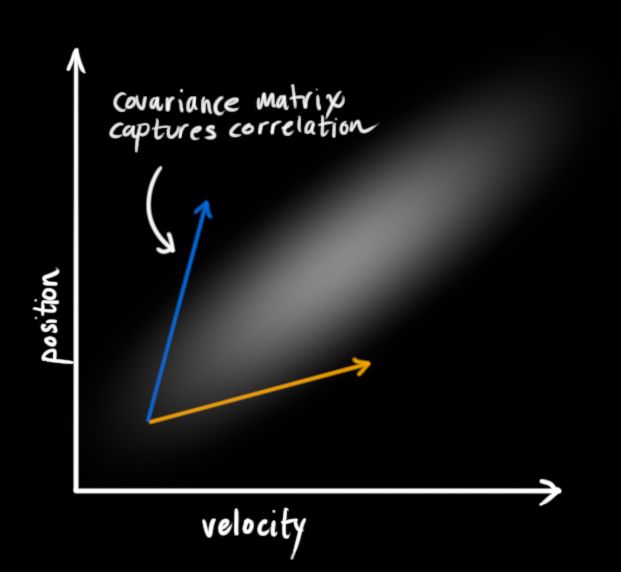
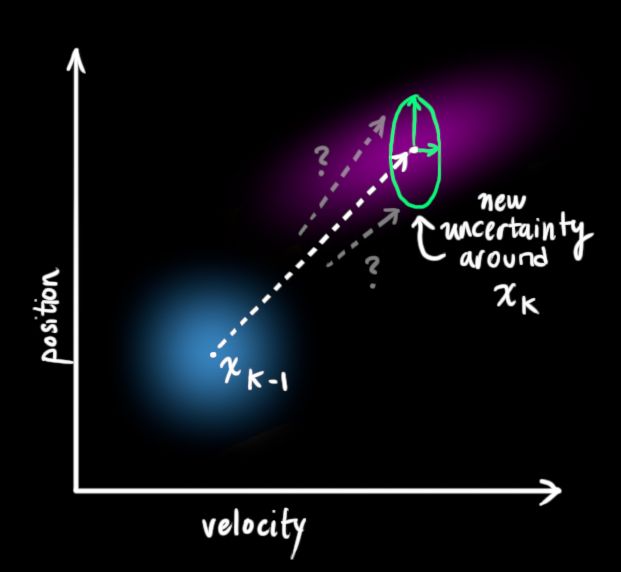
下面这个栗子表明,位置和速度是相关的(correlated)。观测到怎样的位置,取决于观测到怎样的速度。
这种情况可以出现在这样的例子中:我们要从旧的位置估计新的位置。如果速度大,那么新位置也会离旧位置远;相反如果速度小,新位置会靠近旧位置。
这种关系非常重要,因为它给予我们更多的信息:对一个变量的测量,可以告诉我们其他变量的信息。这就是卡尔曼滤波器的目标所在:我们希望从不确定的测量中,尽量多的获得信息。
这个相关性用一种叫做协方差矩阵(covariance matrix)来描述。简而言之,矩阵中第i行第j列的元素,表示的是第i位置的变量和第j位置变量的相关程度。(你可以推测,这样的矩阵是对称矩阵,意味着交换i和j的位置没有影响。)协方差矩阵习惯上简写成![]() ,第ij个元素写成
,第ij个元素写成![]() .
.
用矩阵描述问题
我们用高斯块(Gaussian blob)来描述状态的所有信息,所以在时刻k,我们需要2种信息:最佳估计![]() (均值,也叫
(均值,也叫![]() ),还有它的协方差矩阵
),还有它的协方差矩阵![]()
这里仅仅使用了位置和速度两个变量,但要记住的是,卡尔曼滤波器可以对任意数量的变量进行描述,只要你愿意。
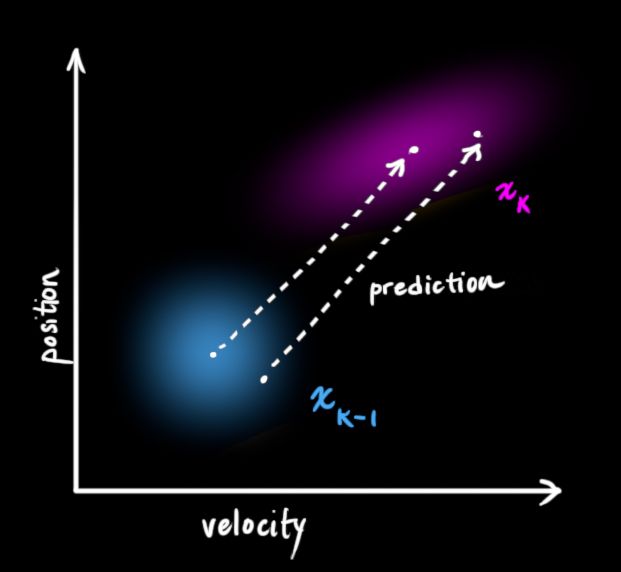
当前时刻(k-1)和下一时刻(k)的状态,我们需要描述出来。要记住,我们并不知道状态的真实值,而且预测函数也不在意这一点。预测函数对所有可能的值,都进行处理,并给出一个新的分布。
用![]() 来表示预测这一步。
来表示预测这一步。
它把上一次估计的每一个点都映射到新的估计位置。如果上一次估计是正确的,这就是系统的移动方向。
用数学公式对上面这个过程进行描述,利用基本运动学公式:
![]()
![]()
也可以写成
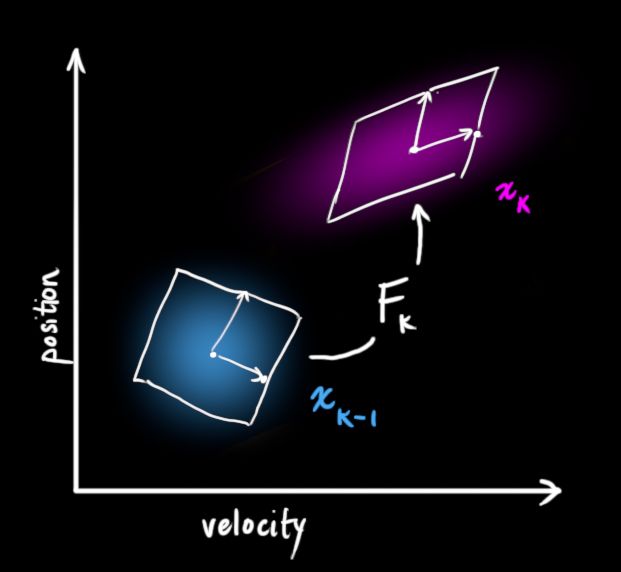
现有我们有一个预测矩阵可以给出下一个状态,但是我们还是不知道怎么更新协方差矩阵。
这就需要另一个公式了。如果我们对分布中的每一个点乘上一个矩阵A,它对应的协方差会有什么变化呢?
结合上面两个式子,可以得到下面的表达
外部已知影响
我们的描述还不够,还有一些和状态本身无关,外部的世界也会对系统产生影响。
例如,如果状态描述的是火车的动作,列车长可能会给火车提速。类似的,在机器人栗子中,导航系统也许会发出指令来控制轮子启动还是停止。如果我们知道这个外部世界对系统带来了哪些影响的话,可以用一个向量来表示这些影响,![]() ,把它加到我们的预测里来修正预测。
,把它加到我们的预测里来修正预测。
……(公式描述参见原文)
外部未知影响
如果状态仅仅依靠它自身属性发展的话,甚至包括外部已知的影响,一切都将准确预测。但是如果还存在位置的外部影响呢?
例如,我们跟踪无人机,无人机可能会受风力的影响。我们跟踪地面机器人,它会受到地面不平的影响。这些影响我们无法记录,如果发生了其中一项,我们的预测就失败了。所以,需要添加不确定项。
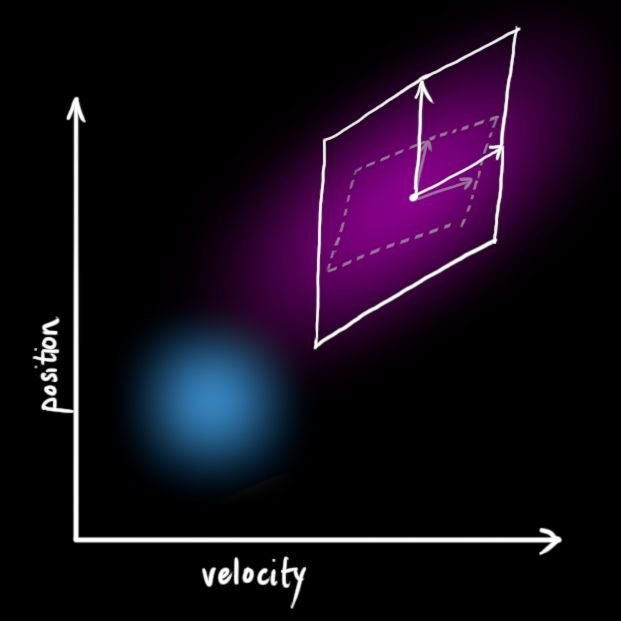
上一次估计的每一个状态值映射到一个状态区域内。由于高斯块非常形象,所以我们说,![]() 中的每一个点被映射到一个协方差
中的每一个点被映射到一个协方差![]() 描述的高斯块中。换个说法,我们用协方差
描述的高斯块中。换个说法,我们用协方差![]() 描述未知的外部影响,并认为是噪声。
描述未知的外部影响,并认为是噪声。
这就产生了一个新的高斯块,和之前的相比,均值相同,协方差不同。
通过添加![]() 我们得到了预测步骤的完整表达:
我们得到了预测步骤的完整表达:
换句话说,最佳的估计值,是上一次最佳估计值,加上已知外部影响的修正。
而最佳不确定性的预测,是从上一次不确定中,增加了环境中额外的不确定性。
到目前为止,都挺简单的,我们对系统有一个大概的估计。如果我们从传感器获得一些数据呢?
用测量数据重新定义估计
我们也许有一些传感器,可以获得关于系统状态的信息。每个传感器测量什么暂时来说,并不重要,也许一个测量位置,另一个测量速度。每个传感器间接地告诉我们状态的信息。换句话说,这些传感器作用在状态上,产生一系列读取结果。
忽略测量数值的单位和尺度,也许会和我们要预测的状态量有所不同。我们用![]() 来描述传感器作用。
来描述传感器作用。
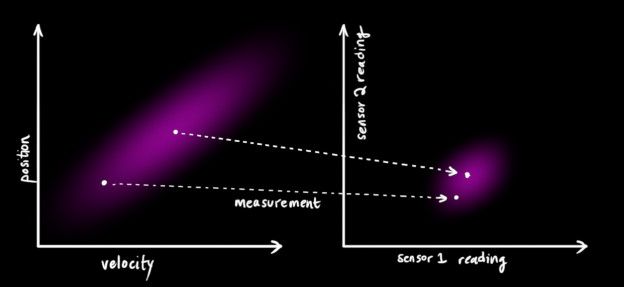
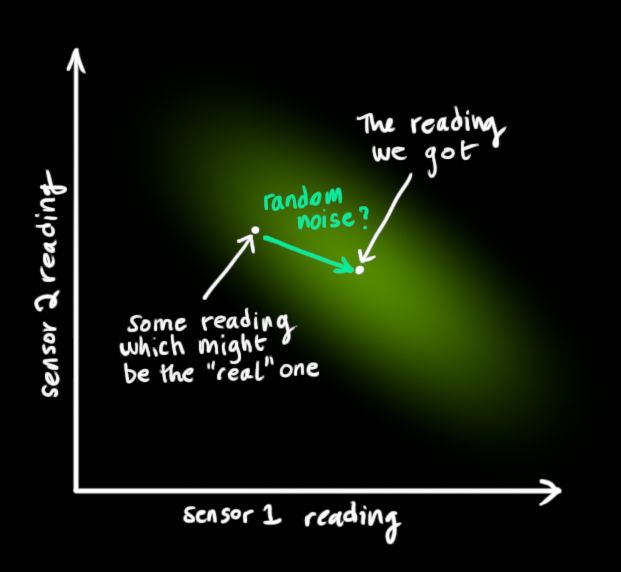
传感器读取的数值的分布可以用下面这种方式表示:
卡尔曼滤波器的伟大之处之一在于,它能处理传感器噪声。换句话说,传感器是不可靠的,上一次估计中的每一个取值,都会映射到一个范围里面。
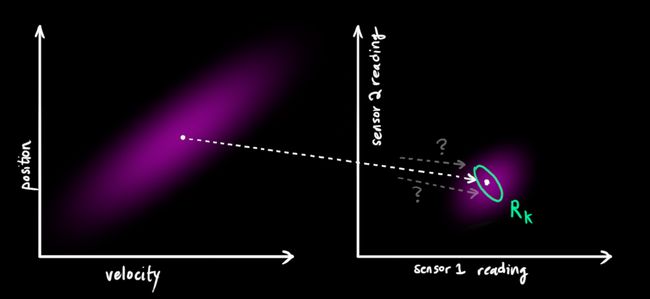
从观测量中也许可以猜测系统所处的状态。但是由于它是不确定的,一些取值比另一些取值更容易产生观测结果。
把这种不确定性的协方差(也叫传感器噪声)记作![]() 。分布的均值就是我们观测到的值,记作
。分布的均值就是我们观测到的值,记作![]() .
.
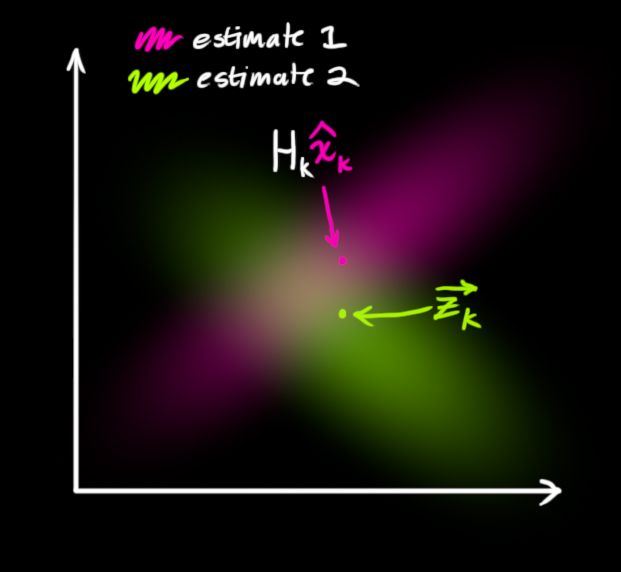
所以,现在有两个高斯块:一个是以根据传输关系得到的预测值为均值的高斯块,另一个是以实际传感器测得的值为均值的高斯块。
我们需要在两者中找到平衡点。哪个是最可能的状态呢?在所有的状态组合可能中,我们有两个概率:(1)传感器的估计值 (2)上一次最佳估计的估计值。
一般来说,如果我们有两个概率分布,想知道两个事件都发生的概率,那把两个概率相乘就好了。所以,把这两个高斯块相乘:
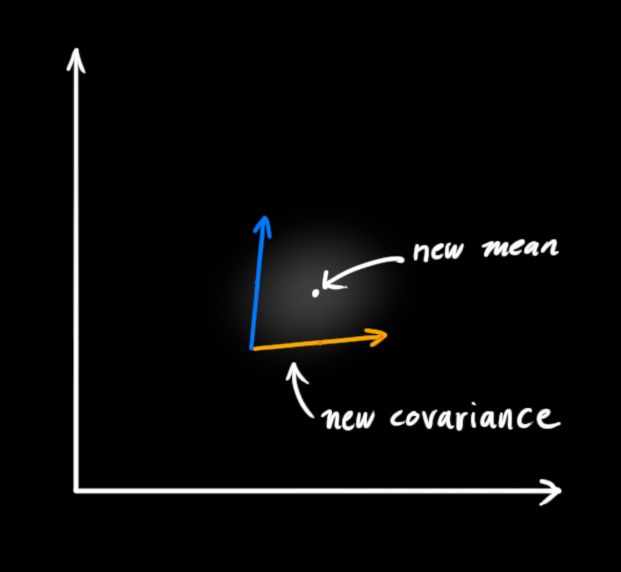
剩下的就是重合部分,这部分两个高斯块的概率取值都比较大,而且这里面的取值比之前的估计取值,都要准确。这个重合部分的均值,就是两部分估计最最有可能的值,这就是最佳估计。这就像是另外一个高斯块:
结果就是,当你把两个高斯块相乘,你可以获得一个新的高斯块,它有自己的均值和协方差。也许你能看出来,这里需要一个公式化的表达。
结合高斯分布
公式太多,参考原文
写成卡尔曼滤波器标准形式
公式太多,参考原文
总结
卡尔曼滤波器可以对线性系统精确描述。对于非线性系统,我们使用EKF。EKF仅仅是对预测和测量的均值进行线性化。
如果我以上的工作还凑活,希望有人可以感受到卡尔曼滤波器的伟大之处,并把这个方法用到之前没有用过的问题中。
******************END******************
我的感受:
- 能够图形化地理解一个算法,才是真正理解了算法的魅力。感谢Bzarg写的这篇博客。
- 高斯块,对于理解高斯分布的均值和协方差,很到位。
- 看这篇博客,简直是一种享受。