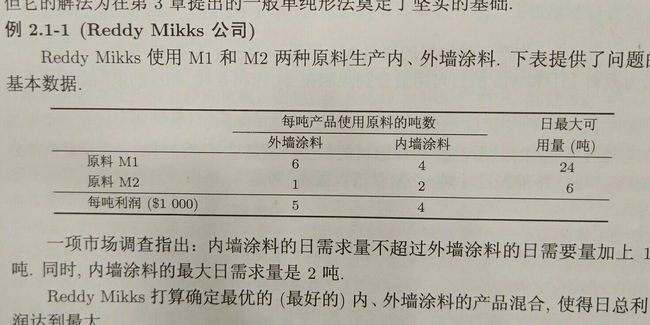
线性规划:单纯形算法

作者 dylanFrank(滔滔)

转载请联系作者 原文链接：http://blog.csdn.net/Dylan_Frank/article/details/77876006

这里简要总结一下线性规划的单纯形算法，做如下几个方面的总结，其余以后再来填坑.

• 几何表示
• 标准型的代数解法
• 其他情形与标准型的互换
• 退化情形

几何表示

先看这样一个问题

我们很容易用下面的数学语言来描述这个问题

max zs.t 6x1+4x2x1+2x2−x1+x2x2xi=5x1+4x2≤24≤6≤1≤2≥0

如果我们用几何来描述这个问题的话则是这样的

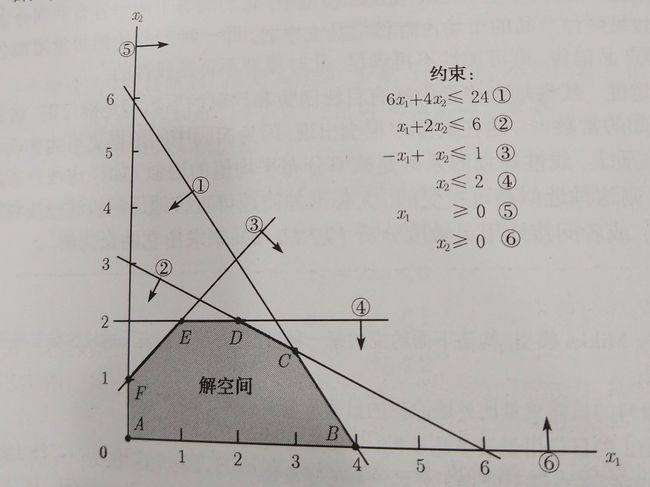
其中阴影部分表示可行域(feasible region)
黑色加粗的线条表示边界
两个边界的交点称为角点(corner-point CP)
在可行域上的角点称谓 角点可行解(CPF)
共享一边的角点称为角点邻接角点(adj CPF)
我们在这里不加证明的指出(以后有空再填坑),线性规划的最优解一定在 CPF ,并且有优性测试 (optimal test),若某一个CPF 的相邻角点的（目标函数）值都不比这个CPF优，则这个CPF 就是最优解.
由此我们不难得到一个简单的算法:

从一个初始CPF开始，沿着比它更优的
adj CPF 前行，若找到一个 CPF 这个CPF的所有 adj CPF不比 它优，则这就是最优解.比如上例中会在C点找到最优解

这就是单纯形算法，不过几何表示毕竟不能让计算机简单执行，因此我们需要将其转化为代数形式。

代数形式

线性规划的标准代数表达，(本文采用《introduction to operation research》清华大学影印版) 的表示.

max zs.t ∑i=1najixixi=∑i=1ncixi≤bj(j=1,2,…,m)≥0,i=1,2,3,…,n

我们后面会发现其他的形式都可以很容易表示为标准形式.

单纯形(simplex) 算法

我们看到，由上面几何版的simplex 算法，我们首先需要一个初始解，为了方便找到初始解，同时也为了能让计算机好进行运算，需要把不等式转化为等式，这里我们引入 松弛变量(slack variable),对每个函数约束我们都引入一个松弛变量(slack variable) xn+j，xn+j≥0 比如上面的例子

6x1+4x2≤24

引入松弛变量(以后简写SV) x3, 满足 x3≥0

6x1+4x2+x3=24

可以发现这个式子和上面的约束是等价的(将 x3≥0 移到一边)

引入SV 的形式成为增广形式，(argument form),第一个例子的增广形式为

max zs.t 6x1+4x2+x3x1+2x2+x4−x1+x2+x5x2+x6xi=5x1+4x2=24=6=1=2≥0

这种形式的解称为增广解，需要说明的是这两种解是一致的，增广解的增广变量恰好是用原式表示的,如最优解中一定有:

x3=24−(6x1+4x2)

基解(basic solution)： 这个对应的是原始形式中的角点解的增广.下面简单说一下，基解的性质:

1. #basic var （基本变量的数目）=函数限制的数目。
2. # non-basic var = #var - #basic var = 线性规划系统的自由度
3. non-basic var =0
4. 如果 基本变量满足非负限制，则基解称为 基本可行解(basic feasible solution BF),我们后面需要关注的就是这个基本可行解BF，这对应的是原始形式中的CPF 的扩充。(非松弛变量为0是初始解)

下面介绍单纯形算法:

1. 初始化，解除限制，引入松弛变量，将目标函数写成 (z−(sumni=1cixi)=0) 记作第0行
2. 最优性测试，选出第0行中系数最小的变量（负的最多），判断系数是否小于0,若是结束输出最优解，否则进入迭代,称选中变量为进基变量(变量不为0，成为基本变量)
3. 进入迭代,进基变量对应的列称为轴列,pivot col,进行最优比率测试，判断，进基变量能最大增加多少. 对于轴列中系数大于0的列，用等式右边值除以系数得到每个等式的比率.,最小的一个作为瓶颈行，称为轴行(pivot row)
4. 用轴行进行高斯肖元，回到第二步.

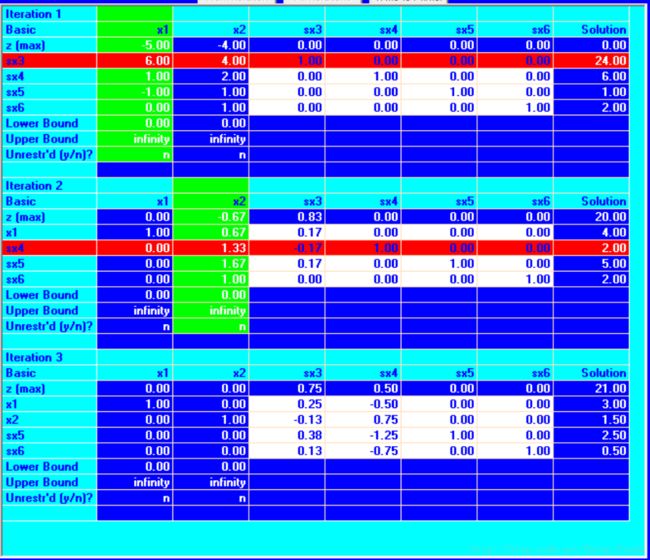
结合具体的例子就好理解了，如上面的第一个例子

使用[taor] 链接：http://pan.baidu.com/s/1hsQUkqo 密码：1ihg《运筹学导论初级篇》 人民邮电出版软件

第一次迭代， x1 的系数最小，且为负，选为pivot col，对其进行最小比率测试，第一行最小，选做pivot row，用它进行高斯肖元，得到第二次迭代的表格. x3 成为非基变量…依次下去得到第3次迭代结果.

需要注意的是第一列标明的变量对应的值为右边的解值.第一行变量中为正的变量取0.

非标准型与标准型的转化

等式限制

处理等式限制 ∑ai∗xi=b ，有两种方法，一种是大M 方法，引入人工变量，一种是将其表示为如下形式

∑ai∗xi∑ai∗xi≤b≥b

大M方法下面再介绍

负的右值限制

∑ai∗xi≤−b,b>0 ,乘一个负号变为 ∑−ai∗xi≥b

大于等于限制

如 0.6x1+0.4x2≥6 , 引入 x3>0 ,转化为等式

0.6x1+0.4x2−x3=6 ,这是等价的

目标函数最小值

目标函数乘-1

xi 边界为负

即如 xi≥−L ,令 x′i=xi−L

无界限制

即 xi∈(−inf,inf) ,
令 xi=x+i−x−i,x+i,x−i>0 ,需要注意的是若有很多变量均是无界限制，可以只取一个变量代替 x−i ，而不必对每个无界变量都引入两个变量.

未完待续…..