相机矩阵(Camera Matrix)

前言

最近翻阅关于从2D视频或者图片中重构3D姿态的文章及其源码，发现都有关于摄像机参数的求解，查找了相关资料，做一下笔记。

国际惯例，来一波参考网址

透视变换、透镜畸变及校正模型、相机校正(Camera Calibration)、Matlab相机校正工具箱、【立体视觉（一）】由基本矩阵、本质矩阵恢复摄像机矩阵——Structure from motion、Multiple View Geometry in Computer Vision(计算机视觉中的多视角几何),附matlab代码 、相机矩阵的分解系列教程、摄像机矩阵详解(中文版)

【注】本文主要提取倒数第二个大牛博客的主要内容，最后一个博客是某位国内大神对这位大牛博客的精解，其它部分为图像知识的补充，主要来源于《OpenGL编程指南》第五章节。博客不在于深究各种细节实现，主要在于对此知识点有所了解，也就是看大牛们的代码的时候至少要知道我们需要求解的东西是什么，都包含什么参数。对理论没兴趣的可以直接看总结，也可看demo展示.

基本知识复习

相机模型

先看看使用相机的主要步骤：

• 移动相机到拍摄位置，镜头对准某个方向(视图变换,view transform)
• 将拍摄对象一到场景中的某个位置(模型变换,model transform)
• 设置相机焦距或调整缩放比例(投影变换,projection transform)
• 对结果图像拉伸或者压缩，变换为需要的图片大小(视口变换,viewpoint transform)

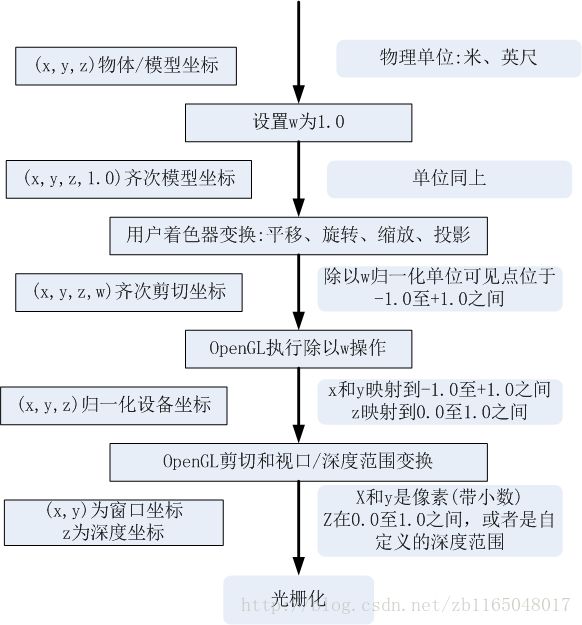
其中前两步可以合并为一个步骤，称为模型-视图变换(model-view transform)，包含多级平移、旋转、缩放。下图摘自OpenGL一书，用于理解对象从一个坐标系统到另一个坐标系统的变换过程

齐次坐标

先看看矩阵乘法在三维坐标变换的缺点：将三维坐标视为一个列向量，那么矩阵*列向量得到的新向量的每一个分量，都是旧的列向量的线性函数，因而三维笛卡尔坐标与矩阵的乘法只能实现三维坐标的缩放和旋转，而无法实现坐标平移。

⎡⎣⎢100001020⎤⎦⎥⎡⎣⎢xyz⎤⎦⎥=⎡⎣⎢x2zy⎤⎦⎥ [ 1 0 0 0 0 2 0 1 0 ] [ x y z ] = [ x 2 z y ]

⎡⎣⎢⎢⎢1000001002000031⎤⎦⎥⎥⎥⎡⎣⎢⎢⎢xyz1⎤⎦⎥⎥⎥=⎡⎣⎢⎢⎢x2zy+31⎤⎦⎥⎥⎥ [ 1 0 0 0 0 0 2 0 0 1 0 3 0 0 0 1 ] [ x y z 1 ] = [ x 2 z y + 3 1 ]

可以发现将三维的笛卡尔坐标添加一个额外坐标，就可以实现坐标平移了，而且保持了三维向量与矩阵乘法具有的缩放和旋转操作。这个就称为齐次坐标。而这种变换也称为仿射变换(affine transformation)，不属于线性变换(线性变换的一个重要规则就是 (0,0,0) ( 0 , 0 , 0 ) 映射以后仍是 (0,0,0) ( 0 , 0 , 0 ) )。

齐次坐标的好处也就显而易见了:

• 进一步完成透视变换,也可戳这里，其实第四个分量就是用于实现透视投影变换的，所有的分量同时处理相同值不会改变它所表达的位置。
• 使用线性变换完成模型的平移

【注意】我们经常将第四个分量记为 w w ，OpenGL会在显示几何体的时候用前三个分量除以第四个分量，从而将齐次坐标变换为笛卡尔坐标。当 w=0.0 w = 0.0 的时候，表示物体位于无限近的位置，透视效果就是无限大的，所以会产生一些无法预知的结果。而且当 w w 是负数的时候，虽然理论可以，但是负数 w w 值可能会给图形管线的某些环节带来麻烦，当与其它的正数 w w 进行计插值计算的时候，导致结果接近或等于0。避免这个问题的方法就是保证第四个分量 w w 为正。

相机矩阵内参和外参的分解

相机矩阵

• 何为几何相机校正(Geometric camera calibration) ?

  也称为相机反切(camera resectioning)，主要用于估计图像或者视频摄像机的透镜和图像传感器的相关参数。使用这些参数可以纠正透镜畸变，度量真实世界中物体的大小，或者相机在一个场景中的定位。因而可以被用于机器视觉，去检测或者度量事物，也可用于机器人中，帮助导航系统和3D重建。

  

• 相机参数都有哪些？估计它们需要的条件？评估所估算的相机参数好坏的标准？

  ①主要包含内参(intrinsics)、外参(extrinsics)、畸变系数(distortion coefficients)

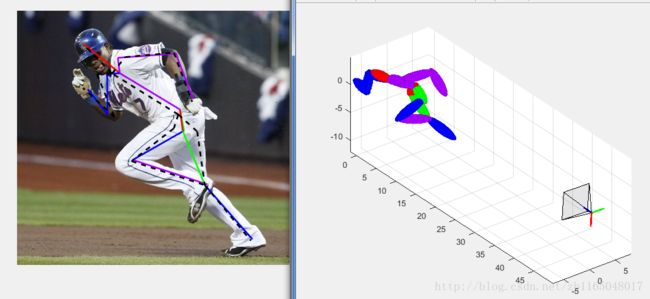
  ②估计参数需要3D世界坐标及其对应的2D图像点。比如在重构3D姿态的时候，需要同时输入图片及图片中对应的人的骨骼2D坐标点。

  ③评估所估计相机参数的方法就是：首先画出相机和校准模式的相对位置；随后计算投影误差；最后计算参数的估算误差。在matlab中有Camera Calibrator来进行相机校准和评估参数精确度。

  

图片代码来源：戳这里1、戳这里2

• 相机矩阵的表示？缺点？

  假设有一个 3∗4 3 ∗ 4 的相机矩阵，可以将齐次3D坐标转换为2D图像坐标。矩阵表示如下
  

  P=[M|−MC] P = [ M | − M C ]
  
  这里的’ | | ’代表的是增广矩阵。其中 M M 代表可逆的 3∗3 3 ∗ 3 矩阵， C C 是列向量，代表世界坐标系中相机位置。

  相机矩阵可以将3D点投影到2D空间，但是有些缺点：

  • 没有提供相机的摆放姿态

  • 没有提供相机的内部几何特征

  • 不能使用镜面光照，因为无法在相机坐标系中得到表面法线向量。

  ​

相机矩阵分解

为了解决上述问题，可以将相机矩阵分解为两个矩阵的乘积：内参矩阵 K K 和外参矩阵 [R|−RC] [ R | − R C ]

P=K[R|−RC] P = K [ R | − R C ]

其中， 3∗3 3 ∗ 3 的上三角阵 K K 描述了相机的内参比如焦距； 3∗3 3 ∗ 3 的旋转矩阵 R R 的列表示相机参考帧的世界坐标轴方向；向量 C C 是世界坐标系中的相机中心。那么向量 t=−RC t = − R C 就给出了相机坐标系中的世界原点位置。我们需要做的就是求解这些参数，当然前提是我们已经知道 P P 了。

相机中心

相机中心的求解比较简单，利用分解前的相机矩阵，由于 P P 的最后一列是由 −MC − M C 得到的，而 M M 在原始的相机矩阵的前 3∗3 3 ∗ 3 部分已经给出了，所以只需要用 −M−1 − M − 1 左乘它即可。

旋转矩阵和内参

首先注意旋转矩阵R是正交的，因为每一列代表的是一个轴(想想三维坐标系的xyz轴是不是垂直的)；而内参矩阵 K K 是一个上三角阵。然后考虑到 QR Q R 分解的用途就是将一个满秩矩阵分解为上三角阵和正交阵的乘积。算法好像不难，matlab的写法如下

function [R Q] = rq(M)
    [Q,R] = qr(flipud(M)')
    R = flipud(R');
    R = fliplr(R);
    Q = Q';   
    Q = flipud(Q);

但是发现 QR Q R 分解的结果不唯一，对 K K 的任何一列以及 R R 的对应行取反(negative)都不会导致相机矩阵结果的改变。

如果满足如下两个条件，可以让 K K 的对角元为正

• 图像的X/Y轴所指方向与相机的X/Y轴方向相同
• 相机处于z轴正方向

所以可以取QR分解中，使得 K K 的对角元为正的解，让 K K 对角元为正的代码如下

# make diagonal of K positive
T = diag(sign(diag(K)));
K = K * T;
R = T * R; # (T is its own inverse)

然而在实际中，照相机和图片的轴经常不统一，所以 K K 的对角元也不应该是正的，如果强制它们为正，将会导致一些不好的副作用，包含：

• 对象位于相机错误的一边
• 旋转矩阵行列式为 −1 − 1 而不是 1 1
• 不正确的镜面光照( specular lighting)
• 出现视觉几何无法被渲染问题，原因在于具有负的w坐标

如果从全正的对角元开始，你需要做的就是：

• 如果图像x轴和摄像机x轴指向相反方向，将 K K 的第一列以及 R R 的第一行取反
• 如果图像y轴和摄像机y轴指向相反方向，将 K K 的第二列以及 R R 的第二行取反
• 如果相机俯视是z轴负方向，将 K K 的第三列以及 R R 的第三行取反。
• 如果 R R 的行列式置为 −1 − 1 ，将它取反

以上每一步都能保证相机矩阵不变，最后一步等价于将整个相机矩阵 P P 乘以 −1 − 1 。因为 P P 的操作是基于齐次坐标系的，所以将它乘以任何的常量都无影响。

当然可以使用向量 t=−RC t = − R C 去检查结果，此式代表的是在相机坐标系中的世界坐标系原点。如果都没错，那么 tx,ty,tz t x , t y , t z 应该能够反映出在世界原点在相机中的位置(分别指出在中心左边/右边，上边/下边，相机的前面/后面)

相机矩阵求解

前面看了如何将相机矩阵分解为内参和外参矩阵的乘积。

外参矩阵

相机的外参矩阵描述的是世界坐标中相机的位置，及其指向方向。有两个成分：旋转矩阵 R R 和平移向量 t t 。它们并非恰好对应相机的旋转和平移。

外参矩阵以刚体变换矩阵的形式可以记为：左边一个 3∗3 3 ∗ 3 旋转矩阵，右边一个 3∗1 3 ∗ 1 的平移列向量

[R|t]=⎡⎣⎢r1,1r2,1r3,1r1,2r2,2r3,2r1,3r2,3r3,3|||t1t2t3⎤⎦⎥ [ R | t ] = [ r 1 , 1 r 1 , 2 r 1 , 3 | t 1 r 2 , 1 r 2 , 2 r 2 , 3 | t 2 r 3 , 1 r 3 , 2 r 3 , 3 | t 3 ]

常见的做法是在底部增加一行 (0,0,0,1) ( 0 , 0 , 0 , 1 ) ，这使得矩阵为方形的，允许我们进一步将矩阵分解为旋转和平移矩阵

[R0t1]=[I0t1]×[R001]⎡⎣⎢⎢⎢100001000010t1t2t31⎤⎦⎥⎥⎥×⎡⎣⎢⎢⎢⎢r1,1r2,1r3,10r1,2r2,2r3,20r1,3r2,3r3,300001⎤⎦⎥⎥⎥⎥ [ R t 0 1 ] = [ I t 0 1 ] × [ R 0 0 1 ] [ 1 0 0 t 1 0 1 0 t 2 0 0 1 t 3 0 0 0 1 ] × [ r 1 , 1 r 1 , 2 r 1 , 3 0 r 2 , 1 r 2 , 2 r 2 , 3 0 r 3 , 1 r 3 , 2 r 3 , 3 0 0 0 0 1 ]

这个矩阵描述的就是如何将世界坐标系中的点变换都相机坐标系中，向量 t t 描述的是世界坐标系原点在相机坐标系中的位置， R R 的列代表的是相机坐标系中世界坐标系轴的方向。

从上可以发现，外参主要作用就是描述世界坐标系到相机坐标系的转换。与我们经常想的相机坐标系到世界坐标系的转换刚好相反。

如何从相机姿态中求解外参矩阵？

实际中，直接指定相机的姿态比指定世界坐标系中的点如何转换到相机坐标系中更加自然，通过建立一个刚体变换矩阵描述相机姿态，然后对其取逆即可建立相机的外参矩阵。

因而可以这样做：定义一个描述相机中心在世界坐标系中的位置的向量 C C ，然后让 Rc R c 代表相机在世界坐标系旋转到当前姿态需要的旋转矩阵。那么描述相机姿态的变换矩阵就是 (Rc|C) ( R c | C ) 。同样在底部添加一个行向量 (0,0,0,1) ( 0 , 0 , 0 , 1 ) ，那么外参矩阵就是相机姿态矩阵的逆

[R0t1]=[Rc0C1]−1=[[I0C1][Rc001]]−1=[Rc001]−1[I0C1]−1=[RTc001][I0−C1]=[RcT0−RTcC1] [ R t 0 1 ] = [ R c C 0 1 ] − 1 = [ [ I C 0 1 ] [ R c 0 0 1 ] ] − 1 = [ R c 0 0 1 ] − 1 [ I C 0 1 ] − 1 = [ R c T 0 0 1 ] [ I − C 0 1 ] = [ R T c − R c T C 0 1 ]

倒数第三个等式变换到倒数第二个等式，使用的转置是因为 Rc R c 是正交阵，证明戳 此处 ,此外，平移矩阵的逆就是他的负数平移向量，进而可以得到外参矩阵参数和相机姿态是直接相关的：

Rt=RTc=−RC R = R c T t = − R C

不要混淆了世界坐标系的变换 R R 和相机坐标系的变换 C C

此网址有demo展示。

内参矩阵

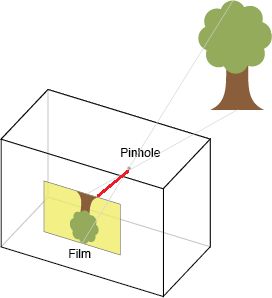
内参矩阵是将3D相机坐标变换到2D齐次图像坐标。透视投影的一个理想模型就是针孔相机。

内参矩阵如下

K=⎡⎣⎢fx00sfy0x0y01⎤⎦⎥ K = [ f x s x 0 0 f y y 0 0 0 1 ]

其中每一个参数都有实际意义。

• 表示焦距的参数: fx,fy f x , f y

  焦距就是真空与图像平面(投影屏幕)的距离，类似于人眼和视网膜，焦距的度量是针对像素的。针孔相机的 fx,fy f x , f y 有相同的值。上图中红线部分就是焦距。但是在实际中， fx f x 和 fy f y 一般不同，因为

  • 数码相机传感器的缺陷
  • 后处理中图像被非均匀缩放
  • 相机透镜导致的无意的失真
  • 相机使用了失真的格式，透镜将宽屏场景压缩到标准大小的传感器中
  • 相机校准的误差

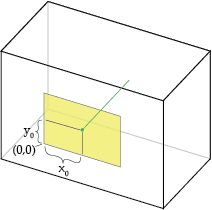
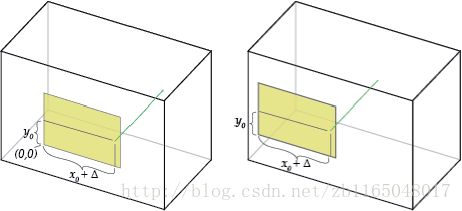
• 主点偏移 x0,y0 x 0 , y 0

  相机的主轴是与图像平面垂直且穿过真空的线，它与图像平面的焦点称为主点。

  

  主点偏移就是主点位置相对于图像平面(投影面)的位置。上图中，增加 x0 x 0 的值相当于把针孔向右移动，等价将投影面向左移动同时保持针孔位置不变。

  

• 轴倾斜

  轴倾斜会导致投影图像的形变。

• 焦距-从像素到世界单元

  内参矩阵只关心相机坐标和图像坐标之间的关系，与相机的绝对尺寸无关。针对焦距和主点偏移使用响度单元可以表示相机的相对尺寸，换句话说就是投影面的位置与其尺寸(以像素为单位)相关。

  另一种说法是内参相机变换与相机的几何均匀缩放无关，利用像素单元表示尺寸，可以捕捉到这种不变性。

  可以使用相似三角形将像素单元转换到世界单元中，前提是你知道世界单元中至少一个相机尺寸。比如你知道相机的投影面(数字传感器)宽度为 W W 毫米，图片宽度(像素为单位)为 w w ，那就可以将焦距 fx f x 转换为世界单元
  

  Fx=fxWw F x = f x W w
  
  其它的参数 fy,x0,y0 f y , x 0 , y 0 也可以被转换为对应的世界单元 Fx,X0,Y0 F x , X 0 , Y 0
  
  Fy=fyHhX0=x0WwY0=y0Hh F y = f y H h X 0 = x 0 W w Y 0 = y 0 H h

• 2D变换中的相机内参的计算

  将内参矩阵分解为切变(shear,类似于将长方形压成平行四边形的变形方式)、缩放，平移变换，分别对应轴倾斜、焦距、主点偏移
  

  K=⎡⎣⎢fx00sfy0x0y01⎤⎦⎥=⎡⎣⎢100010x0y01⎤⎦⎥×⎡⎣⎢fx000fy0001⎤⎦⎥×⎡⎣⎢⎢100sfx10001⎤⎦⎥⎥ K = [ f x s x 0 0 f y y 0 0 0 1 ] = [ 1 0 x 0 0 1 y 0 0 0 1 ] × [ f x 0 0 0 f y 0 0 0 1 ] × [ 1 s f x 0 0 1 0 0 0 1 ]
  
  第二个等式右边三个矩阵依次是：2D平移、2D缩放、2D切变

  另一种等价的分解是将切变放在缩放前面
  

  K=⎡⎣⎢100010x0y01⎤⎦⎥×⎡⎣⎢⎢100sfx10001⎤⎦⎥⎥×⎡⎣⎢fx000fy0001⎤⎦⎥ K = [ 1 0 x 0 0 1 y 0 0 0 1 ] × [ 1 s f x 0 0 1 0 0 0 1 ] × [ f x 0 0 0 f y 0 0 0 1 ]
  
  有一点需要注意：内参不影响可见性——阻隔对象(occluded objects)在图像空间中无法通过简单的2D变换显示出来。这里的occluded objects就是那些你希望看到，但是由于某些原因看不到的对象，比如目标跟踪的时候，一个目标被另一个目标遮挡了。

总结

综上可以发现相机矩阵可以通过如下方法被分解:

• 全相机矩阵被分解为内参和外参矩阵
• 外参矩阵指示3D旋转和平移
• 内参矩阵指示2D变换

整个分解方法如下

P=KIntrinsic Matrix×[R|t]Extrinsic Matrix=⎡⎣⎢100010x0y01⎤⎦⎥2D Translation×⎡⎣⎢fx000fy0000⎤⎦⎥2D Scaling×⎡⎣⎢⎢100sfx10001⎤⎦⎥⎥2D Shear×[I|t]3D Translation×[R001]3D Rotation P = K I n t r i n s i c   M a t r i x × [ R | t ] E x t r i n s i c   M a t r i x = [ 1 0 x 0 0 1 y 0 0 0 1 ] 2 D   T r a n s l a t i o n × [ f x 0 0 0 f y 0 0 0 0 ] 2 D   S c a l i n g × [ 1 s f x 0 0 1 0 0 0 1 ] 2 D   S h e a r × [ I | t ] 3 D   T r a n s l a t i o n × [ R 0 0 1 ] 3 D   R o t a t i o n

戳 此处有交互式demo

demo中提供了三种外参接口(世界坐标系，相机坐标系，look-at)，三种交互效果不同，前两种的方向相反，世界坐标系中向左移动表示相机坐标系中向右移动，但是它们都有六个参数控制:

• tx t x 表示沿着水平方向移动相机
• ty t y 表示沿着垂直方向移动相机
• tz t z 表示沿着前后方向移动相机
• px p x 表示镜头不平移，但是绕x轴做俯仰旋转
• py p y 表示镜头不平移，但是绕垂直轴y轴做左右摇头旋转
• pz p z 表示镜头不平移，但是绕z轴做顺时针(或者逆时针)旋转

demo也提供了内参的接口，包括四个参数控制：

• 焦距(Focal length):镜头的前后缩进(不是缩放)
• 轴倾斜(Axis Skew):可以导致球变形，平面上显示椭球形
• x0 x 0 表示主点偏移，相机不动，左右移动成像平面
• y0 y 0 表示主点偏移，相机不动，上下移动成像平面