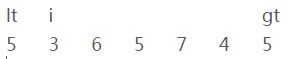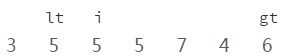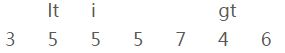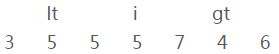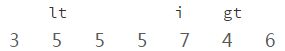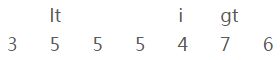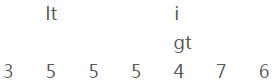【算法理解】—— 快速排序（三向切分）

前言

    大家好，依然是天灾依然是随机。本来打算上周末写，但是谁知道上周各种加班，各种忙成汪…终于闲下来，于是开始介绍另一篇之前学习过的算法。


    写这篇博文的目的有两个：
        1、在上一篇博文中，并没有针对“快速算法”做一个简单的介绍，所以这里做一个补充；
        2、想让大家理解一句话：没有最好的算法，只有在不同情况下存在最好的算法。


    另外，我收到了邮件的反馈，关于我上篇博文的建议。所以我打算在本篇博文改进一下思路。如果有不合适的地方，可以发邮件到我的QQ邮箱，我会第一时间回复，并进一步改善自己的写作思路。


    废话不多说，进入正文。

算法介绍

    在我的上一篇博文中，介绍了“快速排序”算法的整个运行流程。但是并没有针对该算法做一个简单的介绍。所以在本博文中，针对“快速排序”进行一个补充介绍。

关于“快速排序”的理解，请戳这里 http://blog.csdn.net/a8336675/article/details/

    首先，一个算法的好坏的决定因素主要有两点：
        1、运行所需要的内存空间；
        2、运行所需要的时间。


    那么关于“快速排序”算法的优缺点如下：
        优点：
            1、原地排序（只需要一个很小的辅助栈，内存消耗小）；
                因为该算法主要是通过交换“比参照物大的数值”和“比参照物小的数值”来实现排序。除了记录“左右指针”以外，仅仅在交换位置的时候，创建了一个变量；

            2、排序一个长度为N的数组，所需的时间和【NlgN】成正比，所需耗时的增长数量级为“线性对数级别”（关于增长耗时的增长数量级，本人打算另写一篇博文，关于该概念的理解）。

            3、内循环比大多数排序算法都要短小，例如：
            选择排序需要循环N-1-i（i表示外循环的变量）次，才能完成一次内循环；
            而快速排序的内循环次数，根据数组的有序程度而定。区间在1 ~ N / 2 - 1的范围内。

        缺点：非常脆弱，编写时容易出现错误，导致实际性能只有“平方级别”。

以上是本人针对官方说明的理解，下面用一张图来表示“快速排序”的优势：

上面是各种主流排序算法针对于100W条随机数据进行排序的耗时，由此可见“快速排序”果然法如其名。

别问我“选择排序”和“插入排序”去哪了，我跑了5分钟，没出结果，最后放弃了。

好了，到这里就是关于快速排序的介绍。那么快速排序已经这么NB了，为啥还需要优化？
某位伟人曾今说过：没有最好的算法，只有在不同情况下存在最好的算法。（别问我是谁说的，再问自杀）

数学家们发现，虽然快速排序已经很快了，但是在一种情况下存在可以优化的余地：【数组中存在大量重复数据】。
因为，“左右指针”分别找“比参照物大的元素”和“比参照物小的元素”，所以“等于参照物的元素”就原封不动的放在原地，在下一级迭代排序中继续参与排序。

这时候，天空一声巨响，快速排序（三向切分）横空出世。

算法源码

    在上一篇博文中，由于本人不大会用CSDN的编辑器，采用了截图的方式，但是有博友发邮件跟我说，代码不能Copy…（虽然我很想说，身为一名Code Generator不能天天Copy code。但是为了各位博友的方便，在下闭关学习编辑器的使用，目前略有小成）。

    /**
     * 快速排序
     */
    private static void sort(Comparable[] arr) {
        sort_three_split(arr, 0, arr.length - 1);
    }

    /**
     * 三向切分的快速排序
     * 
     * @param arr
     * @param begin
     * @param end
     */
    private static void sort_three_split(Comparable[] arr, int begin, int end) {
a、      if (begin >= end) return;

        // 1, 获取参照物
b、      Comparable refer = arr[begin];

        // 2, 记录“少于”、“多余”下标
c、      int i = begin + 1, lt = begin, gt = end;

        // 3, 开始计算需要进行迭代的位置
d、      while (i <= gt) {
    i、      int result = arr[i].compareTo(refer);
    ii、     if (result > 0) swap(arr, i, gt--);       // 当前元素大于参照物
    iii、    else if (result < 0) swap(arr, i++, lt++);// 当前元素小于参照物
    iv、     else i++;                                 // 当前元素等于参照物
        }

        // 4, 最终迭代比较“小于参照物”的部分和“大于参照物”的部分
e、      sort_three_split(arr, begin, lt - 1);
f、      sort_three_split(arr, gt + 1, end);
    }

代码就这么多，上面的 a-f 的标记，是为了接下来讲解方便加上的，别问我为什么程序运行不了…

算法理解

    接下来，咱们对快速排序（三向切分）进行分步讲解。各位同学别急着看上面的代码，跟着在下的节奏往下走。

a、迭代结束判断，如果迭代到了只剩余1个元素，无需继续进行下面操作，防止死循环；

b、跟快速排序一样，使用当前排序部分的第一个元素作为参照物；

c、这里与快速排序不一样了。
        快速排序中仅记录了“左右指针”；
        这里记录了“小于参照物的指针”【lt】、“大于参照物的指针”【gt】，以及“当前指针”【i】。
        这里的三个指针分别是有什么用呢？ 让我们往下看。

d、开始进行“分类”操作
        i、获取当前值和参照物比较的结果；
        ii、如果当前的值arr[I]大于参照物，交换当前值的位置【i】和【gt】的位置（先别急，暂时理解为把较大的值，放到数组的后端）；
        iii、如果当前的值arr[I]小于参照物，交换当前值的位置【i】和【lt】的位置（暂时理解为把较小的值，放到数组的前端）；
        iv、如果当前的值arr[I]等于参照物，则将当前值的指针【i】的位置后移一位。

e、迭代排序位置begin到位置lt + 1的部分；

f、迭代排序位置gt + 1到位置end的部分。

算法分析

        // 4, 最终迭代比较“小于参照物”的部分和“大于参照物”的部分
e、      sort_three_split(arr, begin, lt - 1);
f、      sort_three_split(arr, gt + 1, end);

首先，看一下流程e和f。这两段代码和快速排序中的最后两段代码几乎一致，就是下标稍微有点变化：
        1、快速排序中，仅有一个下标【j】。然后对【j】的左边部分，和【j】的右边部分分别进行下一级迭代排序；
        2、而这里，有两个下标【lt】和【gt】。分别对【lt】左边的部分、【gt】右边的部分进行下一级迭代排序。

首先，我们能够得出结论：“【lt】左边的元素不大于参照物，【gt】右边的元素不小于参照物”。
因为，根据上面代码，没有针对【lt】位置到【gt】（包括【lt】和【gt】）的部分进行下一级的排序，如果不符合上面推断出来的结论，那么该算法并不能达到排序效果。

然后，通过上面的结论，我们能够推出另外一个“待证实”的结论：
“下标【lt】到下标【gt】的部分（包括【lt】和【gt】），所有元素的值相等。”
原因如下：
    1、【lt】左边的元素不大于参照物，【gt】右边的元素不小于参照物。但是，这也有可能等于参照物；
    2、根据本博文的命题，快速排序三向切分算法，就是为了解决对等于参照物的元素，做不必要的向下迭代排序的问题。

不过上面的结论仅仅是猜测，并不能作为正式的结论。

        // 1, 获取参照物
b、      Comparable refer = arr[begin];

        // 2, 记录“少于”、“多余”下标
c、      int i = begin + 1, lt = begin, gt = end;

        // 3, 开始计算需要进行迭代的位置
d、      while (i <= gt) {
    i、      int result = arr[i].compareTo(refer);
    ii、     if (result > 0) swap(arr, i, gt--);       // 当前元素大于参照物
    iii、    else if (result < 0) swap(arr, i++, lt++);// 当前元素小于参照物
    iv、     else i++;                                 // 当前元素等于参照物
        }

别着急，接下来咱们分析流程b、流程c和流程d。

流程b，将数组当前部分（arr[begin] 到 arr[end]）的第一个元素作为参照物。

流程c，将数组当前部分（arr[begin] 到 arr[end]）的第一个元素的下标begin，作为【lt】的值；
        将当前部分的最后一个元素的下标end，作为【gt】的值；
        最后将数组当前部分的第二个元素的下标，作为【i】的值。

        仅仅看这里，并不能理解【i】、【gt】和【lt】下标的意义。所以咱们接着向下看。

流程d，当【i】小于等于【gt】时，继续循环进行“分类”操作。
        流程i、记录当前位置【i】的值和参照物的比较结果；
        流程ii、当前位置【i】的元素大于参照物的时候，交换【i】和【gt】的位置，然后将【gt】向左移动一位。
                这里的操作类似于插入排序的操作，先将【i】和【gt】替换之后，【gt】再左移动一位。
                就相当于将“比参照物大的元素”插入数组的尾部。

                但是注意，如果是单纯的将元素插入数组尾部，需要将当前位置【i】之后的一共gt - i个元素，全部向前移动一位；而此处仅仅移动了两个元素的位置，相对于插入排序，大大减少了对数组的操作次数。

                另外，之所以将【gt】向左移动一位的原因是：
                交换数据之后，此时【gt】位置所代表的是大于参照物的值，并且已经放到数组尾部。所以不用参与接下来的“分类”操作，故将【gt】向左移动一位。

        流程iii、当位置【i】的元素小于参照物的时候，交换【i】和【lt】的位置，然后将【lt】和【i】向右移动一位。

                同样类似于插入排序，相当于将“比参照物小的元素”插入数组的前端。

                之所以将【lt】和【i】都向右移动一位的原因是：
                交换数据之后，此时【lt】位置所代表的元素是小于参照物的值。所以该值不用参与接下来的“分类”操作，故将【lt】向右移动一位。

                * 命题：【lt】恒指向第一个等于参照物的元素。该命题将在下面的举例说明中验证。

                此时【i】和【lt】在同一个元素上，所以根据上面的命题，【i】指向的是参照物，所以【i】需要向右移动一位（没有必要将参照物与参照物进行对比）。

        流程iv、当参照物与【i】指向的元素的值相等时，仅将【i】向右移动一位。这样，便将等于参照物的元素“分类”到一起。

分析到这里，就结束了。接下来将举例帮大家进一步理解，建议大家可以看完举例之后，再回来消化一下，效果更好。

举例说明

由于上一篇博客中，有博友留言说手机客户端的排版格式出现错乱，所以下面采用截图的方式做图例说明。

举例数组：{ 5， 3， 6， 5， 7， 4， 5}

注意：请记住上面的命题，观察【lt】是否恒指向第一个等于参照物的元素。

        // 1, 获取参照物
b、      Comparable refer = arr[begin];

        // 2, 记录“少于”、“多余”下标
c、      int i = begin + 1, lt = begin, gt = end;

        // 3, 开始计算需要进行迭代的位置
d、      while (i <= gt) {
    i、      int result = arr[i].compareTo(refer);
    ii、     if (result > 0) swap(arr, i, gt--);       // 当前元素大于参照物
    iii、    else if (result < 0) swap(arr, i++, lt++);// 当前元素小于参照物
    iv、     else i++;                                 // 当前元素等于参照物
        }

经过b、c流程之后，结构应该如下所示：

———————————— 第一轮循环 ————————————
i、当前元素[3]和参照物[5]进行比较，比参照物要小；

iii、交换【i】和【lt】的位置

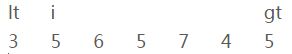
    并且【lt】和【i】都向右移一位

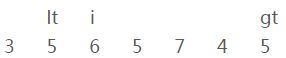
———————————— 第二轮循环 ————————————
i、当前元素[6]和参照物[5]（上图）进行比较，比参照物要大；

ii、交换【i】和【gt】的位置，

    并且【gt】向左移一位

———————————— 第三轮循环 ————————————
i、当前元素[5]和参照物[5]（上图）进行比较，等于参照物；

iv、【i】向右移动一位

———————————— 第四轮循环 ————————————
i、当前元素[5]和参照物[5]（上图）进行比较，等于参照物；

iv、【i】向右移动一位

———————————— 第五轮循环 ————————————
i、当前元素[7]和参照物[5]（上图）进行比较，比参照物要大；

ii、交换【i】和【gt】的位置，

    并且【gt】向左移一位

———————————— 第六轮循环 ————————————
i、当前元素[4]和参照物[5]（上图）进行比较，比参照物要小；

iii、交换【i】和【lt】的位置

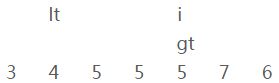
    并且【lt】和【i】都向右移一位

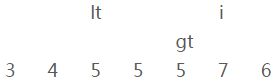
———————————— 第七轮循环 ————————————
由于【i】已经大于【gt】，所以跳出循环。最终结果如下：

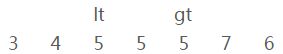
运行到这里，大家可以看到，【lt】左边的数据恒比参照物小，【gt】右边的数据恒比参照物大。

除此之外，还验证了上面关于“下标【lt】到下标【gt】的部分（包括【lt】和【gt】的元素），所有元素的值相等”的猜测。

总结

    接下来，把上面的内容稍微梳理一下。

private static void sort_three_split(Comparable[] arr, int begin, int end) {
a、      if (begin >= end) return;

        // 1, 获取参照物
b、      Comparable refer = arr[begin];

        // 2, 记录“少于”、“多余”下标
c、      int i = begin + 1, lt = begin, gt = end;

        // 3, 开始计算需要进行迭代的位置
d、      while (i <= gt) {
    i、      int result = arr[i].compareTo(refer);
    ii、     if (result > 0) swap(arr, i, gt--);       // 当前元素大于参照物
    iii、    else if (result < 0) swap(arr, i++, lt++);// 当前元素小于参照物
    iv、     else i++;                                 // 当前元素等于参照物
        }

        // 4, 最终迭代比较“小于参照物”的部分和“大于参照物”的部分
e、      sort_three_split(arr, begin, lt - 1);
f、      sort_three_split(arr, gt + 1, end);
    }

a、当开始位置begin不小于结束位置end的时候，说明已经只有一个元素，直接返回不进行排序；
b、使用数组当前部分（begin - end）的第一个元素作为参照物；
c、使用begin位置作为【lt】下标，使用end位置作为【gt】下标，并使用begin+1作为【i】下标；
        因为【lt】左侧是比参照物小的值，所以使用begin作为初始值，因为初始化的时候并没有比参照物小的值；
        而【gt】右侧是比参照物大的值，所以使用end作为初始值，因为初始化的时候并没有比参照物大的值。
        而【i】表示需要与参照物比较的元素，所以从参照物之后的第一个元素开始。

d、当【i】第一次大于【gt】的时候，也就是【gt + 1】的位置。由于【gt】的右侧全部是大于参照物的值，所以没必要进行“分类”操作了。所以当【i <= gt】的时候，才需要继续进行“分类”操作；
        i、记录当前值和参照物的比较结果；
        ii、当 当前值 大于参照物时，将当前的值置换到数组的前端部分；
            之后将【lt】的位置向右移动一位，让【lt】重新指向参照物；
            再将【i】向右移动一位，避免和【lt】重合（因为【lt】指向的是参照物）
        iii、当 当前值 小于参照物时，将当前值置换到数组的末端部分；
            之后将【gt】的位置向左移动一位，因为当前【gt】指向的是“大于参照物的值”；
            这里【i】并不移动的原因，是因为把“比参照物大的值”和【gt】进行置换，
            但是此时并不知道原来【gt】位置的值比参照物大还是小，所以需要将该值进行比较。
        iv、当 当前值 等于参照物的值时，仅将【i】向右移动一位。
            这也是该算法相对于快速排序最关键的不同点，这样将等于参照物的值和参照物连接在一起。

e、对【lt】左边的部分（小于参照物的部分）进行下一级“分类”操作，分类操作到了最后仅剩2~3个元素的时候，实际加上就是排序；

f、对【gt】右边的部分（大于参照物的部分）进行下一级“分类”操作。

上面的d流程总结的比较复杂，实际上用一句话能概括其中心思想：
将比参照物小的放到数组左端，将比参照物大的放到数组右端，将等于参照物的元素与参照物放在一起。

这样，等于参照物的元素就不用参与下一级的“分类”操作，降低了“分类”的操作次数，提高了快速排序的性能。

试验结果

我先喝口水…
终于分析完了，此时此刻早已泪流满面。

按耐不住自己鸡冻的心情，写好了Demo准备运行。一运行…

纳尼… 我又运行了十几次，结果依然和上图一致（数值不同，结果相同）。

然后我花了20分钟检查自己的代码，一行一行跟源码进行比对，想着哪里写错了。结果并木有写错。

最后我把源代码Copy过来一运行，结果竟然还是一样…

WTF ? ! 这跟说好的不一样啊！说好的优化呢？！

我出去吃了半边西瓜冷静了一下，想了慢慢看了看资料。发现了问题：
我创建了100W条在数值范围在0 - 500W之间的随机数组，但是当前算法的优化方案针对的是有大量重复数据的情况下进行的优化。

于是，我默默的将区间设置为0 - 50，然后再一运行：

再一次，我泪流满面…

运行结果分析

虽然我们得到了自己想要的结果，但是，为什么数据不一样的时候，运行耗时差距这么大呢？

问题的关键，就在于快速排序和快速排序（三向切分）的“分类”机制略微不同：
    1、快速排序，“左右指针”找到位置之后，仅进行一次交换，便将“比参照物小的元素”放到前端以及将“比参照物大的元素”放到的末端；

    2、三向切分，【gt】指针和【i】交换，仅仅将“比参照物大的元素”放到了末端，但是交换的另外一个值（原来在【gt】位置的元素的值），并不知道该值的大小，需要再循环一次判断该值的大小。所以仅仅将【gt】向左移动一位，而【i】依然在原来的位置。

从上面不难看出，在没有重复内容的数组中，三向切分的数组交换次数要比快速算法多得多。

所以，“快速排序（三向切分）”算法仅适用于重复值较多的数组。例如：
针对于性别、年龄、薪资等重复较多的数据进行排序。

作者感言

    通过上面的运行结果的分析，也刚好验证了上面那个不知名的伟人说过的话：“没有最好的算法，只有在不同情况下存在最好的算法”。要想设计一个合适的算法，我们必须了解每一个算法它们的优劣势，并根据数据的内容（重复内容的比率，数组的长度等因素）来设计。

    不知不觉已经天黑了，站起来动了动胳膊，穿上衣服出去觅食。走到楼下，抬头仰望星空，眉头紧锁，长叹一口气：马丹，忘带钥匙了…

    最后，各位博友针对本博文有什么问题，随时欢迎发邮件到我的QQ邮箱，或者下方留言。本人会及时回复，大家相互讨论。

邮箱：[email protected]