机器学习实战笔记(六):Logistic回归(Python3 实现)
1 Logistic回归介绍
假设现在有一些数据点,我们用一条直线对这些点进行拟合(该线称为最佳拟合直线),这个拟合过程就称作回归。利用Logistic回归进行分类的主要思想是:根据现有数据对分类边界线建立回归公式,以此进行分类。这里的“回归”一词源于最佳拟合,表示要找到最佳拟合参数集。训练分类器时的做法就是寻找最佳拟合参数,使用的是最优化算法。
1.1 Logistic回归的一般过程(1) 收集数据:采用任意方法收集数据。
(2) 准备数据:由于需要进行距离计算,因此要求数据类型为数值型。另外,结构化数据格式则最佳。
(3) 分析数据:采用任意方法对数据进行分析。
(4) 训练算法:大部分时间将用于训练,训练的目的是为了找到最佳的分类回归系数。
(5) 测试算法:一旦训练步骤完成,分类将会很快。
(6) 使用算法:首先,我们需要输入一些数据,并将其转换成对应的结构化数值;接着,基于训练好的回归系数就可以对这些数值进行简单的回归计算,判定它们属于哪个类别;在这之后,我们就可以在输出的类别上做一些其他分析工作。
2 基于 Logistic 回归和 Sigmoid 函数的分类
2.1 Logistic回归特点优点:计算代价不高,易于理解和实现。
缺点:容易欠拟合,分类精度可能不高。
适用数据类型:数值型和标称型数据。
import numpy as np
# Logistic 回归梯度上升优化算法
def load_data_set():
# 创建两个列表
data_mat = []
label_mat = []
fr = open('testSet.txt')
for line in fr.readlines():
# 对当前行去除首尾空格,并按空格进行分离
line_arr = line.strip().split()
data_mat.append([1.0, float(line_arr[0]), float(line_arr[1])])
label_mat.append(int(line_arr[2]))
return data_mat, label_mat
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
# return 0.5 * (1 + np.tanh(0.5 * inx))
def grad_ascent(data_mat_in, class_labels):
data_matrix = np.mat(data_mat_in) # convert to NumPy matrix
label_mat = np.mat(class_labels).transpose() # convert to NumPy matrix
m, n = np.shape(data_matrix)
alpha = 0.001
max_cycles = 500
weights = np.ones((n, 1))
for k in range(max_cycles): # heavy on matrix operations
h = sigmoid(data_matrix * weights) # matrix mult
error = (label_mat - h) # vector subtraction
weights = weights + alpha * data_matrix.transpose() * error # matrix mult
return weights2.2 分析数据:画出决策边界
# 画出数据集和Logistic回归最佳拟合直线的函数
def plot_best_fit(weights):
import matplotlib.pyplot as plt
data_mat, label_mat = load_data_set()
data_arr = np.array(data_mat)
n = np.shape(data_arr)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(label_mat[i]) == 1:
xcord1.append(data_arr[i, 1])
ycord1.append(data_arr[i, 2])
else:
xcord2.append(data_arr[i, 1])
ycord2.append(data_arr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()if __name__ == '__main__':
dataMat, labelMat = load_data_set()
weights = grad_ascent(dataMat, labelMat)
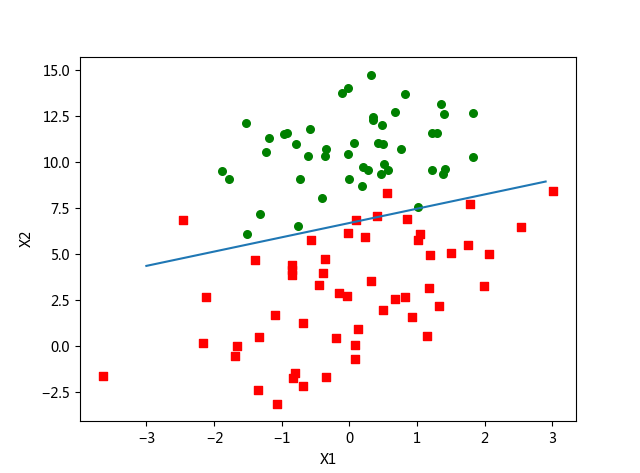
plot_best_fit(weights.getA())这个分类结果相当不错,从图上看只错分了两到四个点。但是,尽管例子简单且数据集很小,这个方法却需要大量的计算(300次乘法)。因此下一节将对该算法稍作改进,从而使它可以用在真实数据集上。
2.3 训练算法:随机梯度上升
梯度上升算法在每次更新回归系数时都需要遍历整个数据集,该方法在处理100个左右的数
据集时尚可,但如果有数十亿样本和成千上万的特征,那么该方法的计算复杂度就太高了。一种
改进方法是一次仅用一个样本点来更新回归系数,该方法称为随机梯度上升算法。由于可以在新
样本到来时对分类器进行增量式更新,因而随机梯度上升算法是一个在线学习算法。与“在线学
习”相对应,一次处理所有数据被称作是“批处理”。
随机梯度上升算法可以写成如下的伪代码:
所有回归系数初始化为1
对数据集中每个样本
计算该样本的梯度
使用alpha × gradient更新回归系数值
返回回归系数值
以下是随机梯度上升算法的实现代码。
def stoc_grad_ascent0(data_matrix, class_labels):
m, n = np.shape(data_matrix)
alpha = 0.01
weights = np.ones(n) # initialize to all ones
for i in range(m):
h = sigmoid(sum(data_matrix[i] * weights))
error = class_labels[i] - h
weights = weights + alpha * error * data_matrix[i]
return weightsif __name__ == '__main__':
dataMat, labelMat = load_data_set()
weights = stoc_grad_ascent0(np.array(dataMat), labelMat)
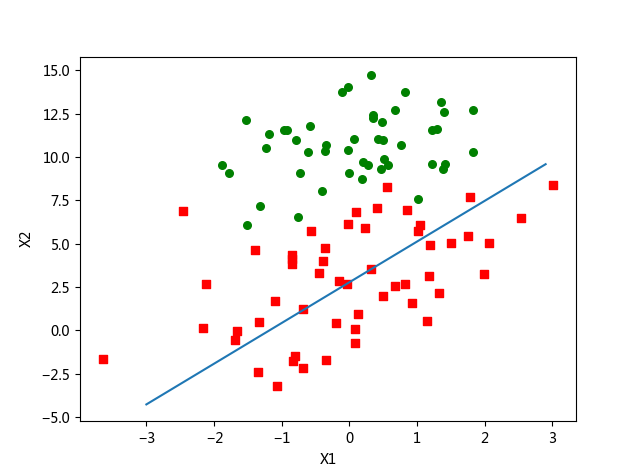
plot_best_fit(weights)执行完毕后将得到图2所示的最佳拟合直线图,该图与图1有一些相似之处。可以看到,拟合出来的直线效果还不错,但并不像图1那样完美。这里的分类器错分了三分之一的样本。
图2
# 改进的随机梯度上升算法
def stoc_grad_ascent1(data_matrix, class_labels, num_iter=150):
m, n = np.shape(data_matrix)
weights = np.ones(n) # initialize to all ones
for j in range(num_iter):
data_index = list(range(m))
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.0001 # apha decreases with iteration, does not
rand_index = int(np.random.uniform(0, len(data_index))) # go to 0 because of the constant
h = sigmoid(sum(data_matrix[rand_index] * weights))
error = class_labels[rand_index] - h
weights = weights + alpha * error * data_matrix[rand_index]
del (data_index[rand_index])
return weightsif __name__ == '__main__':
dataMat, labelMat = load_data_set()
weights = stoc_grad_ascent1(np.array(dataMat), labelMat)
plot_best_fit(weights)3 示例:从疝气病症预测病马的死亡率
3.1 使用Logistic回归估计马疝病的死亡率过程(1) 收集数据:给定数据文件。
(2) 准备数据:用Python解析文本文件并填充缺失值。
(3) 分析数据:可视化并观察数据。
(4) 训练算法:使用优化算法,找到最佳的系数。
(5) 测试算法:为了量化回归的效果,需要观察错误率。根据错误率决定是否回退到训练阶段,通过改变迭代的次数和步长等参数来得到更好的回归系数。
3.2 准备数据:处理数据中的缺失值
数据中的缺失值是个非常棘手的问题,有很多文献都致力于解决这个问题。那么,数据缺失究竟带来了什么问题?假设有100个样本和20个特征,这些数据都是机器收集回来的。若机器上的某个传感器损坏导致一个特征无效时该怎么办?此时是否要扔掉整个数据?这种情况下,另外19个特征怎么办?它们是否还可用?答案是肯定的。因为有时候数据相当昂贵,扔掉和重新获取都是不可取的,所以必须采用一些方法来解决这个问题。
下面给出了一些可选的做法:
使用可用特征的均值来填补缺失值;
使用特殊值来填补缺失值,如-1;
忽略有缺失值的样本;
使用相似样本的均值添补缺失值;
使用另外的机器学习算法预测缺失值。
3.3 测试算法:用 Logistic 回归进行分类
使用Logistic回归方法进行分类并不需要做很多工作,所需做的只是把测试集上每个特征向量乘以最优化方法得来的回归系数,再将该乘积结果求和,最后输入到Sigmoid函数中即可。如果对应的Sigmoid值大于0.5就预测类别标签为1,否则为0。
# Logistic回归分类函数
def classify_vector(inx, weights):
"""
它以回归系数和特征向量作为输入来计算对应的Sigmoid值。
如果Sigmoid值大于0.5函数返回1,否则返回0。
"""
prob = sigmoid(sum(inx * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def colic_test():
fr_train = open('horseColicTraining.txt')
fr_test = open('horseColicTest.txt')
training_set = []
training_labels = []
for line in fr_train.readlines():
curr_line = line.strip().split('\t')
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
training_set.append(line_arr)
training_labels.append(float(curr_line[21]))
train_weights = stoc_grad_ascent1(np.array(training_set), training_labels, 1000)
error_count = 0
num_test_vec = 0.0
for line in fr_test.readlines():
num_test_vec += 1.0
curr_line = line.strip().split('\t')
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
if int(classify_vector(np.array(line_arr), train_weights)) != int(curr_line[21]):
error_count += 1
error_rate = (float(error_count) / num_test_vec)
print("the error rate of this test is: %f" % error_rate)
return error_rate
def multi_test():
num_tests = 10
error_sum = 0.0
for k in range(num_tests):
error_sum += colic_test()
print("after %d iterations the average error rate is: %f" % (num_tests, error_sum / float(num_tests)))if __name__ == '__main__':
# dataMat, labelMat = load_data_set()
# weights = grad_ascent(dataMat, labelMat)
# weights = stoc_grad_ascent1(np.array(dataMat), labelMat)
# plot_best_fit(weights)
multi_test()输出结果:
D:\ProgramData\Anaconda2\envs\python3\python.exe E:/study_code/ML_in_action_code/logistic_regression/logRegres.py
E:/study_code/ML_in_action_code/logistic_regression/logRegres.py:27: RuntimeWarning: overflow encountered in exp
return 1.0 / (1 + np.exp(-inx))
the error rate of this test is: 0.328358
the error rate of this test is: 0.298507
the error rate of this test is: 0.313433
the error rate of this test is: 0.358209
the error rate of this test is: 0.313433
the error rate of this test is: 0.253731
the error rate of this test is: 0.417910
the error rate of this test is: 0.313433
the error rate of this test is: 0.253731
the error rate of this test is: 0.298507
after 10 iterations the average error rate is: 0.314925
Process finished with exit code 0从上面的结果可以看到, 10次迭代之后的平均错误率为31%。事实上,这个结果并不差,因为有30%的数据缺失。当然,如果调整colic_test()中的迭代次数和stoch_grad_ascent1()中的步长,平均错误率可以降到20%左右。
注意:运行中有个警告:
RuntimeWarning: overflow encountered in expreturn 1.0 / (1 + np.exp(-inx)),可以转换成如下等价形式后算法会更稳定:return 0.5 * (1 + np.tanh(0.5 * x)) 参考《基于RBM的推荐算法》
3.4 完整代码
# encoding: utf-8
"""
@author:max bay
@version: python 3.6
@time: 2018/6/2 20:55
"""
import numpy as np
# Logistic 回归梯度上升优化算法
def load_data_set():
# 创建两个列表
data_mat = []
label_mat = []
fr = open('testSet.txt')
for line in fr.readlines():
# 对当前行去除首尾空格,并按空格进行分离
line_arr = line.strip().split()
data_mat.append([1.0, float(line_arr[0]), float(line_arr[1])])
label_mat.append(int(line_arr[2]))
return data_mat, label_mat
def sigmoid(inx):
return 1.0 / (1 + np.exp(-inx))
# return 0.5 * (1 + np.tanh(0.5 * inx))
def grad_ascent(data_mat_in, class_labels):
data_matrix = np.mat(data_mat_in) # convert to NumPy matrix
label_mat = np.mat(class_labels).transpose() # convert to NumPy matrix
m, n = np.shape(data_matrix)
alpha = 0.001
max_cycles = 500
weights = np.ones((n, 1))
for k in range(max_cycles): # heavy on matrix operations
h = sigmoid(data_matrix * weights) # matrix mult
error = (label_mat - h) # vector subtraction
weights = weights + alpha * data_matrix.transpose() * error # matrix mult
return weights
# 画出数据集和Logistic回归最佳拟合直线的函数
def plot_best_fit(weights):
import matplotlib.pyplot as plt
data_mat, label_mat = load_data_set()
data_arr = np.array(data_mat)
n = np.shape(data_arr)[0]
xcord1 = []
ycord1 = []
xcord2 = []
ycord2 = []
for i in range(n):
if int(label_mat[i]) == 1:
xcord1.append(data_arr[i, 1])
ycord1.append(data_arr[i, 2])
else:
xcord2.append(data_arr[i, 1])
ycord2.append(data_arr[i, 2])
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(xcord1, ycord1, s=30, c='red', marker='s')
ax.scatter(xcord2, ycord2, s=30, c='green')
x = np.arange(-3.0, 3.0, 0.1)
y = (-weights[0] - weights[1] * x) / weights[2]
ax.plot(x, y)
plt.xlabel('X1')
plt.ylabel('X2')
plt.show()
def stoc_grad_ascent0(data_matrix, class_labels):
m, n = np.shape(data_matrix)
alpha = 0.01
weights = np.ones(n) # initialize to all ones
for i in range(m):
h = sigmoid(sum(data_matrix[i] * weights))
error = class_labels[i] - h
weights = weights + alpha * error * data_matrix[i]
return weights
# 改进的随机梯度上升算法
def stoc_grad_ascent1(data_matrix, class_labels, num_iter=150):
m, n = np.shape(data_matrix)
weights = np.ones(n) # initialize to all ones
for j in range(num_iter):
data_index = list(range(m))
for i in range(m):
alpha = 4 / (1.0 + j + i) + 0.0001 # apha decreases with iteration, does not
rand_index = int(np.random.uniform(0, len(data_index))) # go to 0 because of the constant
h = sigmoid(sum(data_matrix[rand_index] * weights))
error = class_labels[rand_index] - h
weights = weights + alpha * error * data_matrix[rand_index]
del (data_index[rand_index])
return weights
# Logistic回归分类函数
def classify_vector(inx, weights):
"""
它以回归系数和特征向量作为输入来计算对应的Sigmoid值。
如果Sigmoid值大于0.5函数返回1,否则返回0。
"""
prob = sigmoid(sum(inx * weights))
if prob > 0.5:
return 1.0
else:
return 0.0
def colic_test():
fr_train = open('horseColicTraining.txt')
fr_test = open('horseColicTest.txt')
training_set = []
training_labels = []
for line in fr_train.readlines():
curr_line = line.strip().split('\t')
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
training_set.append(line_arr)
training_labels.append(float(curr_line[21]))
train_weights = stoc_grad_ascent1(np.array(training_set), training_labels, 1000)
error_count = 0
num_test_vec = 0.0
for line in fr_test.readlines():
num_test_vec += 1.0
curr_line = line.strip().split('\t')
line_arr = []
for i in range(21):
line_arr.append(float(curr_line[i]))
if int(classify_vector(np.array(line_arr), train_weights)) != int(curr_line[21]):
error_count += 1
error_rate = (float(error_count) / num_test_vec)
print("the error rate of this test is: %f" % error_rate)
return error_rate
def multi_test():
num_tests = 10
error_sum = 0.0
for k in range(num_tests):
error_sum += colic_test()
print("after %d iterations the average error rate is: %f" % (num_tests, error_sum / float(num_tests)))
if __name__ == '__main__':
# dataMat, labelMat = load_data_set()
# weights = grad_ascent(dataMat, labelMat)
# weights = stoc_grad_ascent1(np.array(dataMat), labelMat)
# plot_best_fit(weights)
multi_test()4 总结
Logistic回归的目的是寻找一个非线性函数Sigmoid的最佳拟合参数,求解过程可以由最优化算法来完成。在最优化算法中,最常用的就是梯度上升算法,而梯度上升算法又可以简化为随机梯度上升算法。
随机梯度上升算法与梯度上升算法的效果相当,但占用更少的计算资源。此外,随机梯度上升是一个在线算法,它可以在新数据到来时就完成参数更新,而不需要重新读取整个数据集来进行批处理运算。
机器学习的一个重要问题就是如何处理缺失数据。这个问题没有标准答案,取决于实际应用中的需求。现有一些解决方案,每种方案都各有优缺点。
5 参考及阅读资料
[1] 机器学习实战
[2] 机器学习实战之logistic回归
[3] Python3《机器学习实战》学习笔记(六):Logistic回归基础篇之梯度上升算法
[4] Python3《机器学习实战》学习笔记(七):Logistic回归实战篇之预测病马死亡率
[5] python机器学习实战 getA()函数详解
[6] python3中报错:TypeError: 'range' object doesn't support item deletion
[7] 机器学习4logistic回归