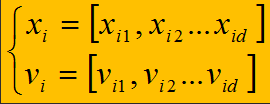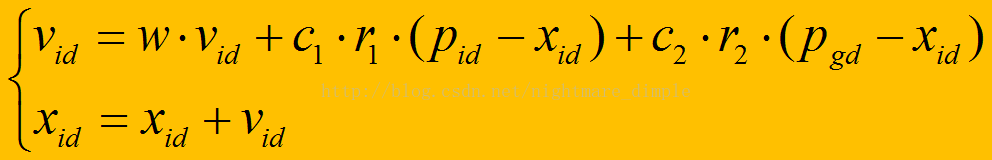粒子群算法的matlab实现(一)
粒子群算法(Particle Swarm Optimization,PSO)是20世纪90年代兴起的一门学科,因其概念简明、实现方便、收敛速度快而为人所知。粒子群算法的基本思想是模拟鸟群随机搜寻食物的捕食行为,鸟群通过自身经验和种群之间的交流调整自己的搜寻路径,从而找到食物最多的地点。其中每只鸟的位置/路径则为自变量组合,每次到达的地点的食物密度即函数值。每次搜寻都会根据自身经验(自身历史搜寻的最优地点)和种群交流(种群历史搜寻的最优地点)调整自身搜寻方向和速度,这个称为跟踪极值,从而找到最优解。
粒子群算法是一门新兴算法,此算法与遗传算法有很多相似之处,其收敛于全局最优解的概率很大。
①相较于传统算法计算速度非常快,全局搜索能力也很强;
②PSO对于种群大小不十分敏感,所以初始种群设为500-1000,速度影响也不大;
③粒子群算法适用于连续函数极值问题,对于非线性、多峰问题均有较强的全局搜索能力。
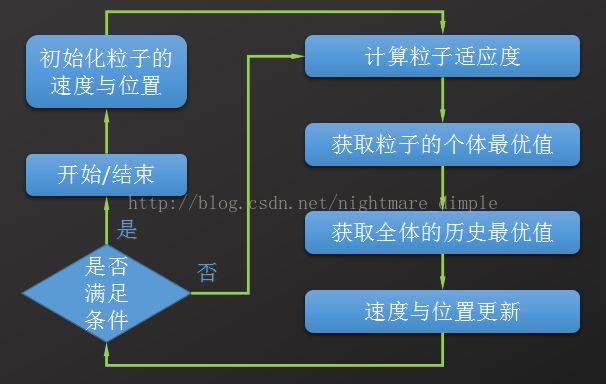
其流程图如下:
Step1:确定一个粒子的运动状态是利用位置和速度两个参数描述的,因此初始化的也是这两个参数;
Step2:
每次搜寻的结果(函数值)即为粒子适应度,然后记录每个粒子的个体历史最优位置和群体的历史最优位置;
Step3:
个体历史最优位置和群体的历史最优位置相当于产生了两个力,结合粒子本身的惯性共同影响粒子的运动状态,由此来更新粒子的位置和速度。
粒子群算法中所涉及到的参数有:
种群数量:粒子群算法的最大特点就是速度快,因此初始种群取50-1000都是可以的,虽然初始种群越大收敛性会更好,不过太大了也会影响速度;
迭代次数:一般取100~4000,太少解不稳定,太多浪费时间。对于复杂问题,进化代数可以相应地提高;
惯性权重:该参数反映了个体历史成绩对现在的影响,一般取0.5~1;
学习因子:一般取0~4,此处要根据自变量的取值范围来定,并且学习因子分为个体和群体两种;
迭代次数:一般取100~4000,太少解不稳定,太多浪费时间。对于复杂问题,进化代数可以相应地提高;
惯性权重:该参数反映了个体历史成绩对现在的影响,一般取0.5~1;
学习因子:一般取0~4,此处要根据自变量的取值范围来定,并且学习因子分为个体和群体两种;
空间维数:粒子搜索的空间维数即为自变量的个数。
位置限制:限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
速度限制:如果粒子飞行速度过快,很可能直接飞过最优解位置,但是如果飞行速度过慢,会使得收敛速度变慢,因此设置合理的速度限制就很有必要了。
位置限制:限制粒子搜索的空间,即自变量的取值范围,对于无约束问题此处可以省略。
速度限制:如果粒子飞行速度过快,很可能直接飞过最优解位置,但是如果飞行速度过慢,会使得收敛速度变慢,因此设置合理的速度限制就很有必要了。
不同于遗传算法,粒子群算法不需要编码,直接利用粒子的位置来表示自变量,每个粒子的位置都由自变量的个数和取值范围决定,而速度由自变量的个数和速度限制决定,形式如下,其中d代表空间维数(自变量数):
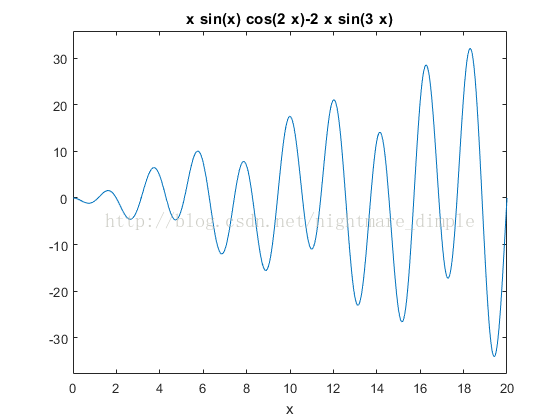
下面我们用一个例子来帮助理解,对于函数 f=x*sin(x)*cos(2*x)-2*x*sin(3*x) ,求其在区间[0,20]上该函数的最大值。首先我们需要画出函数的图像,如下图:
- 初始化种群
位置和速度的初始化即在位置和速度限制内随机生成一个N x d 的矩阵,对于此题,位置初始化也就是在0~20内随机生成一个50x1的数据矩阵,而对于速度则不用考虑约束,一般直接在0~1内随机生成一个50x1的数据矩阵。
此处的位置约束也可以理解为位置限制,而速度限制是保证粒子步长不超限制的,一般设置速度限制为[-1,1]。
粒子群的另一个特点就是记录每个个体的历史最优和种群的历史最优,因此而二者对应的最优位置和最优值也需要初始化。其中每个个体的历史最优位置可以先初始化为当前位置,而种群的历史最优位置则可初始化为原点。对于最优值,如果求最大值则初始化为负无穷,相反地初始化为正无穷。
每次搜寻都需要将当前的适应度和最优解同历史的记录值进行对比,如果超过历史最优值,则更新个体和种群的历史最优位置和最优解。
每次搜寻都需要将当前的适应度和最优解同历史的记录值进行对比,如果超过历史最优值,则更新个体和种群的历史最优位置和最优解。
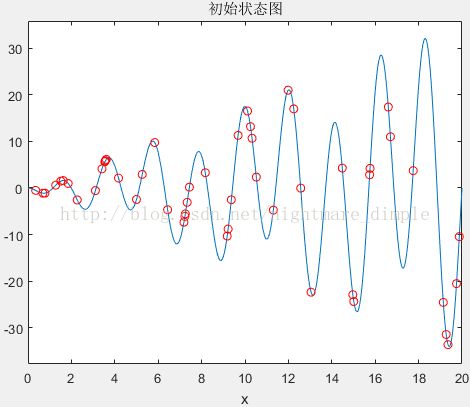
通过之前的参数设定可以得到如下的初始分布图:
- 速度与位置的更新
每次更新完速度和位置都需要考虑速度和位置的限制,需要将其限制在规定范围内,此处仅举出一个常规方法,即将超约束的数据约束到边界(当位置或者速度超出初始化限制时,将其拉回靠近的边界处)。当然,你不用担心他会停住不动,因为每个粒子还有惯性和其他两个参数的影响。
代码如下:
clc;clear;close all;
%% 初始化种群
f= @(x)x .* sin(x) .* cos(2 * x) - 2 * x .* sin(3 * x); % 函数表达式
figure(1);ezplot(f,[0,0.01,20]);
N = 50; % 初始种群个数
d = 1; % 空间维数
ger = 100; % 最大迭代次数
limit = [0, 20]; % 设置位置参数限制
vlimit = [-1, 1]; % 设置速度限制
w = 0.8; % 惯性权重
c1 = 0.5; % 自我学习因子
c2 = 0.5; % 群体学习因子
for i = 1:d
x = limit(i, 1) + (limit(i, 2) - limit(i, 1)) * rand(N, d);%初始种群的位置
end
v = rand(N, d); % 初始种群的速度
xm = x; % 每个个体的历史最佳位置
ym = zeros(1, d); % 种群的历史最佳位置
fxm = zeros(N, 1); % 每个个体的历史最佳适应度
fym = -inf; % 种群历史最佳适应度
hold on
plot(xm, f(xm), 'ro');title('初始状态图');
figure(2)
%% 群体更新
iter = 1;
record = zeros(ger, 1); % 记录器
while iter <= ger
fx = f(x) ; % 个体当前适应度
for i = 1:N
if fxm(i) < fx(i)
fxm(i) = fx(i); % 更新个体历史最佳适应度
xm(i,:) = x(i,:); % 更新个体历史最佳位置
end
end
if fym < max(fxm)
[fym, nmax] = max(fxm); % 更新群体历史最佳适应度
ym = xm(nmax, :); % 更新群体历史最佳位置
end
v = v * w + c1 * rand * (xm - x) + c2 * rand * (repmat(ym, N, 1) - x);% 速度更新
% 边界速度处理
v(v > vlimit(2)) = vlimit(2);
v(v < vlimit(1)) = vlimit(1);
x = x + v;% 位置更新
% 边界位置处理
x(x > limit(2)) = limit(2);
x(x < limit(1)) = limit(1);
record(iter) = fym;%最大值记录
% x0 = 0 : 0.01 : 20;
% plot(x0, f(x0), 'b-', x, f(x), 'ro');title('状态位置变化')
% pause(0.1)
iter = iter+1;
end
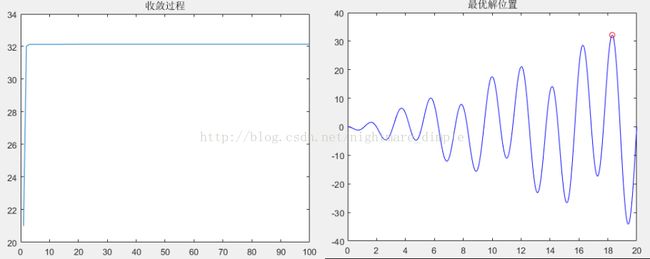
figure(3);plot(record);title('收敛过程')
x0 = 0 : 0.01 : 20;
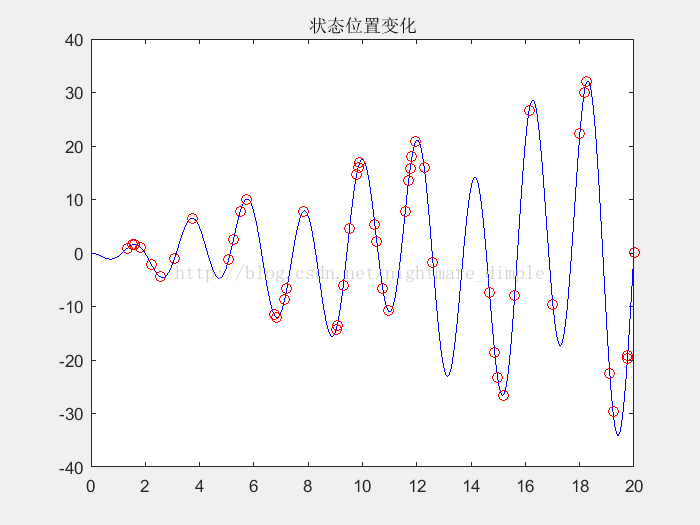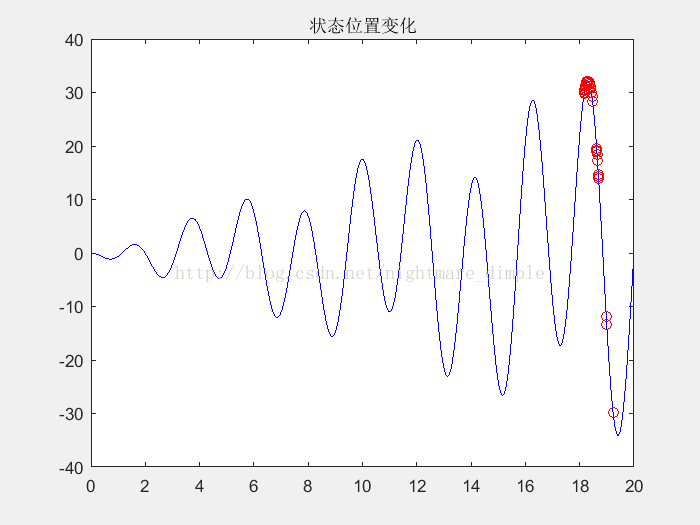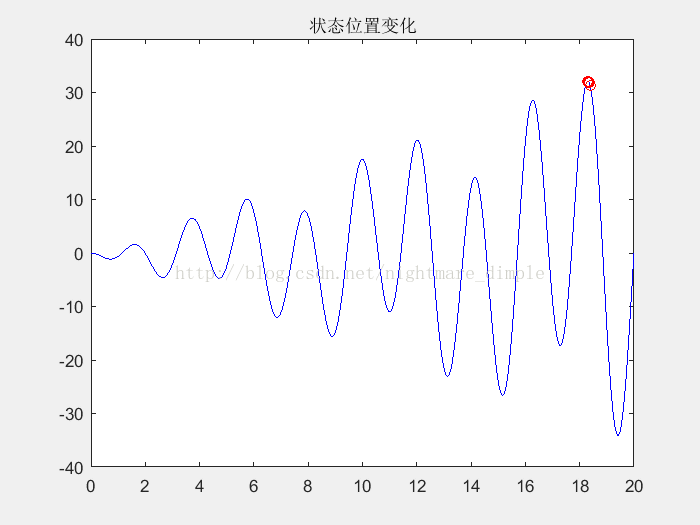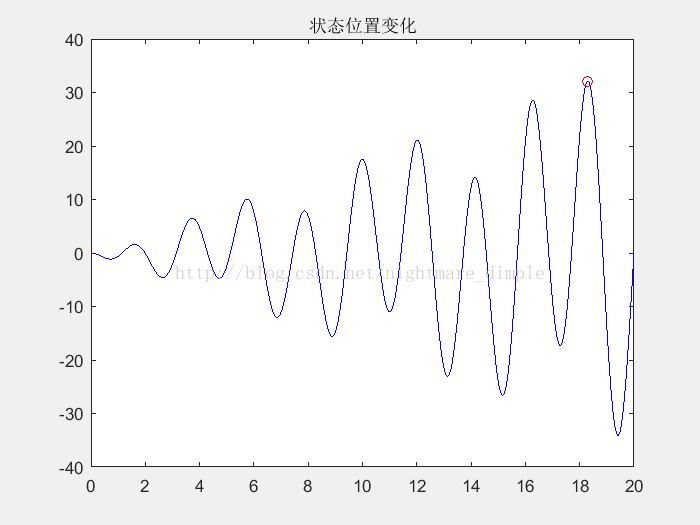
figure(4);plot(x0, f(x0), 'b-', x, f(x), 'ro');title('最终状态位置')
disp(['最大值:',num2str(fym)]);
disp(['变量取值:',num2str(ym)]);
由上图可以看出算法已成功找出了最优解,其最优解为18.3014,而其最大值为32.1462。
如果想看粒子群算法中粒子的搜索过程的可以将代码中注释掉的三行代码放上去。效果是这样的: