线性代数第二章矩阵及其运算
$1.矩阵
定义1
由 m ∗ n 个 数 a i j ( i = 1 , 2 , 3... , n ) 排 成 的 m 行 n 列 的 数 表 由m*n个数a_{ij}(i=1,2,3...,n)排成的m行n列的数表 由m∗n个数aij(i=1,2,3...,n)排成的m行n列的数表
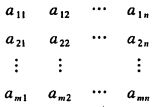
称为m行n列矩阵,简称mn矩阵。为表示它是一个整体,总是加一个括弧,并用大写黑体字母表示,记作

这mn个数称为矩阵A的元素,简称为元,数 a i j a{ij} aij位于矩阵A的第i行第j列,称为矩阵A的(i,j)元。以数 a i , j 元 的 矩 阵 可 简 记 作 ( a i j ) 或 ( a i j ) m ∗ n . m ∗ n 矩 阵 A 也 记 作 A m ∗ n a_{i,j}元的矩阵可简记作(a_{ij})或(a_{ij})m*n. m*n矩阵A也记作A_{m*n} ai,j元的矩阵可简记作(aij)或(aij)m∗n.m∗n矩阵A也记作Am∗n.
元素是实数的矩阵称为实矩阵,元素是复数的矩阵称为复矩阵,本书中的矩阵除特别说明者外,都指实矩阵。
行数与列数都等于n的矩阵称为n阶矩阵或n阶方阵。n阶矩阵A也记作An。
只有一行的矩阵
A = ( a 1 , a 2 , . . . , a n ) A=(a_1,a_2,...,a_n) A=(a1,a2,...,an).
只有一列的矩阵

称为列矩阵,又称列向量。
两个矩阵的行数相等、列数也相等时,就称它们是同型矩阵。如果 A = ( a i j ) 与 B = ( b i j ) 是 同 型 矩 阵 , 并 且 它 们 的 对 应 元 素 相 等 , 即 A=(a_{ij})与B=(b_{ij})是同型矩阵,并且它们的对应元素相等,即 A=(aij)与B=(bij)是同型矩阵,并且它们的对应元素相等,即
![]()
那么就称矩阵A与矩阵B相等,记作
A=B
元素都为零的矩阵称为零矩阵,记作O。注意不同型的零矩阵是不同的。
矩阵的应用非常广泛,下面仅举几例。
例1
某工厂三个商店发送四种产品的数量可列成矩阵

其中 a i j 为 工 厂 向 第 i 店 发 送 第 j 种 产 品 的 数 量 。 a_{ij}为工厂向第i店发送第j种产品的数量。 aij为工厂向第i店发送第j种产品的数量。
这四种产品的单价及单件重量也可列成矩阵
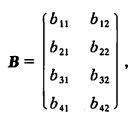
其中 b i 1 为 第 i 种 产 品 的 单 价 , b i 2 为 第 i 种 产 品 的 单 件 重 量 b_{i1}为第i种产品的单价,b_{i2}为第i种产品的单件重量 bi1为第i种产品的单价,bi2为第i种产品的单件重量。
例2
四个城市间的单向航线如图2.1所示:

若令
a i j = { 1 , 从 i 市 到 j 市 有 1 条 单 向 航 线 , 0 , 从 i 市 到 j 市 没 有 单 向 航 线 . a_{ij}=\begin{cases} 1,从i市到j市有1条单向航线,\\ 0,从i市到j市没有单向航线. \end{cases} aij={1,从i市到j市有1条单向航线,0,从i市到j市没有单向航线.
则图2.1可用矩阵表示为

一般的,若干个点之间的单向通道都可以用这样的矩阵表示。
例3
n 个 变 量 x 1 , x 2 , . . . , x n 与 m 个 变 量 y 1 , y 2 , . . . , y m 之 间 的 关 系 式 n个变量x_1,x_2,...,x_n与m个变量y_1,y_2,...,y_m之间的关系式 n个变量x1,x2,...,xn与m个变量y1,y2,...,ym之间的关系式

表示一个从变量 x 1 , x 2 , . . . , x n 到 变 量 y 1 , y 2 , . . . , y m 的 线 性 变 换 , 其 中 a i j 为 常 数 。 线 性 变 换 ( 2 ) 的 系 数 a i j 构 成 矩 阵 A = ( a i j ) m ∗ n x_1,x_2,...,x_n到变量y_1,y_2,...,y_m的线性变换,其中a_{ij}为常数。线性变换(2)的系数a_{ij}构成矩阵A=(a_{ij})_{m*n} x1,x2,...,xn到变量y1,y2,...,ym的线性变换,其中aij为常数。线性变换(2)的系数aij构成矩阵A=(aij)m∗n
给定了线性变换(2),它的系数所构成的矩阵(称为系数矩阵)也就确定。反之,如果给出一个矩阵作为线性变换的系数矩阵,则线性变换也就确定。在这个意义上,线性变换和矩阵之间存在着一一对应的关系。
例如线性变换

叫做恒等变换,它对应的一个n阶方阵

叫做n阶单位矩阵,简称单位阵。这个方阵的特点是:从左上角到右下角的直线(叫做(主)对角线上的元素都是1,其他元素都是0.即单位阵E的(i,j)元为)

又如线性变换
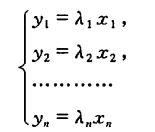
对应n阶方阵

这个方阵的特点是:不在对角线上的元素都是0.这种方阵为对角矩阵,简称对角阵。对角阵也记作
![]()
由于矩阵和线性变换之间存在一一对应的关系,因此可以利用矩阵来研究线性变换,也可以利用线性变换来解释矩阵的含义。
例如矩阵
( 1 0 0 0 ) \begin{pmatrix} 1 & 0 \\ 0 & 0 \end{pmatrix}\quad (1000)
所对应的线性变换
{ x 1 = x , y 1 = 0 \begin{cases} x_1=x, \\ y_1=0 \end{cases} {x1=x,y1=0
可看作是xOy平面上把向量OP= ( x 1 y 1 ) = ( x 0 ) \begin{pmatrix}x_1 \\ y_1 \end{pmatrix}=\begin{pmatrix}x \\ 0 \end{pmatrix} (x1y1)=(x0)的变换(或看作把点P变为点P1的变换,参看图2.2),由于向量OP1是向量OP在x轴上的投影向量(即点P1是点P在x轴上的投影),因此这是一个投影变换。


$2.矩阵的运算
一、矩阵的加法
定义2 设 有 两 个 m ∗ n 矩 阵 A = ( a i j ) 和 B = b i j , 那 么 矩 阵 A 和 B 的 和 记 作 A + B , 规 定 为 设有两个m*n矩阵A=(a_{ij})和B={b_{ij}},那么矩阵A和B的和记作A+B,规定为 设有两个m∗n矩阵A=(aij)和B=bij,那么矩阵A和B的和记作A+B,规定为

应该注意,只有当两个矩阵是同型矩阵时,这两个矩阵才能进行加法运算。
矩阵加法满足下列运算规律(设A,B,C都是m*n矩阵)
( 1 ) A + B = B + A (1)A+B=B+A (1)A+B=B+A
( 2 ) ( A + B ) + C = A + ( B + C ) (2)(A+B)+C=A+(B+C) (2)(A+B)+C=A+(B+C).
设 矩 阵 A = ( a i j ) , 记 设矩阵A=(a_{ij}),记 设矩阵A=(aij),记
− A = ( − a i j ) -A=(-a_{ij}) −A=(−aij)
-A称为矩阵A的负矩阵,显然有
A+(-A)=O,
由此规定矩阵的减法为
A-B=A+(-B).
二、数与矩阵相乘
定义3 数 λ 与 矩 阵 A 的 乘 积 记 作 λ A 或 A λ , 规 定 为 数\lambda 与矩阵A的乘积记作\lambda A或A \lambda,规定为 数λ与矩阵A的乘积记作λA或Aλ,规定为
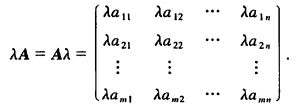
数 乘 矩 阵 满 足 下 列 运 算 规 律 ( 设 A , B 为 m ∗ n 矩 阵 , λ , μ 为 数 ) : 数乘矩阵满足下列运算规律(设A,B为m*n矩阵,\lambda,\mu 为数): 数乘矩阵满足下列运算规律(设A,B为m∗n矩阵,λ,μ为数):
( 1 ) ( λ μ ) A = λ ( μ A ) ; (1)(\lambda \mu)A=\lambda(\mu A); (1)(λμ)A=λ(μA);
( 2 ) ( λ + μ ) A = λ A + μ A ; (2)(\lambda+\mu)A=\lambda A+\mu A; (2)(λ+μ)A=λA+μA;
( 3 ) λ ( A + B ) = λ A + λ B . (3)\lambda(A+B)=\lambda A+\lambda B. (3)λ(A+B)=λA+λB.
矩阵相加与数乘矩阵结合起来,统称为矩阵的线性运算。
三、矩阵与矩阵相乘
设有两个线性变换
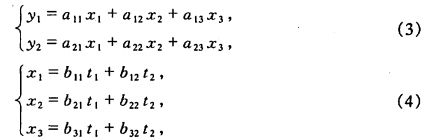
若想求出从 t 1 , t 2 到 y 1 , y 2 的 线 性 变 换 , 可 将 ( 4 ) 代 入 ( 3 ) , 便 得 t_1,t_2到y_1,y_2的线性变换,可将(4)代入(3),便得 t1,t2到y1,y2的线性变换,可将(4)代入(3),便得
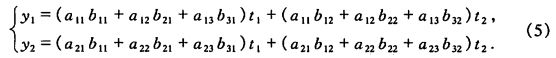
线性变换(5)可看作是先作线性变换(4)再作线性变换(3)的结果。我们把线性变换(5)叫做线性变换(3)与(4)的乘积,相应的把(5)所对应的矩阵定义为(3)与(4)所对应的的矩阵的乘积,即
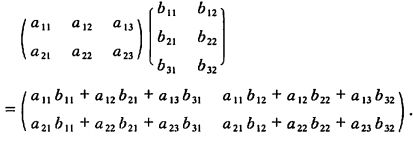
一般的,我们有
定义4 设 A = ( a i j ) 是 一 个 m ∗ s 矩 阵 , B = ( b i j ) 是 一 个 s ∗ n 矩 阵 , 那 么 规 定 矩 阵 A 与 矩 阵 B 的 乘 积 是 一 个 m ∗ n 矩 阵 C = ( c i j ) , 其 中 设A=(a_{ij})是一个m*s矩阵,B=(b_{ij})是一个s*n矩阵,那么规定矩阵A与矩阵B的乘积是一个m*n矩阵C=(c_{ij}),其中 设A=(aij)是一个m∗s矩阵,B=(bij)是一个s∗n矩阵,那么规定矩阵A与矩阵B的乘积是一个m∗n矩阵C=(cij),其中
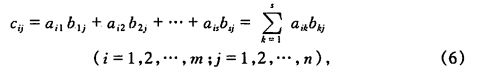
并把此乘积记作
C=AB.
按此定义,一个1s行矩阵与一个s1列矩阵的乘积是一个1阶方阵,也就是一个数。
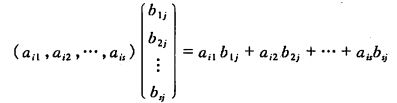
= ∑ k = 1 t a i k b k j = c i j \sum^t_{k=1}a_{ik}b_{kj}=c_{ij} ∑k=1taikbkj=cij,
由此表明乘积矩阵AB=C的(i,j)元cij就是A的第i行与B的第j列的乘积。
必须注意:只有当第一个矩阵(左矩阵)的列数等于第二个矩阵(右矩阵)的行数时,两个矩阵才能相乘。
例4
求矩阵

的乘积AB
解 因为A是24矩阵,B是43矩阵,A的列数等于B的行数,所以矩阵A与B可以相乘,其乘积AB=C是一个2*3矩阵。按公式(6)有
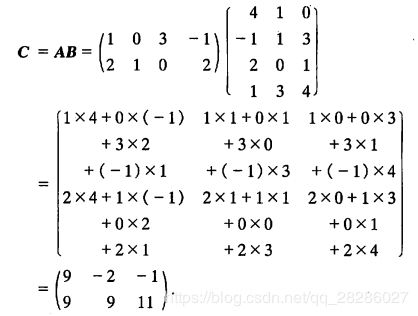
例5
求矩阵

的乘积AB及BA。
解 按公式(6)有
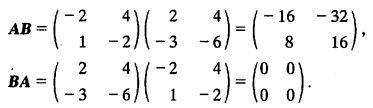
在例4中,A是24矩阵,B是43矩阵,乘积AB有意义而BA却没有意义。由此可知:
1.在矩阵的乘法中必须注意矩阵相乘的顺序
AB是A左乘B(B被A左乘)的乘积,BA是A右乘B的乘积,AB有意义时,BA可以没有意义。
2.若A是mn矩阵,B是nm矩阵,则AB与BA都有意义,但AB是m阶方阵,BA是n阶方阵,当 m ≠ n 时 , A B ≠ B A . 即 使 m = n , 即 A , B 是 同 阶 方 阵 , m\not=n时,AB\not=BA.即使m=n,即A,B是同阶方阵, m=n时,AB=BA.即使m=n,即A,B是同阶方阵,如例5,A与B都是2阶方阵,从而AB与BA也都是2阶方阵,但AB与BA仍然可以不相等。总之,矩阵的乘法不满足交换律,即在一般情形下, A B ≠ B A AB\not=BA AB=BA.
对于两个n阶方阵A,B,若AB=BA,则称方阵A与B是可交换的。
例5还表明
1.矩阵A ≠ O , B ≠ O , 但 却 有 B A = O 。 \not=O,B\not=O,但却有BA=O。 =O,B=O,但却有BA=O。这就提醒读者要特别注意:若有两个矩阵A,B满足AB=O,不能得出A=O或B=O的结论;
2.若 A ≠ O 而 A ( X − Y ) = O , 也 不 能 得 出 X = Y 的 结 论 。 A\not=O而A(X-Y)=O,也不能得出X=Y的结论。 A=O而A(X−Y)=O,也不能得出X=Y的结论。
矩阵的乘法虽不满足交换律,但仍满足下列结合律和分配率(假设运算都是可行的):

对于单位矩阵E,容易验证
![]()
可见单位矩阵E在矩阵乘法中的作用类似于数1.
矩阵

称为纯量阵。由 ( λ E ) A = λ A , A ( λ E ) = λ A , (\lambda E)A=\lambda A,A(\lambda E)=\lambda A, (λE)A=λA,A(λE)=λA,可知纯量阵 λ E 与 矩 阵 A 的 乘 积 等 于 数 λ 与 A 的 乘 积 。 \lambda E与矩阵A的乘积等于数\lambda与A的乘积。 λE与矩阵A的乘积等于数λ与A的乘积。并且当A为n阶方阵时,有
( λ E n ) A n = λ A n = A n ( λ E n ) , (\lambda E_n)A_n=\lambda A_n=A_n(\lambda E_n), (λEn)An=λAn=An(λEn),
表明纯量阵 λ E \lambda E λE与任何同阶方阵都是可交换的。
有了矩阵的乘法,就可以定义矩阵的幂。设A是n阶方阵,定义
A 1 = A , A 2 = A 1 ∗ A 1 , . . . , A k + 1 = A k A 1 , A^1=A,A^2=A^1*A^1,...,A^{k+1}=A^kA^1, A1=A,A2=A1∗A1,...,Ak+1=AkA1,
其中k为正整数,这就是说 A k 就 是 k 个 A 连 乘 。 显 然 只 有 方 阵 , 它 的 幂 才 有 意 义 。 A^k就是k个A连乘。显然只有方阵,它的幂才有意义。 Ak就是k个A连乘。显然只有方阵,它的幂才有意义。
由于矩阵乘法适合结合律,所以矩阵的幂满足以下运算规律:
A k A l = A k + l , ( A k ) l = A k l , A^kA^l=A^{k+l},(A^k)^l=A^{kl}, AkAl=Ak+l,(Ak)l=Akl,
其中k,l为正整数,又因矩阵乘法一般不满足交换律,所以对于两个n阶矩阵A与B,一般说来 ( A B ) k ≠ A k B k , 只 有 当 A 与 B 可 交 换 时 , 才 有 ( A B ) k = A k B k . (AB)^k\not=A^kB^k,只有当A与B可交换时,才有(AB)^k=A^kB^k. (AB)k=AkBk,只有当A与B可交换时,才有(AB)k=AkBk.
类似可知,例如 ( A + B ) 2 = A 2 + 2 A B + B 2 , ( A − B ) ( A + B ) = A 2 − B 2 (A+B)^2=A^2+2AB+B^2,(A-B)(A+B)=A^2-B^2 (A+B)2=A2+2AB+B2,(A−B)(A+B)=A2−B2等公式,也只有当A与B可交换时才成立。
上节例1中有一个向三个商店发送四种产品的数量所构成的矩阵A、一个四种产品的单价与单价重量所构成的矩阵B,按矩阵相乘的定义,可知A与B的乘积矩阵AB=C= ( c i j ) 3 ∗ 2 (c_{ij})_{3*2} (cij)3∗2为三个商店所发产品的总值及总重量所构成的矩阵,即 c i 1 为 向 第 i 店 所 发 产 品 的 总 值 , c i 2 c_{i1}为向第i店所发产品的总值,c_{i2} ci1为向第i店所发产品的总值,ci2为向第i店所发产品的总重量。
上节例2中有一个四城市间的单向航线矩阵A,由

记 A 2 = ( b i j ) , 则 b i j 为 从 i 市 一 次 中 转 到 j 市 的 单 向 航 线 条 数 。 A^2=(b_{ij}),则b_{ij}为从i市一次中转到j市的单向航线条数。 A2=(bij),则bij为从i市一次中转到j市的单向航线条数。
例如
b 23 = 1 b_{23}=1 b23=1,显示从2市经一次中转到3市的单向航线有1条(2-1-3,参看图2.1);
b 42 = 2 b_{42}=2 b42=2,显示从4市经一次中转到2市的单向航线有2条(4-1-2,4-3-2);
b 11 = 2 b_{11}=2 b11=2,显示过1市的双向航线有2条(1-2-1,1-4-1);
b 33 = 0 b_{33}=0 b33=0,显示3市没有双向航线。
上节例3中的线性变换
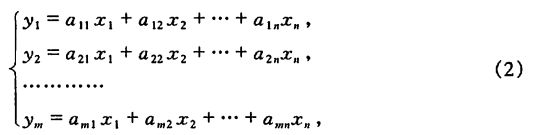
利用矩阵的乘法,可记作
Y+AX,
其中

这里,列向量(列矩阵)X表示n个变量 x 1 , x 2 , . . . , x n , 列 向 量 Y x_1,x_2,...,x_n,列向量Y x1,x2,...,xn,列向量Y表示m个
变量 y 1 , y 2 , . . . , y n y_1,y_2,...,y_n y1,y2,...,yn.线性变换(2)把X变成Y,相当于用矩阵A去左乘X得到Y。
用矩阵A= ( 1 0 0 0 ) \begin{pmatrix} 1 & 0 \\ 0&0 \end{pmatrix} (1000)去左乘向量OP= ( x y ) \begin{pmatrix} x\\ y \end{pmatrix} (xy),相当于把向量OP投影到X轴上。(参看图2.2)

例6
四、矩阵的转置
定义5 把矩阵A的行换成同序数的列得到一个新矩阵,叫做A的转置矩阵,记作 A T A^T AT。例如矩阵

矩阵转置也是一种运算,满足下述运算规律(假设运算都是可行的):
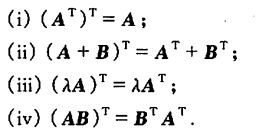
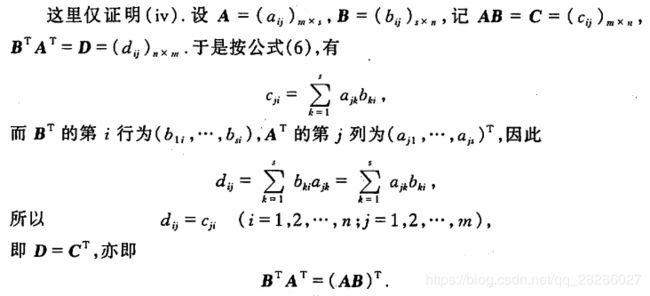
例7
已知

求 ( A B ) T (AB)^T (AB)T.
解法1

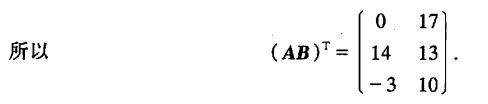
解法2

设A为n阶方阵,如果满足 A T = A , A^T=A, AT=A,即
![]()
那么A称为对称矩阵,简称对称阵。对称阵的特点是:它的元素以对角线为对称轴对应相等。
例8
设 列 矩 阵 X = ( x 1 , x 2 , . . . , x n ) T 满 足 X T X = 1 , E 为 n 阶 单 位 阵 , H = E − 2 X X T , 证 明 X X T 设列矩阵X=(x_1,x_2,...,x_n)^T满足X^TX=1,E为n阶单位阵,H=E-2XX^T,证明XX^T 设列矩阵X=(x1,x2,...,xn)T满足XTX=1,E为n阶单位阵,H=E−2XXT,证明XXT是n阶方阵。
证明前先提醒读者注意: X T X = x 1 2 + x 2 2 + . . . + x n 2 X^TX=x_1^2+x_2^2+...+x_n^2 XTX=x12+x22+...+xn2是一阶方阵,也就是一个数,而 X X T 是 n 阶 方 阵 。 XX^T是n阶方阵。 XXT是n阶方阵。

五、方阵的行列式
定义6 由n阶方阵A的元素所构成的行列式(各元素的位置不变),称为方阵A的行列式,记作|A|或detA
应该注意,方阵与行列式是两个不同的概念,n阶方阵是 n 2 n^2 n2个数按一定方式排成的数表,而n阶行列式则是这些数(也就是数表A)按一定的运算法则所确定的一个数。
由A确定|A|的这个运算满足下述运算规律(设A,B为n阶方阵, λ \lambda λ为数):

我们仅证明(iii). 设 A = ( a i j ) , B = ( b i j ) . 记 2 n 阶 行 列 式 设A=(a_{ij}),B=(b_{ij}).记2n阶行列式 设A=(aij),B=(bij).记2n阶行列式

由第一章例10可知 D = ∣ A ∣ ∣ B ∣ , 而 在 D 中 以 b 1 j 乘 以 第 1 列 , b 2 j 乘 以 第 2 列 . . . , b n j 乘 第 n 列 , 都 加 到 第 n + j 列 上 ( j = 1 , 2.. , n ) D=|A||B|,而在D中以b_{1j}乘以第1列,b_{2j}乘以第2列...,b_{nj}乘第n列,都加到第n+j列上(j=1,2..,n) D=∣A∣∣B∣,而在D中以b1j乘以第1列,b2j乘以第2列...,bnj乘第n列,都加到第n+j列上(j=1,2..,n),有

其中
![]()
故 C=AB
再对D的行作
![]()
有
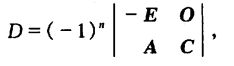
从而按第一章例10有
![]()
于是
![]()
由(iii)可知,对于n阶矩阵A,B,一般来说 A B ≠ B A , 但 总 有 AB\not=BA,但总有 AB=BA,但总有
∣ A B ∣ = ∣ A B ∣ ⋅ ∣ B A ∣ |AB|=|AB|\cdot|BA| ∣AB∣=∣AB∣⋅∣BA∣
例9
行列式|A|的各个元素的代数余子式 A i j 所 构 成 的 如 下 的 矩 阵 A_{ij}所构成的如下的矩阵 Aij所构成的如下的矩阵

称为矩阵A的伴随矩阵,简称伴随阵,试证

六、共轭矩阵
$3.逆矩阵
设给定一个线性变换
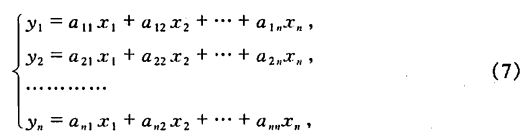
它的系数矩阵是一个n阶矩阵A,若记

则线性变换(7)可记作
Y=AX. (8)
以A的伴随阵A*左乘上式两端,并利用例9的结果,可得
![]()
当 ∣ A ∣ ≠ 0 时 , 可 解 出 当|A| \not= 0时,可解出 当∣A∣=0时,可解出
![]()
记 B = 1 ∣ A ∣ A ∗ 记B=\frac{1}{|A|}A* 记B=∣A∣1A∗,上式可记作
![]()
(9)式表示一个从Y到X的线性变换,称为线性变换(8)的逆变换。
我们从(8)(9)两式分析变换所对应的方阵A与逆变换所对应的方阵B之间的关系。用(9)代入(8),可得
Y=A(BY)=(AB)Y.
可见AB为恒等变换所对应的矩阵,故AB=E。用(8)式代入(9)得
X=B(AX)=(BA)X.
因此,BA=E,于是有
AB=BA=E。
由此我么引入逆矩阵的定义。
定义7 对于n阶矩阵A,如果有一个n阶矩阵B,使
AB=BA=E,
则说矩阵A是可逆的,并把矩阵B称为A的逆矩阵,简称逆阵。
如果矩阵A是可逆的,那么A的逆阵是唯一的。这是因为:设B,C都是A的逆阵,则有
B=BE=B(AC)=(BA)C=EC=C,
所以A的逆阵是惟一的。
A的逆阵记作 A − 1 A^{-1} A−1,即若AB=BA=E,则B= A − 1 A^{-1} A−1.
定理1 若矩阵A可逆,则|A| ≠ 0 \not= 0 =0.
证
A 可 逆 , 即 有 A − 1 , 使 A A − 1 = E . 故 ∣ A ∣ . ∣ A − 1 ∣ = ∣ E ∣ = 1 , 所 以 ∣ A ∣ ≠ 0. A可逆,即有A^-1,使AA^-1=E.故|A|.|A^-1|=|E|=1,所以|A|\not=0. A可逆,即有A−1,使AA−1=E.故∣A∣.∣A−1∣=∣E∣=1,所以∣A∣=0.
定理2 若 ∣ A ∣ ≠ 0 , 则 矩 阵 A 可 逆 , 且 |A|\not=0,则矩阵A可逆,且 ∣A∣=0,则矩阵A可逆,且

其中A为矩阵A的伴随阵。
证:
由例9知
AA=A*A=|A|E,
因 ∣ A ∣ ≠ 0 , 故 有 因|A|\not=0,故有 因∣A∣=0,故有
A 1 ∣ A ∣ A ∗ = 1 ∣ A ∣ A ∗ A = E , A\frac{1}{|A|}A^*=\frac{1}{|A|}A^*A=E, A∣A∣1A∗=∣A∣1A∗A=E,
所以,按逆阵的定义,即知A可逆,且有
A − 1 = 1 ∣ A ∣ A ∗ A^-1=\frac{1}{|A|}A^* A−1=∣A∣1A∗
当|A|=0时,A称为奇异矩阵,否则称为非奇异矩阵。由上面两定理可知:A是可逆矩阵的充分必要条件是|A|不等于0,即可逆矩阵就是非奇异矩阵。
由定理2,可得下述推论
![]()
证
∣ A ∣ ∗ ∣ B ∣ = ∣ E ∣ = 1 , 故 ∣ A ∣ ≠ 0 , 因 而 A − 1 存 在 , 于 是 |A|*|B|=|E|=1,故|A|\not=0,因而A^-1存在,于是 ∣A∣∗∣B∣=∣E∣=1,故∣A∣=0,因而A−1存在,于是
B = E B = ( A − 1 A ) B = A − 1 ( A B ) = A − 1 E = A − 1. B=EB=(A^-1A)B=A^-1(AB)=A^-1E=A^-1. B=EB=(A−1A)B=A−1(AB)=A−1E=A−1.
方阵的逆满足下述运算规律:

证
( A B ) ( B − 1 A − 1 ) = A ( B B − 1 ) A − 1 = A E A − 1 = E , (AB)(B^{-1}A^{-1})=A(BB^{-1})A^{-1}=AEA^{-1}=E, (AB)(B−1A−1)=A(BB−1)A−1=AEA−1=E,由推论,即有
( A B ) − 1 = B − 1 A − 1 (AB)^{-1}=B^{-1}A^{-1} (AB)−1=B−1A−1
![]()
证
A T ( A − 1 ) T = ( A − 1 A ) T = E T = E , A^T(A^{-1})^T=(A^{-1}A)^T=E^T=E, AT(A−1)T=(A−1A)T=ET=E,
所以
![]()
当A可逆时,还可定义

例10
求二阶矩阵A=
( a b c d ) 的 逆 阵 \begin{pmatrix} a & b \\ c &d\end{pmatrix}的逆阵 (acbd)的逆阵
解:
∣ A ∣ = a d − b c , A ∗ = ( d − b − c a ) |A|=ad-bc,A^*=\begin{pmatrix} d & -b \\ -c &a\end{pmatrix} ∣A∣=ad−bc,A∗=(d−c−ba),
利用逆阵公式(10),当|A|不等于0时,有
A − 1 = 1 ∣ A ∣ A ∗ = 1 a d − b c ( d − b − c a ) A^{-1}=\frac{1}{|A|}A^*=\frac{1}{ad-bc}\begin{pmatrix} d & -b \\ -c &a\end{pmatrix} A−1=∣A∣1A∗=ad−bc1(d−c−ba)
例11
例12
设

求矩阵X使其满足
AXB=C
解
若 A − 1 , B − 1 存 在 , 则 用 A − 1 左 乘 上 式 , B − 1 右 乘 上 式 , 有 若A^{-1},B^{-1}存在,则用A^{-1}左乘上式,B^{-1}右乘上式,有 若A−1,B−1存在,则用A−1左乘上式,B−1右乘上式,有
A − 1 A X B B − 1 = A − 1 C B − 1 A^{-1}AXBB^{-1}=A^{-1}CB^{-1} A−1AXBB−1=A−1CB−1,
即
X = A − 1 C B − 1 X=A^{-1}CB^{-1} X=A−1CB−1
由上例知|A|不等于0,而|B|=1,故知A,B都可逆,且
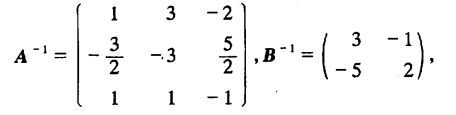

例13
设 P = ( 1 2 1 4 ) , Λ = ( 1 0 0 2 ) , A P = P Λ , 求 A n P=\begin{pmatrix} 1&2 \\1&4 \end{pmatrix},Λ=\begin{pmatrix} 1&0 \\0&2 \end{pmatrix},AP=PΛ,求A^n P=(1124),Λ=(1002),AP=PΛ,求An.
解
A = P Λ P − 1 , A 2 = P Λ P − 1 P Λ P − 1 = P Λ 2 P − 1 , A n = P Λ n P − 1 , A=PΛP^{-1},A^2=PΛP^{-1}PΛP^{-1}=PΛ^2P^{-1,A^n=PΛ^nP^{-1}}, A=PΛP−1,A2=PΛP−1PΛP−1=PΛ2P−1,An=PΛnP−1,
而
Λ = ( 1 0 0 2 ) , Λ 2 = ( 1 0 0 2 ) ( 1 0 0 2 ) = ( 1 0 0 2 2 ) , A n = ( 1 0 0 2 n ) , Λ=\begin{pmatrix} 1&0 \\0&2 \end{pmatrix},Λ^2=\begin{pmatrix} 1&0 \\0&2 \end{pmatrix}\begin{pmatrix} 1&0 \\0&2 \end{pmatrix}=\begin{pmatrix} 1&0 \\0&2^2 \end{pmatrix},A^n=\begin{pmatrix} 1&0 \\0&2^n \end{pmatrix}, Λ=(1002),Λ2=(1002)(1002)=(10022),An=(1002n),
∣ P ∣ = 2 , P − 1 = 1 2 ( 4 − 2 − 1 1 ) |P|=2,P^{-1}=\frac{1}{2}\begin{pmatrix} 4&-2 \\-1&1 \end{pmatrix} ∣P∣=2,P−1=21(4−1−21)
故 A n = ( 1 2 1 4 ) ( 1 0 0 2 n ) 1 2 ( 4 − 2 − 1 1 ) = 故A^n=\begin{pmatrix} 1&2 \\1&4 \end{pmatrix}\begin{pmatrix} 1&0 \\0&2^n \end{pmatrix}\frac{1}{2}\begin{pmatrix} 4&-2 \\-1&1 \end{pmatrix}= 故An=(1124)(1002n)21(4−1−21)=
1 2 ( 1 2 n + 1 1 2 n + 2 ) ( 4 − 2 − 1 1 ) = 1 2 ( 4 − 2 n + 1 2 n − 1 2 − 2 n + 1 2 n + 1 − 1 ) \frac{1}{2}\begin{pmatrix} 1&2^{n+1} \\1&2^{n+2} \end{pmatrix}\begin{pmatrix} 4&-2 \\-1&1 \end{pmatrix}=\frac{1}{2}\begin{pmatrix} 4-2^{n+1}&2^{n}-1 \\2-2^{n+1}&2^{n+1}-1 \end{pmatrix} 21(112n+12n+2)(4−1−21)=21(4−2n+12−2n+12n−12n+1−1).
设 φ ( x ) = a 0 + a 1 x + . . . + a m x m \varphi(x)=a_{0}+a_{1}x+...+a_{m}x^m φ(x)=a0+a1x+...+amxm
为 x 的 m 次 多 项 式 , A 为 n 阶 矩 阵 , 记 x的m次多项式,A为n阶矩阵,记 x的m次多项式,A为n阶矩阵,记
φ ( A ) = a 0 E + a 1 A + . . . + a m A m \varphi(A)=a_0E+a_{1}A+...+a_{m}A^m φ(A)=a0E+a1A+...+amAm,\varphi(A)称为矩阵A的m次多项式
因为矩阵 A k , A l 和 E 都 是 可 交 换 的 , 所 以 矩 阵 A 的 两 个 多 项 式 φ ( A ) 和 f ( A ) 总 是 可 交 换 的 , 即 总 有 : A^k,A^l和E都是可交换的,所以矩阵A的两个多项式\varphi(A)和f(A)总是可交换的,即总有: Ak,Al和E都是可交换的,所以矩阵A的两个多项式φ(A)和f(A)总是可交换的,即总有:
φ ( A ) f ( A ) = f ( A ) = φ ( A ) , \varphi(A)f(A)=f(A)=\varphi(A), φ(A)f(A)=f(A)=φ(A),
从而A的几个多项式可以像数x的多项式一样相乘或分解因式。例如
( E + A ) ( 2 E − A ) = 2 E + A − A 2 , (E+A)(2E-A)=2E+A-A^2, (E+A)(2E−A)=2E+A−A2,
( E − A ) 3 = E − 3 A + 3 A 2 − A 3 . (E-A)^3=E-3A+3A^2-A^3. (E−A)3=E−3A+3A2−A3.
我们常用例13中计算 A k 的 方 法 来 计 算 A 的 多 项 式 φ ( A ) , 这 就 是 : A^k的方法来计算A的多项式\varphi(A),这就是: Ak的方法来计算A的多项式φ(A),这就是:
( i ) 如 果 A = P Λ P − 1 , 则 A k = P Λ k P − 1 , 从 而 (i)如果A=P\Lambda P^{-1},则A^k=PΛ^kP^{-1},从而 (i)如果A=PΛP−1,则Ak=PΛkP−1,从而
φ ( A ) = a 0 E + a 1 A + . . . + a m A m \varphi(A)=a_0E+a_1A+...+a_mA^m φ(A)=a0E+a1A+...+amAm
= a 0 E A 0 + a 1 A + . . . + a m A m =a_0EA^0+a_1A+...+a_mA^m =a0EA0+a1A+...+amAm
= a 0 E P P − 1 + a 1 P Λ P − 1 + . . . + a m P Λ m P − 1 =a_0EPP^{-1}+a_{1}PΛP^{-1}+...+a_{m}PΛ^mP^{-1} =a0EPP−1+a1PΛP−1+...+amPΛmP−1
= P a 0 E P − 1 + P a 1 Λ P − 1 + . . . + P a m Λ m P − 1 =Pa_0EP^{-1}+Pa_{1}ΛP^{-1}+...+Pa_{m}Λ^mP^{-1} =Pa0EP−1+Pa1ΛP−1+...+PamΛmP−1
= P φ ( Λ ) P − 1 =P\varphi(Λ)P^{-1} =Pφ(Λ)P−1
(ii)如果 Λ = d i a g ( λ 1 , λ 2 , . . . λ n ) 为 对 角 阵 , 则 Λ k = d i a g ( λ 1 k , λ 2 k , λ 3 k , . . . , λ n k ) \Lambda=diag(\lambda_{1},\lambda_{2},...\lambda_{n})为对角阵,则\Lambda^{k}=diag(λ_1^k,λ_2^k,λ_3^k,...,λ_n^k) Λ=diag(λ1,λ2,...λn)为对角阵,则Λk=diag(λ1k,λ2k,λ3k,...,λnk),从而
φ ( Λ ) = a 0 E + a 1 A + . . . + a m A m \varphi(Λ)=a_0E+a_{1}A+...+a_{m}A^m φ(Λ)=a0E+a1A+...+amAm




