欧拉回路/路径浅谈(七桥问题,两种算法)

前言

欧拉回路/路径在编程中经常涉及,而找欧拉回路/路径是出题者经常要考的东西…

引子

欧拉回路、路径问题来源于18世纪著名古典数学问题之一,问题如下：
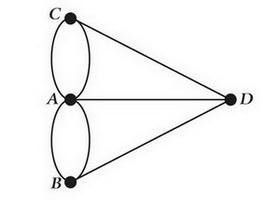
在哥尼斯堡的一个公园里，有七座桥将普雷格尔河中两个岛及岛与河岸连接起来。问是否可能从这四块陆地中任一块出发，恰好通过每座桥一次，再回到起点？

欧拉就凭借这个开创了数学的一个新的分支——图论与几何拓扑，也由此展开了数学史上的新历程。
欧拉发现当地居民有一项消遣活动，就是试图每座桥恰好走过一遍并回到原出发点，但从来没人成功过。
欧拉证明了这种走法是不可能的。现在看来，欧拉的证明过程非常简单，但他对七桥问题的抽象和论证思想，开创了一个新的学科：图论(Graph)。
如今，无论是数学、物理、化学、天文、地理、生物等基础科学，还是信息、交通、经济乃至社会科学的众多问题，都可以应用图论方法予以解决。图论还是计算机科学的数据结构和算法中最重要的框架.
好了，那么这个问题的证明呢?
欧拉DL给出的证明极为简单：
假设每座桥都恰好走过一次，那么对于A、B、C、D四个顶点中的每一个顶点，需要从某条边进入，同时从另一条边离开。进入和离开顶点的次数是相同的，即每个顶点有多少条进入的边，就有多少条出去的边，也就是说，每个顶点相连的边是成对出现的，即每个顶点的相连边的数量必须是偶数。但是原图不成立,所以问题无法达成.

欧拉回路/路径

定义

先给出定义:

欧拉路径

在图上用一种走法经过所有的边一次且只有一次的路径叫做欧拉路径，即一笔画。

欧拉回路

在欧拉路径的基础上,如果这条路径的起点和终点重合，那么就是欧拉回路。
我们有知道,编程中图分为有向图和无向图,那么到底什么时候存在欧拉回路/路径呢？
我们来看看：

无向图(连通)

这里先说回路好理解一些

欧拉回路-无向

也就说明,对于每一个点进入和离开顶点的次数是相同的,但由于是那么对于每个边是无向的,所以对于每个点都是偶点(所连边为偶数)

欧拉路径-无向

这里说明了除了起点和终点外都是偶点,起点终点为奇点

有向图(连通)

仿照上面所说的无向图

欧拉回路-有向

还是对于每一个点进入和离开顶点的次数是相同的,所以对于每个点出度等于入度

欧拉路径-有向

由于起点和终点不同，那么起点的出度显然比它的入度少一，终点的入度显然比它的出度少一,而其他点的入度等于出度

注意事项

虽然我们知道定义中：
$欧拉回路\subset 欧拉路径$
但是对于一个连通图来说,如果它存在欧拉回路,那么它就一定不存在欧拉非回路(说法有点不严谨),相当于回路和非回路是对立的

算法

首先要判断是否有欧拉回路/路径
主要有两种算法,都是找欧拉路径(至于回路上面已经有了解释)
两种算法都要提前找到起点(为欧拉回路时即为任意点),同时还要保证图的连通性

Fluery算法

同DFS，从起点开始,对于每个点都尝试与它所连的边走是否能形成欧拉路径,是一个搜索回溯的过程,时间复杂度为$O(E^2)$

Hierholzer算法

这个算法优于第一个,时间复杂度为$O(V+E)$，这个算法还有一个名字叫作逐步插入回路法。
这算法的核心思想很简单:
在满足欧拉路径性质的子图中,加入一个环仍后可一笔画完成.
而实现就是起点开始,DFS走到它所连接的点时删去这条边,顺着继续操作,结束时在一个栈中放入此时点的编号,最后倒序倒序输出即可。
算法流程图如下:

1.判断有无解,确定起点
2.开始递归函数Hierholzer(x):
　　循环寻找与x相连的边(x,u):
　　　　删除(x,u),删除(u,x)
　　　　Hierholzer(u);
　　将x插入答案栈之中
3.输出答案栈

代码大概长这个样子:

void Hierholzer(int u){
	int siz=G[u].size();
	for(int i=0;i<siz;i++){
		int v=G[u][i].to,id=G[u][i].id;
		if(vis[id]) continue;
		vis[id]=1;
		Hierholzer(v);
	}
	Ans.push(u);
	return ;
}

习题

裸题

传送门
UVA-欧拉回路
首先,你各种判断无解,选起点已经够你搞一阵子了…
由于这道题是输出边,所以递归时还要传这条边的编号
然后,这道题虽然是裸题,但是你应该也会T的…因为你的$Hierholzer$函数不优秀…因为你每次还是要枚举所有该点连接的所有边,就算你只剩一条,你还是要枚举完,当你遇到一个极大的环后就会T掉.于是对于一个点可以用一个Now函数记录一下它下一个访问的点在邻接表中的编号,因为你回来后要遍历此时$[i+1,Now[u]-1]$但是显然是浪费时间的.
然后就可以过了
虽然我写的代码跑出来不快,但是自我感觉思路很清晰(其实Wa了5遍…)
代码中特判都有注释的,了解一下

代码

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define LL long long
using namespace std;
int read(){
    int f=1,x=0;char s=getchar();   
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}  
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
#define MAXN 200000
#define INF 0x3f3f3f3f
struct node{
	int f,to,id;
	node(){}//f表示正向边还是反向边
	node(int F,int T,int I){f=F,to=T,id=I;}
};
stack<int> Ans;
bool vis[MAXN+5];
vector<node> G[MAXN+5];
int Siz[MAXN+5],Now[MAXN+5];
inline void Pr(){puts("NO");exit(0);}
void DFS(int u,int Id){
	for(int i=Now[u];i<Siz[u];i++){
		int v=G[u][i].to,id=G[u][i].id;
		Now[u]++;//访问遍历优化
		if(!vis[id])
			vis[id]=1,DFS(v,id*G[u][i].f);
		i=Now[u]-1;
	}
	if(Id) Ans.push(Id);
	return ;
}
int u[MAXN+5],v[MAXN+5],Ru[MAXN+5],Chu[MAXN+5];
int main(){
	int S=0,t=read(),m=read(),n=read();
	if(n==1){//n为1时特判
		if(read()==read()) printf("YES\n1\n");
		else puts("NO");
		return 0;
	}
	if(t==1){//无向图
		for(int i=1;i<=n;i++){
			u[i]=read(),v[i]=read();
			G[u[i]].push_back(node(1,v[i],i)),G[v[i]].push_back(node(-1,u[i],i));
		}
		for(int i=1;i<=m;i++)
			if(G[i].size()%2)
				Pr();//所连边数为奇数：不存在欧拉回路
	}
	else{//有向图
		for(int i=1;i<=n;i++){
			u[i]=read(),v[i]=read();
			Ru[v[i]]++,Chu[u[i]]++;//计算每个点出度入度
			G[u[i]].push_back(node(1,v[i],i));
		}
		for(int i=1;i<=m;i++)
			if(Chu[i]!=Ru[i])
				Pr();//出度不等于入度:不存在欧拉回路
	}
	for(int i=1;i<=m;i++)
		Siz[i]=G[i].size();
	for(int i=1;i<=m;i++)
		if(Siz[i]){//由于是欧拉回路,起点任意
			S=i;
			break;
		}
	DFS(S,0);
	if(int(Ans.size())!=n)
		Pr();//图不连通
	puts("YES");
	while(!Ans.empty()){//用栈输出答案
		printf("%d",Ans.top()),Ans.pop();
		if(!Ans.empty()) putchar(' ');
		else putchar('\n');
	}
	return 0;
}

欧拉回路/路径隐藏

如果没有欧拉,是不是觉得爆炸了…
其实就是求欧拉路径即可,跟上道题很像,只是有了实际背景需要看出来
觉得代码跟上面的差不多…

代码

#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#define LL long long
using namespace std;
int read(){
    int f=1,x=0;char s=getchar();   
    while(s<'0'||s>'9'){if(s=='-')f=-1;s=getchar();}  
    while(s>='0'&&s<='9'){x=x*10+s-'0';s=getchar();}
    return x*f;
}
#define MAXN 200000
#define INF 0x3f3f3f3f
struct node{
	int f,to,id;
	node(){}
	node(int F,int T,int I){f=F,to=T,id=I;}
};
stack<int> Ans;
bool vis[MAXN+5];
vector<node> G[MAXN+5];
void DFS(int u,int fa){
	int siz=G[u].size();
	for(int i=0;i<siz;i++){
		int v=G[u][i].to,id=G[u][i].id;
		if(vis[id]) continue;
		vis[id]=1;
		DFS(v,id*G[u][i].f);
	}
	if(fa) Ans.push(fa);
	return ;
}
void Pr(){puts("NO");exit(0);}
int Ru[MAXN+5],Chu[MAXN+5];
int U[MAXN+5],V[MAXN+5];
int main(){
	//freopen("merge.in","r",stdin);
	//freopen("merge.out","w",stdout);
	int S=0,T=0;
	int t=read(),m=read(),n=read();
	if(t==1){
		for(int i=1;i<=n;i++){
			U[i]=read(),V[i]=read();
			G[U[i]].push_back(node(1,V[i],i)),G[V[i]].push_back(node(-1,U[i],i));
		}
		for(int i=1;i<=n;i++)
			if(G[i].size()%2){
				if(T) Pr();
				if(S) T=i;
				else S=i;
			}
	}
	else{
		for(int i=1;i<=n;i++){
			U[i]=read(),V[i]=read();
			Ru[V[i]]++,Chu[U[i]]++;
			G[U[i]].push_back(node(1,V[i],i));
		}
		for(int i=1;i<=n;i++){
			if(Chu[i]>Ru[i]){
				if(S) Pr();
				S=i;
			}
			if(Chu[i]<Ru[i]){
				if(T) Pr();
				T=i;
			}
		}
	}
	if(!S&&!T)//欧拉回路
		for(int i=1;i<=n;i++)
			if(G[i].size()){
				if(S) T=i;
				else S=i;
			}
	DFS(S,0);
	puts("YES");
	while(!Ans.empty()){
		printf("%d",Ans.top()),Ans.pop();
		if(!Ans.empty()) putchar(' ');
		else putchar('\n');
	}
	return 0;
}

题外话

有关欧拉回路/路径的题,其实看出来了,写好了判断是否为欧拉回路/路径基本就可以过了…