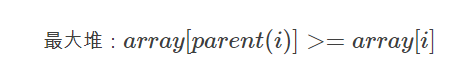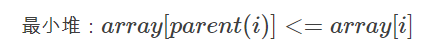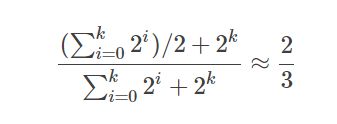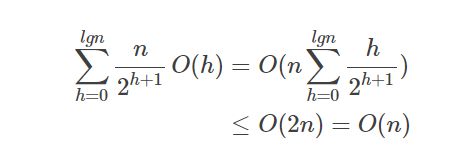二叉堆(Binary Heap)
本文相关代码参见 Algorithms/BinaryHeap
定义
二叉堆本质上是一个数组表示的近似完全的二叉树。数组中的数与二叉树BFS层次遍历一一对应。
[站外图片上传中...(image-511b05-1514818541338)]
上图是截自CLRS的1-index数组和二叉树的对应关系。出于个人编程习惯我们以下都以数组0-index为例(1-index按照下标关系类推即可),根节点存储在数组0下标位置,父节点与对应的左右子节点的下标满足以下关系
//获取父节点下标
inline size_t parent(size_t i){
return (i-1)>>1;
}
//获取左儿子下标
inline size_t left(size_t i){
return (i<<1)+1;
}
//获取右儿子下标
inline size_t right(size_t i){
return (i<<1)+2;
}
最大堆、最小堆
如果一个二叉堆满足,所有的子节点都不比父节点大,那么称为最大堆
相反,如果一个二叉堆所有子节点都不比父节点小,那么其为最小堆
建堆
问题:假设给你一个数组,怎样根据这个数组构建最大堆(最小堆),其时间复杂度为多少?
引论:维护堆的性质——heapify
给一个数组 A 和下标 i 数组的 left(i) 子树和 right(i) 子树部分都满足最大(小)堆的性质,而 i、left(i) 和 right(i) 三者有可能不满足,怎样对数据进行操作使得 i 子树可以满足堆的性质?以最大堆为例:
我们只需要对三个数值进行比较,将最大值与根节点交换即可。注意交换后其子节点原有的堆性质可能遭到破坏,所以形成了一个相似的子问题,对子问题递归进行求解即可完成全部的堆维护。
void maxHeapify(vector &v,size_t i){
T tmp=v[i];
size_t pos=i;
//选择三个节点中最大的
if(left(i)v[pos]){
pos=left(i);
}
if(right(i)v[pos]){
pos=right(i);
}
//进行交换并进行子问题递归求解
if(pos!=i){
v[i]=v[pos];
v[pos]=tmp;
maxHeapify(v,pos);
}
}
最小堆同理可得,此处略去。
我们这里分析一下其复杂度,最差的情况下其子问题的大小是原问题的2/3,这发生在子问题树全满而对称位置子树响应高度全空的情形:
而每次找出最小值并进行交换所花费时间为常量O(1),故我们有:
由分治问题Master公式(这个我们单独拿一篇blog细说)可得,其时间复杂度为O(lgn)
建堆——buildHeap
我们利用heapify来自下而上建堆,这需要满足使用heapify的条件。
对于一个堆状数组,其叶节点由于无儿子节点,所以显然满足堆的性质。所以我们从第一个可能不满足堆性质的非叶节点到根节点逐一进行heapify维护,就可以得到最后完整的堆。
void buildHeap(vector &v){
for(int i=v.size()/2-1;i>=0;i--){
maxHeapify(v,i);
}
}
一个buildHeap的例子如下图所示
[站外图片上传中...(image-7df3cc-1514818541338)]
其正确性由循环不变量“始终满足heapify条件“易证。
由于其对n/2个节点进行了maxHeapify操作,而每次maxHeapify最差情形耗时O(lgn),所以似乎整个buildHeap耗时O(nlgn),这的确是一个上界,但不是一个紧上界,这是因为并不是所有节点维护堆性质都需要递归O(lgn)深度,例如最底层非叶节点heapify顶多只需要1次调用即可完成,所以一个tight bound计算如下:
h表示节点距离底部距离,因为表示需要O(h)次调用的heapify的节点有n/2^(h+1)个,所以时间复杂度:
故对给定数组进行buildHeap其紧确界为O(n)
但是注意如果逐一添加元素自上而下构建堆,其时间复杂度则为O(nlgn)
应用
堆排序###
对于最大堆,我们将数组第一个元素取出即为整个数组的最大值,将最后一个元素换到数组头部,此时其满足heapify使用条件,对其进行堆维护可以继续得到一个堆(相比之前少了一个元素),递归这个过程可以逐一取出剩余数组的最大值,则可以得到排序后的结果。其有n次heapify调用,故其复杂度为O(nlgn)。注意到其操作是可以in-place进行的(只要将取出的最大值与堆尾交换即可),性质可以说是非常良好了。
top k问题###
问题:我们希望找到流数据中前k大的值,该怎么做?
维护一个size为k的最小堆,每次来新数据将其与堆顶作比较,如果比堆顶要大,则将堆顶替换(因为堆顶表示整个堆的最小元素,来了一个比它大的则其不可能为前k大的元素了)
同理求数据流前k小用最大堆。
优先级队列###
问题:对于一般的队列是先入先出,我们有时候需要一种队列,根据其key(优先级)来进行选择性出队,优先级高的先出队,而与插入顺序无关。例如医院病人排队是根据病情缓急来的,而与来的先后无关。
对于优先级队列我们底层使用堆来实现,因为堆天然维护了堆首为整个数组最值这一特性。
对于优先级队列,我们还需要为堆添加三个操作:
1.进队——push
首先将新的元素添加至数组最后,然后自底向下维护堆性质。其复杂度为O(lgn)
(当然也可以利用后面的increaseKey,首先将其优先级设置为无穷小,然后increaseKey到给定值,代码中没有使用这种实现方式因为考虑到泛型不好设置无穷小)
void push(const T& x){
heap_vector.push_back(x);
size_t i=heap_vector.size()-1;
while(i>0&&heap_vector[parent(i)]2.队首——max(min)
堆状数组第一个元素即为最值元素,返回第一个元素即可
T& max(){
return heap_vector[0];
}
3.出队——pop
其实可以删除优先级队列中任意位置的元素,只要将该位置元素与堆尾进行交换后删掉最后一个元素,然后维护该位置的堆性质即可。其发咋读为O(lgn)
作为一种特殊情形,出队只要先获取最大元素然后pop(0)即可。
void pop(size_t i){
heap_vector[i]=heap_vector.back();
heap_vector.pop_back();
maxHeapify(heap_vector,i);
}
4.提高优先级——increaseKey(视优先级定义有时也可以为decreaseKey,即越小优先级越高)
这个操作是必要的,因为有时候会需要改变队中已有元素的优先级,例如医院中排队中的某个病人突发病情加重需要。另外非常常见的一点是SSSP(Single Source Shortest Path)问题中若路径权重为非负值我们采用Dijkstra会需要更新元素的当前最短路径值。
对于最大堆来讲increaseKey可能会使得和其parent不满足堆性质,所以上浮逐一维护堆性质即可。其复杂度为O(lgn)。
void increaseKey(size_t i,const T& x){
if(heap_vector[i]0&&heap_vector[parent(i)] 结语
本文介绍了二叉堆的两种形式——最大堆和最小堆,以最大堆为例讲述了怎样建堆以及相关操作的复杂度分析。最后介绍了堆在实际问题中的三种应用。
二叉堆到这里基本就结束了,但堆却远没有结束,考虑下面两个问题:
1.给两个堆,怎样快速(O(lgn))将其合并?——二项堆
2.怎样快速decreaseKey?(O(lgn)不够快,希望摊还O(1))——斐波那契堆
后面会分多篇blog介绍这两种数据结构