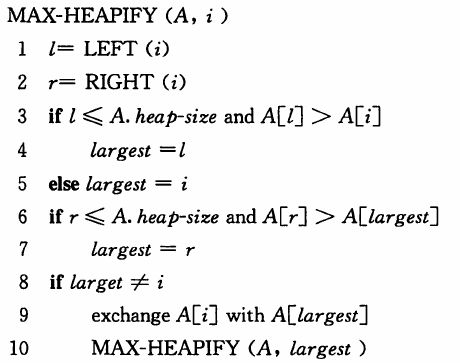第六章 堆排序

堆排序的时间复杂度与归并排序相同为O(nlg n)，空间复杂度与插入排序相同为O(1)。堆这种数据结构还用于优先队列，有时被引申为垃圾存储机制。

6.1 堆

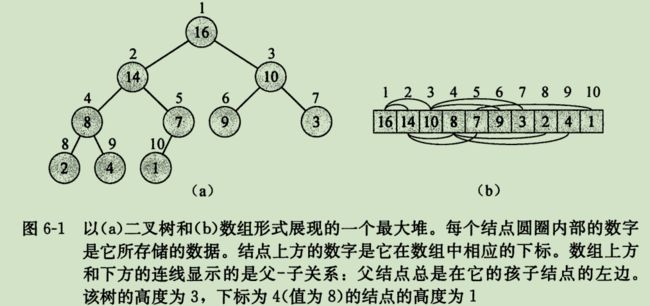
二叉堆是用数组组织的近似完全二叉树。除最底层外树是完全充满的。数组A两个属性：length表示空间大小，heap-size代表目前存储元素个数，0 <= A.heap-size <= A.length，根节点为A[1]。

给定结点下标i，易计算得父节点、左孩子右孩子下标：

堆分为最大堆和最小堆， 最大堆：某个结点的值至多与其父结点一样大。最小堆相反，常用于构造优先队列。堆中结点的高度为 该节点到叶节点最长简单路径上边的数目，堆的高度为根结点的高度。n个元素的堆高度为Θ(lg n)。

练习

6.1-1

答：最多时是满二叉树，共2^(h+1) − 1 ; 最少时最后一层只有一个结点，共2^h。

6.1-2

答：由上题可知

故 h = ⌞lg n⌟

6.1-3

答：定义可知。

6.1-4

答：最后一层。

6.1-5

答：从小到大的有序数组是。

6.1-6

答：不是。画图可知 6 是 7的parent。

6.1-7

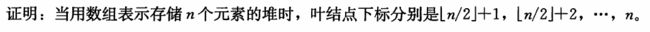
答：可知堆高度为⌞lg n⌟，故最后一层也就是叶子层以上共有结点

用 n 减就得到叶子数。

6.2 维护堆的性质

MAX-HEAPIFY作用于数组A和下标i，假定根节点为LEEF(i) 和RIGHT(i)的二叉树都是最大堆，通过让A[i]的值在最大堆中逐级下降使得以下标i为根节点的子树重新遵循最大堆的性质。LEFT(i)、RIGHT(i)即为上节中的两个函数，分别得到左、右子树根结点下标。
伪代码：

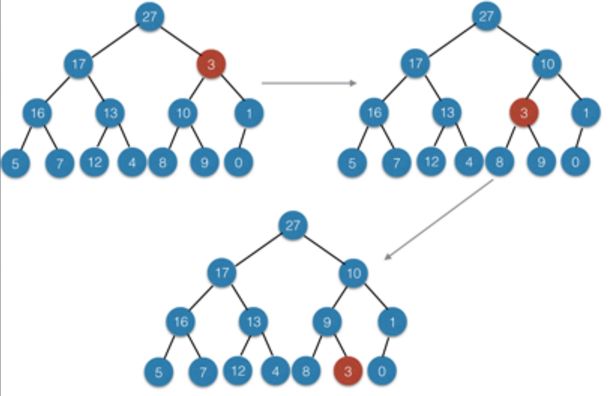
执行过程：

复杂度分析：对n个元素的子树代价包括调整A[i]、A[LEFT(i)]、A[RIGHT(i)]的关系O(1)，递归调用子树，每个子树大小至多2n /3，故递归式为：

由主定理可知T(n) = O(lg n)。所以树高为h 的结点MAX-HEAPIFY的复杂度为O(h)。

练习

6.2-1

6.2-2

伪代码：

MIN-HEAPIFY(A, i)
  l = LEFT(i)
  r = RIGHT(i)
  if l ≤ A.heap-size and A[l] < A[i]
      smallest = l
  else
      smallest = i
  if r ≤ A.heap-size and A[r] < A[smallest]
      smallest = r
  if smallest ≠ i
      exchange A[i] with A[smallest]
      MIN-HEAPIFY(A, smallest)

与维护最大堆的算法相比只是改了不等式符号，复杂度相同。

6.2-3

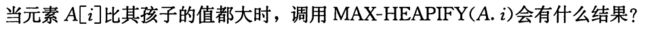
答：不做交换操作直接返回。

6.2-4

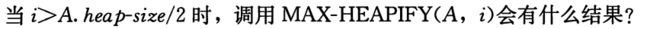
答：说明此为叶子结点，在第一个if的else处赋值后后面的条件都不满足，直接返回。

6.2-5

伪代码：

MAX-HEAPIFY(A, i):
    while True:
        l = LEFT(i)
        r = RIGHT(i)
        if l ≤ A.heap-size and A[l] > A[i]:
            largest = l
        else 
            largest = i
        if r ≤ A.heap-size and A[r] > A[largest]:
            largest = r
        if largest ≠ i:
            swap(A[i], A[largest])
            i = largest
        else 
            break

6.2-6

答：最坏情况下从根节点一直递归到叶节点，由于堆的高度为lgn，所以最坏运行时间是Ω(lgn)。

6.3 建堆

MAX-HEAPIFY可使指定结点满足堆的性质，所以可以利用这个过程建堆。本来是对n = A.length的每个元素调用，但是A(n/2 + 1.....n)都是叶子结点，所以只需要对其他结点调用即可。

伪代码：

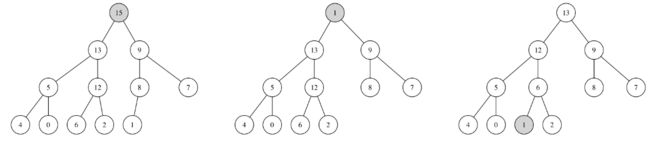
例子如下：

用循环不变量证明正确性：
这个过程的循环不变量是： 每一次for循环的开始，i + 1, i + 2......, n都是一个最大堆的根节点。
初始化：第一次循环前，i = n/2, i以后的结点都是叶子，故成立。
保持：因为结点 i 的孩子结点下标都更大，所以它们都是最大堆的根。MAX-HEAPIFY维护了结点 i + 1...n都是最大堆根结点的性质。
终止：终止时i = 0，所以1到n都是其后面结点的根节点。

算法复杂度分析：
但从代码来看，n 次调用O(lgn)的函数，复杂度上界O(nlgn)。事实上可推出紧确界O(n)，说明可以在线性时间内把一个无序数组构造成最大堆。

将调用的MAX-HEAPIFY换成MIN-HEAPIFY就可以构造最小堆。

练习

6.3-1

6.3-2

答：因为MAX-HEAPIFY是向叶子方向递归，只有其孩子结点都是最大堆的根时才能保证当前处理的结点会成为此子树的最大根。否则处理过的结点将不再改变，即使其孩子结点值更大。

6.3-3

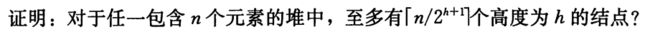
证明：设树高为h0, 则有

当h层满的时候达到最多。

6.4 堆排序算法结点

首先调用BUILD-MAX-HEAP将数组A[1..n]建成最大堆。然后每次取出根结点并将最后一个节点放到根的位置，再调用MAX-HEAPIFY使得结点到满足最大堆性质的位置。不断重复这个过程直到堆大小从n - 1降到2。
伪代码：

例子如下：

算法复杂度分析：n - 1次调用MAX-HEAPIFY，每次O(lgn)，共O(nlgn)。

练习

6.4-1

答：首先建堆，建好后排序过程如下：

6.4-2

初始化：开始时A[i+1...n]为空，故成立。
保持：A[1]是每次从剩下的元素中选出的根，所以是A[1...n]中最大的，取出后堆元素减一，剩下的i - 1个元素中由选出最大的放在A[1]。
终止：当i = 1时终止，此时堆只有一个元素所以最大，被选出的都是已排序的n - 1个元素。

6.4-3

答：如果是升序，是最坏情况，建堆需要O(n)，排序每次调用MAX-HEAPIFY都需要递归（n - 1）* lgn。降序时建堆不需要操作，但排序还是一样。故都是O(nlgn)。

6.4-4

答：最坏情况就是上题的升序。

6.4-5

6.5 优先队列

优先队列是一种用来维护由一组元素构成的集合S的数据结构，每个元素的值称为关键字。一个最大优先队列支持以下操作：

用最大堆来实现最大优先队列：

• 返回最大关键字元素的HEAP-MAXIMUM伪代码为：

HEAP-MAXIMUM(A)
    return A[1]

复杂度O(1)。

• 去掉并返回最大关键字元素的HEAP-EXTRACT-MAX:

HEAP-EXTRACT-MAX(A)
    if A.heap-size < 1
        error "heap underflow"
    max = A[1]
    A[1] = A[A.heap-size]
    A.heap-size = A.heap-size - 1
    MAX-HEAPIFY(A, 1)
    return max

复杂度为调用MAX-HEAPIFY的O(lgn)。

• 增加元素x关键字的HEAP-INCREASE-KEY(A, i, key):

HEAP-INCREASE-KEY(A, i, key)
    if key < A[i]
        error "new key is smaller than current key"
    A[i] = key
    while i > 1 and A[PARENT(i)] < A[i]
        exchange A[i] with A[PARENT(i)]
        i = PARENT(i)

因为更新关键字的结点到根节点的路径长度为O(lgn)，所以循环也只是lgn次，复杂度O(lgn)。

• 插入元素x的MAX-HEAP-INSERT:

MAX-HEAP-INSERT(A, key)
    A.heap-size = A.heap-size + 1
    A[A.heap-size] = -∞
    HEAP-INCREASE-KEY(A, A.heap-size, key)

复杂度同HEAP-INCREASE-KEY的O(lgn)。
所以在有n个元素的堆中，所有操作都可以在O(lgn)内完成。

练习

6.5-1

6.5-2

6.5-3

• HEAP-MINIMUM：

HEAP-MINIMUM(A)
    return A[1]

• HEAP-EXTRACT-MIN：

HEAP-EXTRACT-MIN(A)
    if A.heap-size < 1
        error "heap underflow"
    min = A[1]
    A[1] = A[A.heap-size]
    A.heap-size = A.heap-size - 1
    MIN-HEAPIFY(A, 1)
    return min

• HEAP-DECREASE-KEY：

HEAP-DECREASE-KEY(A, i, key)
    if key > A[i]
        error "new key is larger than current key"
    A[i] = key
    while i > 1 and A[PARENT(i)] > A[i]
        exchange A[i] with A[PARENT(i)]
        i = PARENT(i)

• MIN-HEAP-INSERT：

MIN-HEAP-INSERT(A, key)
    A.heap-size = A.heap-size + 1
    A[A.heap-size] = ∞
    HEAP-DECREASE-KEY(A, A.heap-size, key)

6.5-4

答：因为要调用HEAP-INCREASE-KEY。

6.5-5

初始时：只有新增大的元素可能不满足最大堆性质，故成立。
保持：每次不满足性质的结点都与其parent交换，然后定位到其parent。故违背的可能又变为此点与其parent。
终止：终止时要么到了根节点，此时由循环不变量可知所有点都满足最大堆性质。要么比其parent值小，此时也满足了最大堆性质。

6.5-6

改为：

HEAP-INCREASE-KEY(A, i, key):
    if key < A[i]
        error "New key is smaller than current key"
    A[i] = key
    while i > 1 and A[PARENT(i)] < key
        A[i] = A[PARENT(i)]
        i = PARENT(i)
    A[i] = key

6.5-7

答：优先队列按优先级高低控制进出顺序。设置优先级的时候，队列为先进的元素优先级高，栈是后进的优先级高。

6.5-8

伪代码：

HEAP-DELETE(A, i)
    if i > A.heap-size
        error "Beyond the scope of the heap"
    A[i] = A[A.heap-size]
    A.heap-size -= 1
    MAX-HEAPIFY(A, i)

6.5-9

答：首先将每个链表的第一个元素取出来加入大小为k的最小堆中，每次取堆的根加入结果链表。再选择该最小元素所在链表的下一个节点加入到堆中。同leetcode 的Merge k Sorted Lists一题。每个元素调用一次MIN-HEAPIFY操作，堆的大小为k，故复杂度O(knlgk)。具体分析代码见23. Merge k Sorted Lists

本章各函数代码实现

#include
using namespace std;

//下标从0开始
int Parent(int i)
{
    return (i - 1) / 2;
}

int Left(int i)
{
    return i * 2 + 1;
}

int Right(int i)
{
    return i * 2 + 2;
}

//递归调整位于i的元素
void MaxHeapify1(int a [], int n, int i)
{
    int l = Left(i);
    int r = Right(i);
    int largest = 0;
    if (l <= (n - 1) && a[l] > a[i])
        largest = l;
    else
        largest = i;
    if (r <= (n - 1) && a[r] > a[largest])
        largest = r;
    if ( largest != i)
    {
        swap(a[i], a[largest]);
        MaxHeapify1(a, n, largest);
    }
}

//非递归调整位于i的元素
void MaxHeapify2(int a [], int n, int i)
{
    while( true)
    {
        int l = Left(i);
        int r = Right(i);
        int largest = 0;
        if (l <= (n - 1) && a[l] > a[i])
            largest = l;
        else
            largest = i;
        if (r <= (n - 1) && a[r] > a[largest])
            largest = r;
        if ( largest != i)
        {
            swap(a[i], a[largest]);
            i = largest;
        }
        else
            break;
    }
}

void BuildMaxHeap(int a[], int n)
{
    int i;
    for (i = n / 2 - 1; i >= 0; i --)
        MaxHeapify1(a, n, i);
}

void HeapSort(int a[], int n)
{
    int i;
    BuildMaxHeap(a, n);
    for (i = n - 1; i >= 1; i --)
    {
        swap(a[0], a[i]);
        MaxHeapify1(a, --n, 0);
    }
}

//priority queue相关操作
int HeapMaximum(int a[])
{
    return a[0];
}

int HeapExtractMax(int a[], int n)
{
    if (n < 0)
    {
        cout<<"heap underflow";
        return -1;
    }
    int mx = a[0];
    a[0] = a[n - 1];
    MaxHeapify1(a, --n, 0);
    return mx;
}

void HeapIncreaseKey(int a[], int i, int key)
{
    if ( key < a[i])
    {
        cout<<"new key is smaller";
        return ;
    }
    a[i] = key;
    //采用插入排序循环的思想，一次赋值完成交换操作
    while ( i > 0 && a[ Parent(i) ] < key)
    {
        //swap(a[i], a[ Parent(i) ] );
        a[i] = a[ Parent(i) ];
        i = Parent(i);
    }
    a[i] = key;
}

void HeapInsert(int a[], int n, int key)
{
    //n = n + 1;
    a[n] = -1;
    HeapIncreaseKey(a, n, key);
}

void HeapDelete(int a[], int i, int n)
{
    if (i >= n)
    {
        cout<<"Beyond the scope";
        return ;
    }
    a[i] = a[n - 1];
    MaxHeapify1(a, --n, i);
}

void print(int a[], int n)
{
    for (int i = 0; i < n; i ++)
        cout << a[i] <<" " ;//<< "i ="<< i <<" ";
    cout << endl;
}

int main()
{
    int a[10] = {16,4,10,14,7,9,3,2,8,1};
    int b[10] = {16,14,10,8,7,9,3,2,4,1};
    //MaxHeapify2(a, 10, 1);
    //BuildMaxHeap( a, 10);
    //HeapSort(a, 10);
    //cout<

参考

https://ita.skanev.com/index.html
https://github.com/gzc/CLRS/