A: 给定一个最多包含40亿个随机排列的32位整数的顺序文件,找出一个不在文件中的3位为整数(在文件中至少缺失一个这样的数-为什么?)。在具有足够内存的情况下,如何解决该问题?如果有几个外部的“临时”文件可用,但是仅仅几百字节的内存,又该如何解决该问题?
至少缺失一个整数,因为一共有$2^32$也就是4294967296个这样的整数。
在不考虑内存的情况下可以使用第一章的位图技术。使用536870912个8位字节形成位图来表示已经看到的整数。
使用临时文件的话,就可以使用分趟来找出来缺失的整数。
代码如下:
//输入数据集合、集合长度、字节范围
int lostNumber(int numbers[],int numberLength,int localBits){
int oneArray[numberLength];
int zeroArray[numberLength];
int oneCount = 0;
int zeroCount = 0;
int lostNumber = 0 ;
int selectNumber = 0;
for (int bit = localBits - 1; bit >= 0; bit --) {
selectNumber = 1 << bit;
oneCount = 0;
zeroCount = 0;
for (int i = 0; i < numberLength; i ++) {
if (numbers[i] & selectNumber) {
oneArray[oneCount ++] = numbers[i];
}else{
zeroArray[zeroCount ++] = numbers[i];
}
}
if (oneCount > zeroCount) {
numbers = zeroArray;
numberLength = zeroCount;
}else{
lostNumber += selectNumber;
numbers = oneArray;
numberLength = oneCount;
}
}
return lostNumber;
}
实现:
//这里只是一个假设
int len = 13;
int maxBits = 4;
int arr[13] = {0,3,4,5,6,7,8,9,10,11,13,14,15};
int lostNum = lostNumber(arr,len,maxBits);
printf("lostNum=%d\n",lostNum);
B: 将一个n元一维向量向左旋转i个位置。例如,当n=8且i=3时,向量abcdefgh旋转为defghadc。简单的代码使用一个n元的中间向量在n步内完成该工作。你能否仅使用十个额外字节的存储空间,在正比于n的时间内完成向量的旋转。
虽然说可以想象出来这么做的原因,但是真想不起来要这么做。所以直接上代码:
int greatestCommonDivisor(int m,int n){
while (m != n) {
if (m > n) {
m -= n;
}else{
n -= m;
}
}
return m;
}
void rotatingVector(int array[],int rotate,int vector){
int gcd = greatestCommonDivisor(rotate, vector);
for (int i = 0; i < gcd; i ++) {
int temp = array[i];
int first = i;
int next = (i + rotate)%vector;
while (next != i) {
array[first] = array[next];
first = next;
next = (first + rotate)%vector;
}
array[first] = temp;
}
}
验证:
int array[10] = {1,2,3,4,5,6,7,8,9,10};
rotatingVector(array, 4, 10);
for (int i = 0; i < 10; i ++) {
printf("number=%d\n",array[i]);
}
C: 给定一个英语字典,找出其中所有变位词集合。例如:“pots”、“stop”和“tops”互为变位词。
为了找出给定单词的所有变位词,我们首先计算它的标识。如果不允许进行预处理,我们只能顺序读取整个字典,计算每个单词的标识并比较两个标识。如果允许进行与处理,我们可以在一个预先计算好的结构中执行二分搜索,该结构中包括按表示排序的对(标识、单词)。
下边是别人的实现分成两部分:
宏定义
#define WORDMAX 100
#define error( str ) fatal_error( str )
#define fatal_error( str ) fprintf( stderr, "%s\n", str ), exit( 1 )
获取单词到文件中:
//比较
int charcomp(const void* x, const void* y) { return *(char*)x - *(char*)y; }
//字符串大小写转换
char* mytolower(char* lword, char* word)
{
while ( *word != '\0' ){
if (isalpha(*word) && isupper(*word)){ *lword++ = tolower(*word++); }
else { *lword++ = *word++; }
}
*lword = '\0'; // 末尾加结束字符
return lword;
}
//获取单词标识并添加到文件中
void add_sign(FILE* rfile, FILE* wfile)
{
assert(rfile != NULL && wfile != NULL);
char word[WORDMAX], lword[WORDMAX], sign[WORDMAX];
while(fscanf(rfile, "%s", word) != EOF){
mytolower(lword, word);
strcpy(sign, lword);
qsort(sign, strlen(sign), sizeof(char), charcomp);
fprintf(wfile, "%s\t%s\r\n", sign, word);
}
return;
}
代码测试:
FILE* rfile = fopen("/Users/zhangguanqing/Downloads/Calculator/Calculator/dictionary.txt", "r");
if (NULL == rfile){ fatal_error("不能打开dictionary.txt文件!\n"); }
FILE* wfile = fopen("/Users/zhangguanqing/Downloads/Calculator/Calculator/sign_dictionary.txt", "w");
if (NULL == wfile){ fatal_error("不能打开sign_dictionary.txt文件!\n"); }
add_sign(rfile, wfile);
fclose(rfile);
fclose(wfile);
printf("生成完毕!!");
第二部分输出所有变位词:
void print_anagrams(FILE* rfile)
{
char word[WORDMAX], sign[WORDMAX];
multimap angrams;
std::set myset;
while(fscanf(rfile, "%s\t%s", sign, word) != EOF){
myset.insert(sign);
angrams.insert(std::make_pair(sign, word));
}
for (set::iterator iter = myset.begin(); iter != myset.end(); ++iter) {
multimap::iterator it = angrams.equal_range(*iter).first;
for (; it != angrams.equal_range(*iter).second; ++it){
std::cout << ' ' << (*it).second;
}
cout << endl;
}
return;
}
代码测试:
FILE* rfile = fopen("/Users/zhangguanqing/Downloads/CalculatorHelp/CalculatorHelp/sign_dictionary.txt", "r");
if (NULL == rfile){ fatal_error("不能打开sign_dictionary.txt文件!\n"); }
print_anagrams(rfile);
fclose(rfile);
printf("执行完毕!!");
- 考虑查找给定输入单词的所有变位词问题。仅给定单词和字典的情况下,如何解决问题?如果有一些时间可以在相应任何查询之前预先处理字典,又会如何?
见C。 - 给定包含4300000000个32位整数的顺序文件,如何找出一个出现至少出现两次的整数?
二分搜索通过递归搜索包含半数以上整数的子区间来查找至少出现两次的单词。我最初的解决方案不能保证每次迭代都将整数数目减半,所以log2n趟的最坏情况运行时间正比于nlogn。jim saxe经过观察发现,该搜索用不着考虑过多重复元素,从而可以把运行时间缩短为线性时间。如果他的搜索程序知道当前范围内m个整数中一定有重复元素,那么程序智慧在当前工作磁带上存储m+1个整数,此后过来的整数将会被丢弃。虽然他的方法经常会忽略输入变量,但其策略却足以保证至少找到一个重复元素。 - 前面设计了两个需要精巧代码来实现的向量旋转算法。将其分别作为独立的程序实现。在每个过程中,i和n的最大公约数如何实现?
方法一(杂耍算法):
见B。
方法二(求逆):
先局部翻转在整体翻转(例如abcdef:n=6,i=3。先翻转abc,再翻转def,最后翻转cbafed)
void Reverse(char* str,int start,int end)
{
char tmp;
int mid = (start + end)/2;
for (int i = start,j = end;i <= mid;i++,j--)
{
tmp = str[i];
str[i] = str[j];
str[j] = tmp;
}
}
//把字符串循环左移k位
void LeftRotateString(char* str,int k,int strLen)
{
Reverse(str,0,k-1);
Reverse(str,k,strLen-1);
Reverse(str,0,strLen-1);
}
测试:
char str[5] = "abcde";
LeftRotateString(str,3,5);
printf("%s\n",str);
方法三(块变换):
我们将旋转的向量x分成向量a和向量b,那么旋转向量x就相当于将向量ab两个部分旋转成向量ba。
假设a比b短(哪个长哪个分割)
1)将b分割成bl和br两个部分,使得br和a的长度一致。
2)交换a和br,即ablbr转换成了brbla。通过每次转换序列a就位于它最终的位置了。
3)然后类推我们再交换b的两个部分,可以使用递归来处理b部分。
代码实现:
/*
函数作用:把两块数据互换
arr:待翻转的字符串
aStart:第一块内容的起始位置
bStart:第二块内容的起始位置
len:交换的长度
*/
void swap(char* arr,int aStart,int bStart,int len)
{
assert(arr != NULL && aStart >= 0 && bStart >= 0 && len > 0);
char tmp;
while(len-- > 0)
{
tmp = arr[aStart];
arr[aStart] = arr[bStart];
arr[bStart] = tmp;
aStart++;
bStart++;
}
}
//待旋转字符串的起始位置start,长度len,向左移动的位数bits
void Rotate(char* str,int Start,int len,int bits)
{
//根据移动的位数,把待旋转字符串分成两部分
//左半部分
int leftStart = Start;
int leftLen = bits;
//右半部分
int rightLen = len - bits;
//待旋转字符串长度为1时,直接结束
if (1 == len)
{
return;
}
//旋转字符串
if (leftLen > rightLen)
{
swap(str,leftStart,leftStart + leftLen,rightLen);
Rotate(str,leftStart + rightLen,len - rightLen,len - 2 * rightLen);
}
else
{
swap(str,leftStart,leftStart + len - leftLen,leftLen);
Rotate(str,leftStart,len - leftLen,leftLen);
}
}
void LeftRotateString(char* str,int k,int strLen)
{
Rotate(str,0,strLen,k);
}
测试:
char str[10] = "abcdefghij";
LeftRotateString(str,3,10);
printf("%s",str);
- 几位读者指出,既然所有的三个旋转算法需要的运行时间都正比于n,杂技算法的运行速度显然市求逆算法的两杯。杂技算法对数组中的每个元素仅存储和读取一次,而求逆算法需要两次。在实际的计算机上进行试验以比较两者的速度差异,特别注意内存引用位置附近的变化。
这里直接附上作者的答案吧(很大一部分都直接照抄的答案,毕竟答案不错)。
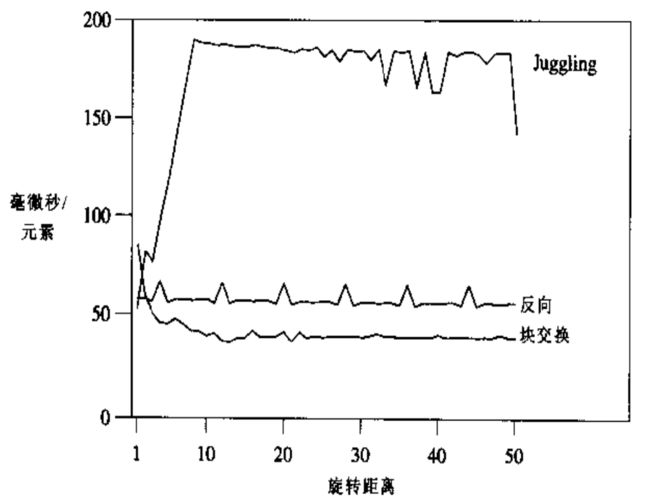
我在400MHz的pentium Ⅱ 机器上运行了三种所有算法,运行时把n固定为1000000,并使旋转距离从1变化到50。上图绘制了在每个数据集上50次运行的平均时间。求逆代码的运行时间比较一致,约为每个元素的58纳秒,仅当旋转距离模8余4时跳到需要66纳秒(这可能和32字节的缓存大小有关)。块交换的算法开始时开销最高(可能是由交换单位素块函数调用引起的),但是良好的高速缓存性能使得旋转距离大于2时该算法是最快的算法。杂技算法开始开销最低,但是由于其高速缓存性能很差(从每一个32字节的高速缓存线中访问单个元素),当旋转距离为8时所需要的时间接近200纳秒杂技算法的时间再190纳秒左右浮动,偶尔会有所下降(当旋转距离为1000时,它的运行时间会降到105纳秒,然后又恢复到190)。20世纪80年代中期,当旋转距离设置为页面大小时,这一代码使得页面的性能不稳定。 - 向量旋转函数将向量ab变为ba。如何将向量abc变为cba?(这对交换非相邻内存块的问题进行了建模)。
类似求逆,三个部分分别翻转,然后整体翻转。 - 20世纪70年代末期,贝尔实验室开发出了“用户操作的电话号码薄辅助程序”,该程序允许雇员使用标准的按键电话在公司电话号码薄中查找号码。要查找该系统设计者的名字Mike Lesk,可以按“Lesk* M * ”(也就是5375* M ),随后,系统会输出他的电话号码。这样的服务现在随处可见。该系统出现的一个问题是,不同名字可能具有相同的案件编码。在Lesk的系统中发生这种情况时,系统会询问用户更多的信息。给定一个大的名字文件(例如标准的大城市电话号码簿),如何定位这些“错误匹配”呢?(当Lesk在这种规模的电话簿上做实验时,他发现错误的匹配发生的概率仅仅是0.2%)。如何实现一个以名字的按键编码为参数,并返回所有可能的匹配名字的函数?
名字的标识是其按键编码,所以Lesk M * 的标识是“5375 * 6 *”。为了在字典中找出错误的匹配我们用按键编码来标识每个名字,并根据标识排序(当标识相同时根据名字排序),然后顺序读取排序后的文件并输出具有不同名字的顺序标识。为了检索给定按钮编码的名字,我们可以使用一种包含标识和其他数据的结构。尽管我们对该结构排序,然后使用二分法搜索查询按键编码;实际系统往往使用散列技术或数据库系统。 - 在20世纪60年代早期,Vic Vyssotsky与一个程序员一起工作,该程序员需要转置一个存储在才带上的4000*4000的矩阵(每条记录的格式相同,为数十字节)。他的同事基础提出的程序需要运行50个小时。Vyssotsky如何将运行时间减少到半个小时呢?
对对应的问题不理解,再遇到的时候再说吧。
为了转置行矩阵,Vyssotsky为每条记录插入列号和行号,然后调用系统的磁盘排序程序再按行排序,最后使用另一个程序删除列号和行号。 - 给定一个n元实数集合、一个实数t和一个整数k如何快速确定是否存在一个k元子集,其元素zhi he之和不超过t。
暂时搁置吧。。