声明!转载自:https://zhuanlan.zhihu.com/p/30116734,只为学习用,觉得写得通俗易懂,保留个笔记如有侵权联系立删
前言
StereoVision也就是我们常说的立体视觉,可以说是计算机视觉的一个重要模块。人类之所可以看到世界的各种各样的物品,正是得益于我们的视觉系统。那么,我们要想让机器人跟人一样可以分辨物体,同样的需要给机器人双眼。我们肯定都有这样的体验,当我们看到一个物体的时候,我们其实是可以估计出这个物体是离我们比较近还是比较远的,那我们需要给机器人的不仅仅是能够识别物体的系统,而且这种系统同样的要能够判断出障碍物距离有多远,立体视觉系统的功能就能够很好的满足要求。
立体视觉原理
一般而言,立体视觉系统需要有两个(或者两个以上)摄像头的支持,也就正如人类的双眼一样。下面首先介绍一下单目系统。
- 单目系统
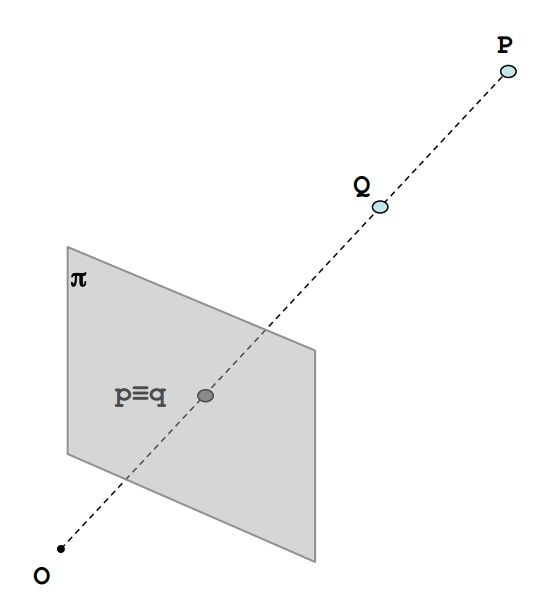
O点为相机的光心,π是摄像头的成像平面。从图中可以看出,如果P点与Q点在同一条直线上,那么他们在图像上的成像点就是同一个点,也就是 ,那么也就看不出来他们在距离上的差异(也就无法知道Q在前还是P在前)
- 双目系统
正是在发现了单目系统的缺陷之后,我们将系统由一个摄像头增加到两个摄像头,这样也就构成了一个立体系统。如果我们可以在两幅图像中找到对应点,我们就可以通过三角测量的方法来求得深度。
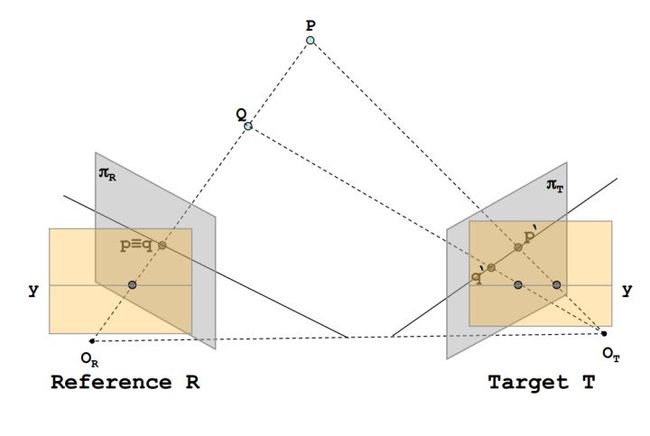
从图中可以很明显的看出,在增加了一个摄像头之后,P与Q在目标面T上的成像不在位于同一个点,而是有自己分别的成像点,也就是 与 。那么,在我们给出了Reference与Target之后,我们应该如何解决参考面与目标面之间的对应关系呢?
这个时候,就需要对极约束,对极约束意味着一旦我们知道了立体视觉系统的对极几何之后,对两幅图像间匹配特征的二维搜索就转变成了沿着极线的一维搜索。
图中黑色实线为R平面一条极线,绿色为T平面一条极线。给定一幅图像上的一个特征,它在另一幅图像上的匹配视图一定在对应的极线上(图中将P,Q视为特征,可以看到在T上的成像在绿色直线上)
通常我们使用的立体视觉系统都是比较标准的系统,如图所示。
一旦我们知道了对应点的搜索区域,就可以将其从2D降到1D,这样就形成了更加方便的立体视觉,对应点都被约束再同一条极线上,也就是图中的y直线。下面给出一个实际的示例(在理想情况下,我们希望两个摄像头的参数是完全一致的,并且两个相机的位置是平行的)。
- 视差与深度计算原理
在我们已经确保两个摄像头的参数是完全一致的,并且两者的位置是平行之后,我们的关注点就落到了如何计算物体的深度信息,这也是最重要最关键的地方。下面给出的是标准立体视觉系统下的计算原理。
我们假设 为空间中的一点, 为左边摄像头的光心, 为右边摄像头的光心,摄像头的焦距为 (光心到成像平面的距离),成像平面在图中用粉色线表示, 表示两个摄像头光心之间的距离,也称为基线, 在左右两个摄像机成像平面上的成像点分别为 与 , 与 为成像点的水平方向的距离(通常我们得到的是像素坐标系下的 坐标,其单位为像素,因此需要转换为实际的物理长度,涉及到坐标系的转换问题), 就是我们需要求的深度。
根据三角形相似定理( ):
,也就是我们通常所说的视差(disparity )。
我们可以发现,深度 是跟视差 成反比关系的,当视差 越小时, 越大,物体离立体视觉系统也就越远, 当视差 越大, 越小,物体离立体视觉系统也就越近。这一点和我们人眼系统是一样的,当我们观察离我们比较近的物体的时候,视差很大,可以获得的信息也就越多,当物体离我们很远的时候,视差很小,我们获得的信息也就很少了。
在图像处理中,我们通常用灰度值来表示视差信息,视差越大,其灰度值也就越大,在视差图像的视觉效果上表现出来就是图像越亮,物体离我们越远,其视差越小,灰度值也越小,视差图像也就越暗。
本文主要参考Stefano Mattoccia教授的PPT:Stereo Vision:Algorithms and Applications