理解GCN(一):从拉普拉斯矩阵到谱聚类
1 什么是GCN:
了解GCN之前必须对离散卷积(或者说CNN中的卷积)有一个明确的认识:
这篇博客介绍了卷积的简单理解,离散卷积本质就是一种加权求和。
以下介绍离散卷积的篇幅参考了这篇文章的第一部分:
如图1所示,CNN中的卷积本质上就是利用一个共享参数的过滤器(kernel),通过计算中心像素点以及相邻像素点的加权和来构成feature map实现空间特征的提取,当然加权系数就是卷积核的权重系数。
那么卷积核的系数如何确定的呢?是随机化初值,然后根据误差函数通过反向传播梯度下降进行迭代优化。卷积核的参数通过优化求出才能实现特征提取的作用,GCN的理论很大一部分工作就是为了引入可以优化的卷积参数。
 图1 CNN中卷积提取feature map示意图
图1 CNN中卷积提取feature map示意图
2.GCN中的Graph指什么?为什么要研究GCN?
因为在传统的CNN处理图像过程中,卷积核确实有效的提取了图像的空间特征。但是这些图像数据中的像素点是排列整齐的矩阵 (称为Euclidean Structure)。但是社交网络等网络结构有很多Non Euclidean Structure的数据,图论里称这种网络结构为拓扑结构,对应的图模型为拓扑图。
所以,Graph Convolutional Network中的Graph是指数学(图论)中的用顶点和边建立相应关系的拓扑图。
相比于GCN,CNN不能够在Non Euclidean Structure的数据上保持平移不变性:在拓扑图中每个顶点的邻接节点数目可能不同,因此无法用一个尺寸的卷积核进行卷积计算。所以我们考虑用GCN在这种NES的数据结构(拓扑图)上提取空间特征进行training。
In general,任何数据在赋范空间内都可以建立拓扑关联。这也是谱聚类的思想。
2.1 从拉普拉斯矩阵说到谱聚类
2.1.1 谱图理论
在对图进行建模成矩阵之前,我们要先了解特征值和特征向量的物理意义。
特征值与特征向量的定义式就是这样的:

特征值分解:
我们知道,对于矩阵A可以对角化的话,可以通过相似矩阵进行下面这样的特征值分解:
A = P Λ P − 1 A=P\Lambda P^{-1} A=PΛP−1其中 Λ \Lambda Λ为对角阵, P P P的列向量是单位化的特征向量。

对于方阵而言,矩阵不会进行纬度的升降,所以矩阵代表的运动实际上只有两种:
- 旋转
- 拉伸
最后的运动结果就是这两种的合成。
我们再回头看下刚才的特征值分解,实际上把运动给分解开了:

我们来看看在几何上的表现是什么,因此相似矩阵涉及到基的变换,所以注意观察基:
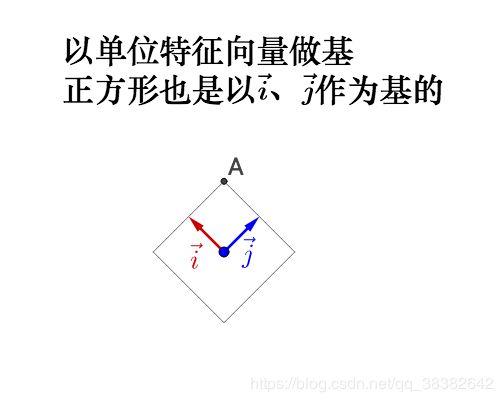
左乘 P = [ − 2 2 2 2 2 2 2 2 ] : P=\begin{bmatrix}\frac{-\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\\\frac{\sqrt{2}}{2}&\frac{\sqrt{2}}{2}\end{bmatrix}: P=[2−2222222]:
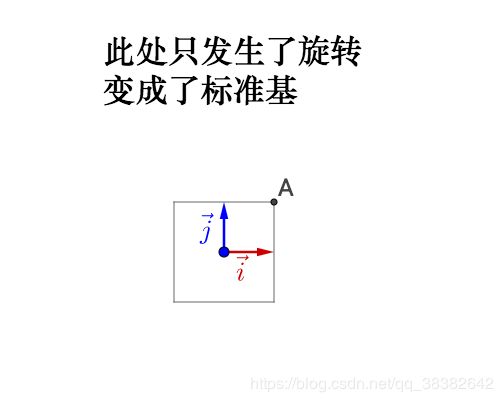
如果旋转前的基不正交,旋转之后变为了标准基,那么实际会产生伸缩,所以之前说的正交很重要。
继续左乘对角矩阵 Λ = [ 3 0 0 1 ] : \Lambda=\begin{bmatrix}3&0\\0&1\end{bmatrix}: Λ=[3001]:

相当于,之前的旋转指明了拉伸的方向,所以我们理解了:
- 特征值 λ \lambda λ就是拉伸的大小\
- 特征向量 P P P指明了拉伸的方向
回到我们之前说的运动上去,特征值就是运动的速度,特征向量就是运动的方向,而其余方向的运动就由特征向量方向的运动合成。所以最大的特征值对应的特征向量指明了运动速度的最大方向。
但是,重申一下,上面的推论有一个重要的条件,特征向量正交,这样变换后才能保证变换最大的方向在基方向。如果特征向量不正交就有可能不是变化最大的方向,比如:

所以我们在实际应用中,都要去找正交基。但是特征向量很可能不是正交的,那么我们就需要奇异值分解了。
那么如果我们对一个向量持续地去乘以A会发生什么?我们发现,经过不断的运动,变换后的向量会收敛到特征值最大的特征向量上:

特征值和特征向量的相关知识帮助理解图谱理论:https://zhuanlan.zhihu.com/p/80817719
以及谱聚类方法推导:
https://zhuanlan.zhihu.com/p/81502804
其中需要关注的几句话:
随着k趋于无穷,特征值最大的特征向量将会主宰其余的特征向量,从而v与特征值最大的u变成同一个方向!
通过这样的变换,我们甚至能够知道v的运动过程其实是由各个不同大小的特征值与特征向量控制的。
当x的取值在一个由K个特征向量张成的子空间中, x T M x x T x \frac{{x}^TMx}{x^Tx} xTxxTMx 的最大值恰好等于特征值。
当M等于标准化的laplace矩阵L时,若设 x ∈ { 0 , 1 } V x\in \{ 0,1\}^V x∈{0,1}V,(用1表示A类结点,用0表示B类结点),那么这A,B两类结点把他切割开,于是 x T M x x^TMx xTMx就表示切割开A,B图所经过的边数。因为我们可以利用上面的0,1代表连接与否,以及连接时 A i j = 1 / d A_{ij}=1/d Aij=1/d的情形,用 x T L x = 1 d ∑ { u , v } ∈ E ( x u − x v ) 2 x^TLx=\frac{1}{d} \sum_{\{u,v\}\in E}(x_u-x_v)^2 xTLx=d1{u,v}∈E∑(xu−xv)2来描述连接与否