ID3（Iterative Dichotomiser 3）算法原理详解

1.信息熵

熵这个概念最早起源于物理学，在物理学中是用来度量一个热力学系统的无序程度，而在信息学里面，熵是对不确定性的度量。在1948年，香农引入了信息熵，将其定义为离散随机事件出现的概率，一个系统越是有序，信息熵就越低，反之一个系统越是混乱，它的信息熵就越高。所以信息熵可以被认为是系统有序化程度的一个度量。

假设变量 X X 的随机取值为 X= X = { x1,x2,...,xn x 1 , x 2 , . . . , x n },每一种取到的概率分别是{ p1,p2,p3,...pn p 1 , p 2 , p 3 , . . . p n },则变量 X X 的熵为:

H(X)=−∑i=1npilog2pi H ( X ) = − ∑ i = 1 n p i l o g 2 p i

意思就是一个变量的变化情况越多，那么信息熵越大越不稳定。

2.信息增益

信息增益针对单个特征而言,即看一个特征t,系统有它和没有它时信息熵之差。下面是weka中的一个数据集,关于不同天气是否打球的例子。特征是天气,label是是否打球。

outlook	temperature	humidity	windy	play
sunny	hot	high	FALSE	no
sunny	hot	high	TRUE	no
overcast	hot	high	FALSE	yes
rainy	mild	high	FALSE	yes
rainy	cool	normal	FALSE	yes
rainy	cool	normal	TRUE	no
overcast	cool	normal	TRUE	yes
sunny	mild	high	FALSE	no
sunny	cool	normal	FALSE	yes
rainy	mild	normal	FALSE	yes
sunny	mild	normal	TRUE	yes
overcast	mild	high	TRUE	yes
overcast	hot	normal	FALSE	yes
rainy	mild	high	TRUE	no

共有14个样本，9个正样本(yes)5个负样本(no)，信息熵为:

Entropy(S)=−914log2914−514log2514=0.940286 E n t r o p y ( S ) = − 9 14 l o g 2 9 14 − 5 14 l o g 2 5 14 = 0.940286

接下来会遍历outlook, temperature, humidity, windy四个属性，求出用每个属性划分以后的信息熵假设以outlook来划分,此时只关心outlook这个属性，而不再关心其他属性:

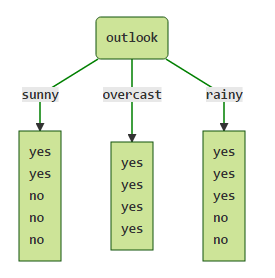
此时的信息熵为:

Entropy(sunny)=−25log225−35log235=0.970951 E n t r o p y ( s u n n y ) = − 2 5 l o g 2 2 5 − 3 5 l o g 2 3 5 = 0.970951

Entropy(overcast)=−44log244−0×log20=0 E n t r o p y ( o v e r c a s t ) = − 4 4 l o g 2 4 4 − 0 × l o g 2 0 = 0

Entropy(rainy)=−25log225−35log235=0.970951 E n t r o p y ( r a i n y ) = − 2 5 l o g 2 2 5 − 3 5 l o g 2 3 5 = 0.970951

总的信息熵为

Entropy=∑ti=t0tnP(t=ti)Entropy(T=ti) E n t r o p y = ∑ t i = t 0 t n P ( t = t i ) E n t r o p y ( T = t i )

即

Entropy(S|outlook)=P(sunny)×Entropy(sunny)+P(overcast)×Entropy(overcast)+P(rainy)×Entropy(rainy)=0.693536 E n t r o p y ( S | o u t l o o k ) = P ( s u n n y ) × E n t r o p y ( s u n n y ) + P ( o v e r c a s t ) × E n t r o p y ( o v e r c a s t ) + P ( r a i n y ) × E n t r o p y ( r a i n y ) = 0.693536

Entropy(S|outlook) E n t r o p y ( S | o u t l o o k ) 指的是选择属性 Outlook O u t l o o k 作为分类条件的信息熵,最终属性 Outlook O u t l o o k 的信息增益为:

IG(outlook)=Entropy(S)−Entropy(S|outlook)=0.24675 I G ( o u t l o o k ) = E n t r o p y ( S ) − E n t r o p y ( S | o u t l o o k ) = 0.24675

IG：Information Gain(信息增益)

同理可以计算选择其他分类属性的信息增益，选择信息增益最大的属性作为分类属性。分类完成之后，样本被分配到3个叶子叶子节点：

outlook	temperature	humidity	windy	play
sunny	hot	high	FALSE	no
sunny	hot	high	TRUE	no
sunny	mild	high	FALSE	no
sunny	cool	normal	FALSE	yes
sunny	mild	normal	TRUE	yes

outlook	temperature	humidity	windy	play
overcast	mild	high	TRUE	yes
overcast	hot	normal	FALSE	yes
overcast	cool	normal	TRUE	yes
overcast	hot	high	FALSE	yes

outlook	temperature	humidity	windy	play
rainy	mild	high	TRUE	no
rainy	mild	normal	FALSE	yes
rainy	mild	high	FALSE	yes
rainy	cool	normal	FALSE	yes
rainy	cool	normal	TRUE	no

当子节点只有一种 label l a b e l 时分类结束。若子节点不止一种 label l a b e l ，此时再按上面的方法选用其他的属性继续分类，直至结束。

3.ID3算法总结

IG(S|t)=Entropy(S)−∑value(T)|Sv|SEntropy(Sv) I G ( S | t ) = E n t r o p y ( S ) − ∑ v a l u e ( T ) | S v | S E n t r o p y ( S v )

IG: Information Gain(信息增益)

其中 S S 为全部样本集合， value(T) v a l u e ( T ) 属性 T T 的所有取值集合， v v 是 T T 的其中一个属性值， Sv S v 是 S S 中属性 T T 的值为v的样例集合， |Sv| | S v | 为 Sv S v 中所含样例数。在决策树的每一个非叶子结点划分之前，先计算每一个属性所带来的信息增益，选择最大信息增益的属性来划分，因为信息增益越大，区分样本的能力就越强。

注意: ID3只能正对nominal attribute，即标称属性