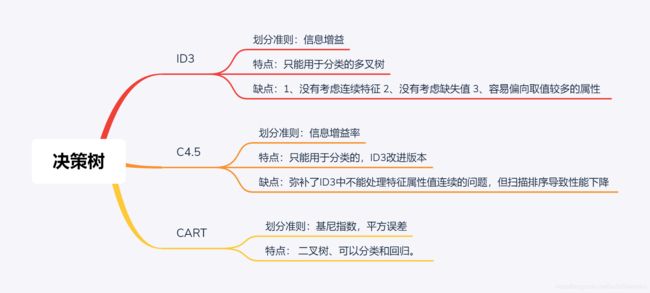
决策树中的ID3、C4.5和CART算法的对比分析
ID3算法(Iterative Dichotmizer 3)
1、 特征选择准则:信息增益
2、 特征必须离散化,不能处理连续值
3、不能处理缺失值
4、 偏向于选择取值多的属性
5、是一个多叉树模型,只用于分类
信息熵: 度量样本集合纯度最常用的一种指标,定义如下
Ent ( D ) = − ∑ k = 1 ∣ Y ∣ p k log 2 p k \operatorname{Ent}(D)=-\sum_{k=1}^{|\mathcal{Y}|} p_{k} \log _{2} p_{k} Ent(D)=−k=1∑∣Y∣pklog2pk
其中, D = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x m , y m ) } D=\left\{\left(\boldsymbol{x}_{1}, y_{1}\right),\left(\boldsymbol{x}_{2}, y_{2}\right), \ldots,\left(\boldsymbol{x}_{m}, y_{m}\right)\right\} D={(x1,y1),(x2,y2),…,(xm,ym)}表示样本集合, ∣ Y ∣ |\mathcal{Y}| ∣Y∣表示样本类别总数, p k p_{k} pk表示第 k k k类样本所占的比例,且 0 ≤ p k ≤ 1 0 \leq p_{k} \leq 1 0≤pk≤1 , ∑ k = 1 ∣ Y ∣ p k = 1 \sum_{k=1}^{|\mathcal{Y}|} p_{k}=1 ∑k=1∣Y∣pk=1。 Ent ( D ) \operatorname{Ent}(D) Ent(D)值越小,纯度越高。
条件熵:条件熵——在已知样本属性a的取值情况下,度量样本集合纯度的一种指标。
H ( D ∣ a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Ent ( D v ) H(D | a)=\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Ent}\left(D^{v}\right) H(D∣a)=v=1∑V∣D∣∣Dv∣Ent(Dv)
其中, a a a表示样本的某个属性,假定属性 a a a有 V V V个可能的取值 { a 1 , a 2 , … , a V } \left\{a^{1}, a^{2}, \ldots, a^{V}\right\} {a1,a2,…,aV},样本集合 D D D中在属性 a a a上取值为 a v a^{v} av的样本记为 D v D^{v} Dv, Ent ( D v ) \operatorname{Ent}\left(D^{v}\right) Ent(Dv)表示样本集合 D v D^{v} Dv的信息熵。 H ( D ∣ a ) H(D | a) H(D∣a)值越小,纯度越高。
C4.5算法(Iterative Dichotmizer 3)
1、 特征选择准则:信息增益率
2、 核心是ID3算法的改进版本
3、弥补了ID3算法中不能处理特征属性值连续的问题,需要扫描排序,会使C4.5性能下降
4、通过一种概率权重(Probability weights)的方法来处理缺失值
5、是一个多叉树模型,只用于分类
信息增益率
Gain_ratio ( D , a ) = Gain ( D , a ) IV ( a ) \text { Gain\_ratio }(D, a)=\frac{\operatorname{Gain}(D, a)}{\operatorname{IV}(a)} Gain_ratio (D,a)=IV(a)Gain(D,a)
其中
I V ( a ) = − ∑ v = 1 V ∣ D v ∣ ∣ D ∣ log 2 ∣ D v ∣ ∣ D ∣ I V(a)=-\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \log _{2} \frac{\left|D^{v}\right|}{|D|} IV(a)=−v=1∑V∣D∣∣Dv∣log2∣D∣∣Dv∣
CART决策树(classification and regression tree,CART)
1、特征选择准则:分类树用基尼指数最小化准则,回归树用平方误差最小化准则
2、可用于分类和回归问题,且每个特征可以被重复利用
3、一颗二叉树,二元切分法
4、ID3和C4.5通过剪枝来权衡树的准确性和泛化能力。而CART直接利用全部数据发现所有可能的树结构进行对比
5、采用替代划分(surrogate splits)的方式来处理缺失值
基尼值:基尼值反映了从数据集 D D D中随机抽取两个样本,其类别标记不一致的概率。
Gini ( D ) = ∑ k = 1 ∣ Y ∣ ∑ k ′ ≠ k p k p k ′ = ∑ k = 1 ∣ Y ∣ p k ∑ k ′ ≠ k p k ′ = ∑ k = 1 ∣ Y ∣ p k ( 1 − p k ) = 1 − ∑ k = 1 ∣ Y ∣ p k 2 \operatorname{Gini}(D)=\sum_{k=1}^{|\mathcal{Y}|} \sum_{k^{\prime} \neq k} p_{k} p_{k^{\prime}}=\sum_{k=1}^{|\mathcal{Y}|} p_{k} \sum_{k^{\prime} \neq k} p_{k^{\prime}}=\sum_{k=1}^{|\mathcal{Y}|} p_{k}\left(1-p_{k}\right)=1-\sum_{k=1}^{|\mathcal{Y}|} p_{k}^{2} Gini(D)=k=1∑∣Y∣k′=k∑pkpk′=k=1∑∣Y∣pkk′=k∑pk′=k=1∑∣Y∣pk(1−pk)=1−k=1∑∣Y∣pk2
基尼指数
Gini_index ( D , a ) = ∑ v = 1 V ∣ D v ∣ ∣ D ∣ Gini ( D v ) \operatorname{Gini\_index}(D, a)=\sum_{v=1}^{V} \frac{\left|D^{v}\right|}{|D|} \operatorname{Gini}\left(D^{v}\right) Gini_index(D,a)=v=1∑V∣D∣∣Dv∣Gini(Dv)
基尼值和基尼指数越小,样本集合纯度越高。
CART回归树划分准则
a ∗ , a ∗ v = arg min a , a v [ min c 1 ∑ x i ∈ D 1 ( a , a v ) ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ D 2 ( a , a v ) ( y i − c 2 ) 2 ] a_{*}, a_{*}^{v}=\underset{a, a^{v}}{\arg \min }\left[\min _{c_{1}} \sum_{\boldsymbol{x}_{i} \in D_{1}\left(a, a^{v}\right)}\left(y_{i}-c_{1}\right)^{2}+\min _{c_{2}} \sum_{\boldsymbol{x}_{i} \in D_{2}\left(a, a^{v}\right)}\left(y_{i}-c_{2}\right)^{2}\right] a∗,a∗v=a,avargmin⎣⎡c1minxi∈D1(a,av)∑(yi−c1)2+c2minxi∈D2(a,av)∑(yi−c2)2⎦⎤
根据上述公式找出最优划分特征 a ∗ a_{*} a∗和最优划分点 a ∗ v a_{*}^{v} a∗v 。其中, D 1 ( a , a v ) D_ {1} \left (a, a^{v}\right) D1(a,av)表示在属性 a a a上取值小于等于 a v a^{v} av的样本集合, D 2 ( a , a v ) D_ {2}\left(a, a^{v}\right) D2(a,av)表示在属性 a a a上取值大于 a v a^{v} av的样本集合, c 1 c_{1} c1表示 D 1 D_ {1} D1的样本输出均值, c 2 c_ {2} c2表示 D 2 D_{2} D2的样本输出均值。