Matlab中S-函数的编写
S-函数使Simulink的功能大大扩充,除Mmatlab外,用户还可以用其他语言(C/C++/FORTRAN/Ada)编写实现算法,很强大的同时也对使用者提出了较高的要求。下面是编写S-函数的整个流程:
0 基础知识
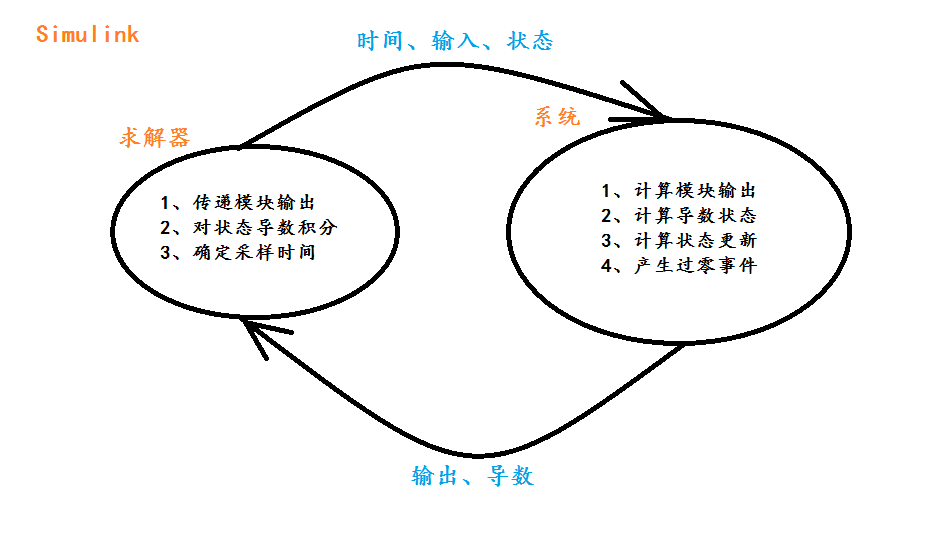
Simulnk仿真分为两步:初始化、仿真循环。仿真是由求解器控制的,求解器主要作用是:计算模块输出、更新模块离散状态、计算连续状态。求解器传递给系统的信息包括:时间、输入和当前状态。系统的作用:计算模块的输出、更新状态、计算状态导数,然后将这些信息传递给求解器。求解器和系统之间的信息传递是通过不同标志来控制的。
(2)S-函数控制流
(3)S-函数的几个概念
1) 直接馈通
在编写S-函数时,初始化函数中需要对sizes.DirFeedthrough 进行设置,如果输出函数mdlOutputs或者对于变采样时间的mdlGetTimeOfNextVarHit是输入u的函数,则模块具有直接馈通的特性sizes.DirFeedthrough=1;否则为0。
2) 采样时间
仿真步长就是整个模型的基础采样时间,各个子系统或模块的采样时间,必须以这个步长为整数倍。
连续信号和离散信号对计算机而言其实都是采样而来的,只是采样时间不同,连续信号采样时间可认为趋于0且基于微分方程,离散信号采样时间比较长基于差分方程。离散信号当前状态由前一个时刻的状态决定,连续信号可以通过微分方程计算得到。如果要将连续信号离散化还要考虑下信号能否恢复的问题,即香农定理。
采样时间点的确定:下一个采样时间=(n*采样间隔)+ 偏移量,n表示当前的仿真步,从0开始。
对于连续采样时间,ts可以设置为[0 0],其中偏移量为0;
对于离散采样时间,ts假设为[0.25 0.1],表示在S-函数仿真开始后0.1s开始每隔0.25s运行一次,当然每个采样时刻都会调用mdlOutPuts和mdlUpdate函数;
对于变采样时间,即离散采样时间的两次采样时间间隔是可变的,每次仿真步开始时都需要用mdlGetTimeNextVarHit计算下一个采样时间的时刻值。ts可以设置为[-2 0]。
对于多个任务,每个任务都可以以不同的采样速率执行S-函数,假设任务A在仿真开始每隔0.25s执行一次,任务B在仿真后0.1s每隔1s执行一次,那么ts设置为[0.25 0.1;1.0 0.1],具体到S-函数的执行时间为[0 0.1 0.25 0.5 0.75 1.0 1.1…]。
如果用户想继承被连接模块的采样时间,ts只要设置为[-1 0]。
1 S-函数的编写
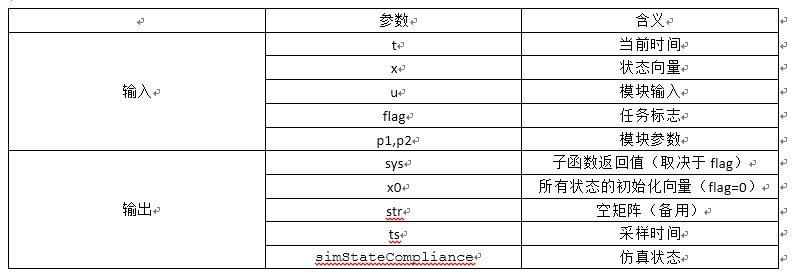
1.1 S函数的输入输出参数含义
首先打开M-文件的模版函数:function[sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag)
这个是无参的,如果有参数格式为:function[sys,x0,str,ts,simStateCompliance] = sfuntmpl(t,x,u,flag,p1,p2,...)
1.2 子函数的作用
(1)
function[sys,x0,str,ts,simStateCompliance]=mdlInitializeSizes
sizes = simsizes;
sizes.NumContStates = 0; %连续状态个数
sizes.NumDiscStates = 0; %离散状态个数
sizes.NumOutputs = 0; %输出个数
sizes.NumInputs = 0; %输入个数
sizes.DirFeedthrough = 1; %是否直接馈通
sizes.NumSampleTimes = 1; %采样时间个数,至少一个
sys = simsizes(sizes); %将size结构传到sys中
x0 = []; %初始状态向量,由传入的参数决定,没有为空
str = [];
ts = [0 0]; %设置采样时间,这里是连续采样,偏移量为0
% Specify the blocksimStateCompliance. The allowed values are:
% 'UnknownSimState', < The defaultsetting; warn and assume DefaultSimState
% 'DefaultSimState', < Same sim state as abuilt-in block
% 'HasNoSimState', < No sim state
% 'DisallowSimState' < Error out whensaving or restoring the model sim state
simStateCompliance = 'UnknownSimState';
(2)
functionsys=mdlGetTimeOfNextVarHit(t,x,u)
sampleTime = 1; % Example, set the next hit to be one secondlater.
sys = t + sampleTime;
(3)
functionsys=mdlOutputs(t,x,u)
sys = [];
(4)
function sys=mdlUpdate(t,x,u)
sys = [];
(5)
functionsys=mdlDerivatives(t,x,u)
sys = [];
(6)
functionsys=mdlTerminate(t,x,u)
sys = [];
2 实例解析
在编写S-函数之前要确定系统是否有状态变量、是连续还是离散状态以及输入输出个数、是否传入参数、采样时间等因素,针对不同的系统进行初始化、编写不同的子函数。
以matlab自带的限制积分函数程序limintm为例,讲解S-函数的编写。
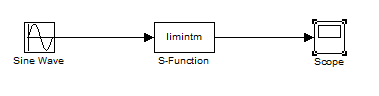
Simulink系统:
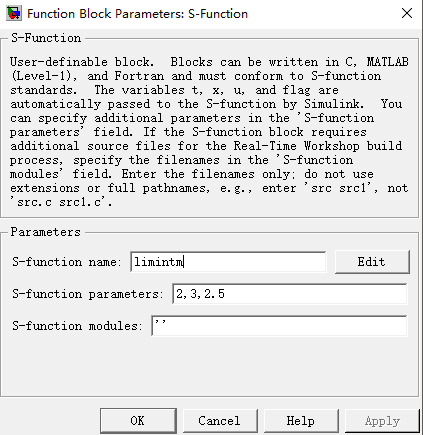
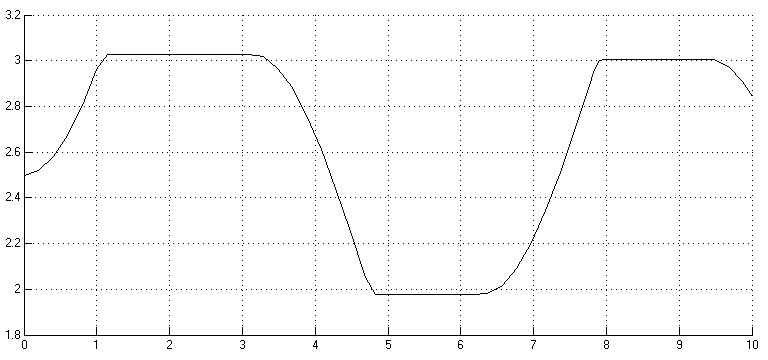
S-函数设置:其中传入的参数2,3,2.5分别表示为积分上限、积分下限和初始积分条件。
输出图形:
S-函数分析:
function [sys,x0,str,ts,simStateCompliance]=limintm(t,x,u,flag,lb,ub,xi)
%传入的三个参数放在后面lb,ub,xi的位置
%LIMINTM Limited integrator implementation.
% Example MATLAB file S-function implementing a continuous limited integrator
% where the output is bounded by lower bound (LB) and upper bound (UB)
% with initial conditions (XI).
%
% See sfuntmpl.m for a general S-function template.
%
% See also SFUNTMPL.
% Copyright 1990-2009 The MathWorks, Inc.
% $Revision: 1.1.6.2 $
switch flag
%%%%%%%%%%%%%%%%%%
% Initialization %
%%%%%%%%%%%%%%%%%%
case 0
[sys,x0,str,ts,simStateCompliance] = mdlInitializeSizes(lb,ub,xi);
%%%%%%%%%%%%%%%
% Derivatives %
%%%%%%%%%%%%%%%
case 1
sys = mdlDerivatives(t,x,u,lb,ub);
%%%%%%%%%%%%%%%%%%%%%%%%
% Update and Terminate %
%%%%%%%%%%%%%%%%%%%%%%%%
case {2,9}
sys = []; % do nothing
%%%%%%%%%%
% Output %
%%%%%%%%%%
case 3
sys = mdlOutputs(t,x,u);
otherwise
DAStudio.error('Simulink:blocks:unhandledFlag', num2str(flag));
end
% end limintm
%
%=============================================================================
% mdlInitializeSizes
% Return the sizes, initial conditions, and sample times for the S-function.
%=============================================================================
%
function [sys,x0,str,ts,simStateCompliance] = mdlInitializeSizes(lb,ub,xi)
sizes = simsizes;
sizes.NumContStates = 1;%1个连续状态,即积分状态
sizes.NumDiscStates = 0;
sizes.NumOutputs = 1;
sizes.NumInputs = 1;
sizes.DirFeedthrough = 0;
sizes.NumSampleTimes = 1;
sys = simsizes(sizes);
str = [];
x0 = xi; %积分状态初始条件‘
ts = [0 0]; % sample time: [period, offset]
% speicfy that the simState for this s-function is same as the default
simStateCompliance = 'DefaultSimState';
% end mdlInitializeSizes
%
%=============================================================================
% mdlDerivatives
% Compute derivatives for continuous states.
%=============================================================================
%
function sys = mdlDerivatives(t,x,u,lb,ub)
if (x <= lb & u < 0) | (x>= ub & u>0 )
sys = 0;
else
sys = u;
end
% end mdlDerivatives
%
%=============================================================================
% mdlOutputs
% Return the output vector for the S-function
%=============================================================================
%
function sys = mdlOutputs(t,x,u)
sys = x;
% end mdlOutputs
参考:
《基于MATLAB/Simulink系统仿真权威指南》