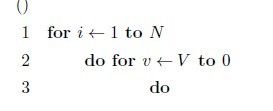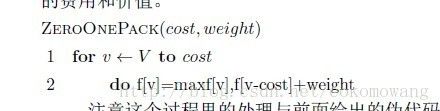- c语言输入两个字符串 按字典数序比较大小,算法学习笔记(一)C++排序函数、映射技巧与字典树...
Nature自然科研
c语言输入两个字符串按字典数序比较大小
1.头文件algorithm中有函数sort()用于排序,参数为:排序起始地址,排序结束地址,排序规则(返回bool型)例如,要将array[]={5,7,1,2,9}升序排列,则使用:boolcmp(inta,intb);intmain(){intarray[]={5,7,1,2,9};sort(array,array+5,cmp);for(inti=0;icoutb)returnfalse;e
- 邓俊辉数据结构与算法学习笔记-第五章
xiaodidadada
数据结构与算法
文章目录树aa1树a2应用a3有根树a4有序树a5路径a6连通图无环图a7深度层次b在计算机中表示b1树的表示b2父节点b3孩子节点b4父亲孩子表示法b5长子兄弟表示法c二叉树c1二叉树概述c2真二叉树c3描述多叉树d二叉树d1BinNode类d2BinNode接口d3BinTree类d4高度更新d5节点插入e相关算法e1-1先序遍历转化策略e1-2遍历规则e1-3递归实现e1-4迭代实现e1-5
- 算法学习笔记-复杂度分析上
胖琪的升级之路
如何分析、统计算法的执行效率和资源消耗为什么需要复杂度分析首先我们很多程序都可以通过统计,监控等方式帮助我们得到程序执行的时间与占用的内存大小。但是这些统计方法有很大的局限性。测试结果非常依赖测试环境。不同的测试机器,同样的代码执行效率就不同。测试结果数受数据规模的影响很大。数据规模大,我们的代码执行效率低。测试结果不能真正的反应我们的内容大O复杂度表示法我们假设一行代码执行一次的时间是unit_
- 不错链接整理
xushuanglu_csdn
提升学习开源
不错链接整理算法https://github.com/MisterBooo/LeetCodeAnimation手把手撕LeetCode题目,扒各种算法套路的裤子https://github.com/labuladong/fucking-algorithm算法学习笔记https://github.com/nonstriater/Learn-Algorithms常用数据结构及其算法的Java实现,包括
- 数据结构与算法学习笔记(训练营三)-经典面试四
剑侠李逍遥
给你一个字符串类型的数组arr,譬如:String[]arr={"b\st","d\","a\d\e","a\b\c"};把这些路径中蕴含的目录结构给打印出来,子目录直接列在父目录下面,并比父目录向右进两格,就像这样:abcdebcstd同一级的需要按字母顺序排列不能乱。利用前缀树,让后深度优先遍历/***给你一个字符串类型的数组arr,譬如:*String[]arr={"b\st","d\","
- 机器学习-近邻KNN算法学习笔记
不会敲代码的陈序员
机器学习算法人工智能
目录一、算法定义KNN算法性能:欠拟合和过拟合KNN算法优缺点二、算法原理算法通俗解释算法的公式欧氏距离曼哈顿距离三、算法实现与应用模型搭建思路KNN算法模型源码代码运行效果图四、总结一、算法定义K最近邻(K-NearestNeighbors,KNN)算法是一种用于分类和回归的监督学习算法。KNN算法的主要思想可以简单概括如下:训练阶段:在训练阶段,KNN算法将所有的训练样本和它们对应的标签存储在
- 算法学习笔记 4-3 深搜(DFS)与广搜(BFS):初识问题状态空间 与 LeetCode真题(Java)
小成同学_
数据结构与算法算法leetcodedfsbfsjava
喜欢该类型文章可以给博主点个关注,博主会持续输出此类型的文章,知识点很全面,再加上LeetCode的真题练习,每一个LeetCode题解我都写了详细注释,比较适合新手入门数据结构与算法,后续也会更新进阶的文章。课件参考—开课吧《门徒计划》4-3深搜(DFS)与广搜(BFS):初识问题状态空间搜索的核心概念首先给大家拓展一个概念,这个概念就是我们学习搜索算法中非常重要的一环:这个问题求解树是一个抽象
- 【小赛1】蓝桥杯双周赛第5场(小白)思路回顾
清风莫追
愚公搬算法蓝桥杯职场和发展python算法
我的成绩:小白(5/6)完稿时间:2024-2-13比赛地址:https://www.lanqiao.cn/oj-contest/newbie-5/相关资料:1、出题人题解:“蓝桥杯双周赛·第5次强者挑战赛/小白入门赛”出题人题解-知乎(zhihu.com)2、矩阵快速幂:算法学习笔记(4):快速幂-知乎(zhihu.com)讲得挺好的,从快速幂到矩阵快速幂,以及在求解递推式中的应用。3、矩阵乘法
- P3870 [TJOI2009] 开关
Fool256353
算法
网址如下:P3870[TJOI2009]开关-洛谷|计算机科学教育新生态(luogu.com.cn)看C艹书看不下去,就到洛谷上随机抽一道题做一道线段树的问题实际上,关于线段树的知识是我现学的(我树的知识都不知道,乐)总结来说,比较重要的就是“懒标记”,加上传值和读取以及构建树的相应操作算法学习网址如下:算法学习笔记(14):线段树-知乎(zhihu.com)第一次用,有点不熟悉,在读取的时候忘记
- Java基础篇1-二分查找与排序算法学习笔记
探索者7号
Java面试篇java
Java基础篇1-二分查找算法与排序算法1.二分查找1.1什么是二分查找?1.2二分查找代码编写1.3获取间索引时,如何避免整数溢出1.3二分查找其他考法2.排序算法2.0Comparable接口介绍2.1冒泡排序2.1.1图解冒泡排序(写代码)2.1.2冒泡排序代码实现2.1.3冒泡排序代码优化2.1.4冒泡排序总结(以升序为例)2.2选择排序(写代码)2.2.1图解选择排序2.2.2选择排序代
- 【分布式】雪花算法学习笔记
少写代码少看论文多多睡觉
Java全栈开发进阶分布式分布式算法学习
雪花算法学习笔记来源https://pdai.tech/md/algorithm/alg-domain-id-snowflake.html概述雪花算法是推特开源的分布式ID生成算法,以划分命名空间的方式将64位分割成多个部分,每一个部分代表不同的含义,这种就是将64位划分成不同的段,每一个段代表不同的涵义时间戳+机器ID+序列数结构第一位占用一个bit值始终为0,可以看作符号位不可使用第二位开始的
- AcWing算法学习笔记:数据结构(单链表 + 双链表 + 栈 + 队列 +单调栈 + 单调队列 + KMP + Trie + 并查集 + 堆 + 哈希表)
一只可爱的小猴子
算法数据结构学习
数据结构一、单链表⭐二、双链表⭐三、栈①模拟栈⭐②表达式求值(还没写)四、模拟队列五、单调栈⭐六、单调队列(滑动窗口)⭐七、KMP字符串⭐⭐八、Trie①Trie字符串统计⭐②最大异或对⭐九、并查集①合并集合②食物链十、堆①堆排序②模拟堆(还没写)十一、哈希表①模拟散列表②字符串哈希一、单链表⭐算法时间复杂度插入删除节点0(1)查询节点0(n)代码#include#include#includeu
- AcWing算法学习笔记:搜索与图论1(DFS + BFS + 树与图的深度优先遍历 + 树与图的广度优先遍历 + 拓扑排序)
一只可爱的小猴子
深度优先算法学习
搜索与图论一、DFS①排列数字②n-皇后问题(还没写)二、BFS①走迷宫②八数码(还没写)三、树与图的深度优先遍历(树的重心)四、树与图的广度优先遍历(图中点的层次)五、有向图的拓扑序列比较空间特点数据结构DFS0(h)第一次搜到的答案不具有最短性stackBFS0(2^h)第一次搜索到的答案一定是最短路queue一、DFS①排列数字算法两个重要概念:回溯和剪枝想好搜索顺序,构建一颗搜索树回溯时一
- AcWing算法学习笔记:贪心(区间问题 + Huffman树 + 排序不等式 + 绝对值不等式 + 推公式)
一只可爱的小猴子
算法学习笔记
贪心一、区间问题①区间选点②最大不相交区间数量③区间分组④区间覆盖二、Huffman树(合并果子)三、排序不等式(排队打水)四、绝对值不等式(货仓选址)五、推公式(耍杂技的牛)一、区间问题①区间选点算法将所有区间的右端点从小到大排序遍历所有的区间若该区间内没有点(左端点大于标记值),则将该区间的右端点设为新的标记值,并且点数加一若这个区间有点,则不处理,跳过该区间代码#include#includ
- AcWing算法学习笔记:基础算法(快速排序 + 归并排序 + 二分 + 高精度 +前缀和差分 + 双指针算法 + 位运算 + 离散化 + 区间和并)
一只可爱的小猴子
算法学习笔记
基础算法一、快速排序①快速排序⭐②第k个数二、归并排序①归并排序②逆序对的数量⭐三、二分①数的范围⭐②数的三次方根⭐四、高精度①高精度加法②高精度减法③高精度乘法④高精度除法五、前缀和差分①前缀和②子矩阵的和③差分④差分矩阵六、双指针算法①最长连续不重复子序列②数组元素的目标和③判断子序列七、位运算(二进制数中1的个数)⭐八、离散化(区间和)⭐九、区间合并一、快速排序①快速排序⭐算法至于关键步骤第
- 数据结构与算法学习笔记(训练营三)-经典面试七
剑侠李逍遥
给定一个无序数组arr,如果只能再一个子数组上排序,返回如果让arr整体有序,需要排序的最短子数组长度。/***给定一个无序数组arr,如果只能再一个子数组上排序,*返回如果让arr整体有序,需要排序的最短子数组长度。*/publicclassMimSubArrayLen{publicstaticintminSubArrayLen(int[]arr){if(arr==null||arr.lengt
- 【精华文章】戊子仲秋的编程学习笔记汇总
戊子仲秋
精华文章学习笔记
文章目录戊子仲秋的学习笔记分享算法学习后端必备知识,打牢基础操作系统Golang学习Linux学习C++学习C语言学习C语言初阶C语言进阶戊子仲秋的学习笔记分享算法学习算法学习笔记汇总后端必备知识,打牢基础操作系统进程管理理解进程、线程、协程I/O多路复用理解I/O多路复用Golang学习Golang基本语法学习Linux学习环境搭建手把手带你用云服务器搭建Linux环境Linux常见指令与权限理
- 【精华文章】戊子仲秋的算法学习笔记汇总
戊子仲秋
精华文章算法学习笔记
文章目录前言通用基础算法集合蓝桥杯备赛算法特训算法学习方法前言我的算法学习之旅,持续更新中通用基础算法集合二分查找二分查找模板:二分原来这么简单二分题目合集:LeetCode上六道经典的二分题目排序算法快速排序模板:双指针快排模板归并排序模板:归并模板堆排序模板:向下调整建堆(到时候专门总结一下)前缀与差分前缀和差分模板:一维、二维的前缀差分单调队列与单调栈单调队列与单调栈模板:维护单调性的思想树
- 【图论】网络流
Texcavator
图论图论网络算法
网络流目前只整理模板,学习的话这篇博客可能不太适合代码参考下方博客,加了一些自己的注释算法学习笔记(28):网络流究级的最大流算法:ISAP与HLPPFF和EK仅用作理解代码,赛时请使用Dinic或ISAP下文建图方式都基于链式前向星,请注意,cnt必须从1开始!!!!voidadd(intu,intv,intval){cnt++;node[cnt].to=v;node[cnt].w=val;no
- 理论学习-C/C++编程-算法学习笔记
用户昵称100
C/C++编程理论指导算法学习c++链表
TOC读《大话数据结构》链表 初看链表程序,就是把指针包装成结构体,前后链接起来。觉得道理浅显易懂,但是自己写又很难写好,只能去copy。明显自己没有学到精髓。 后来,也许是看的多了。不自觉意识到写链表需要提炼的核心要点。帮助写好链表: ①,注意插入的位置。上图“将S插入P之后”,所以在四条语句中都只应用了S和P节点,P节点作为唯一绝对位置,其他节点也只是应用P->next索引。对于“删除节点P”
- 工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(三)——逆运动学P2
Mist_Orz
机器人MATLAB机器人matlab机器人运动学运动学逆解雅克比
文章目录建立DH模型机器人正运动学机器人逆运动学△求θ1\theta_1θ1、θ2\theta_2θ2、θ3\theta_3θ3△代数解求θ4\theta_4θ4、θ5\theta_5θ5、θ6\theta_6θ6○求解θ4\theta_4θ4○求解θ5\theta_5θ5○求解θ6\theta_6θ6△三轴相交的Pieper解法△机器人逆运动学多解的判断机器人雅可比矩阵CSDN提示我字数太多,一
- 工业机器人运动学与Matlab正逆解算法学习笔记(用心总结一文全会)(二)——逆运动学P1
Mist_Orz
机器人MATLABmatlab机器人机器人运动学运动学逆解
文章目录建立DH模型机器人正运动学机器人逆运动学※代数解、几何解,解析解(封闭解)、数值解的含义与联系△代数解求θ1\theta_1θ1、θ2\theta_2θ2、θ3\theta_3θ3※参考资料※关于为何使用atan2()函数求解○求解θ1\theta_1θ1○求解θ3\theta_3θ3○求解θ2\theta_2θ2·机器人学导论的方法(失败的尝试)·参考的文章中的方法(失败的尝试)·一个大
- 算法基础学习笔记——⑤离散化\区间和并
命运之光
#算法基础学习算法
✨博主:命运之光✨专栏:算法基础学习目录✨简述特指整数离散化离散化模板:✨区间和并区间和并模板:前言:算法学习笔记记录日常分享,需要的看哈O(∩_∩)O,感谢大家的支持!✨简述离散化是一种辅助解决问题的操作,当问题中涉及的数据范围非常大,但是实际使用到的数据是比较少的。并且问题的求解是和它范围里的其它数据有关系的,那么可以将这些可能使用到的数据放到一起,排序去重,就将它们映射到了一个新的较小的范围
- 全覆盖规划算法学习笔记-------
大风吹~~~~~
算法学习笔记
ROS全覆盖规划算法通过对比提供的ROS全覆盖规划算法:确定BoustrophedonPlanner和Grid-basedLocalEnergyMinimizationPlanner具备过程应用价值,这里选择后者进行重点研究。参考:官网ipa_room_exploration-ROSWikiIndoorCoveragePathPlanning:Survey,Implementation,Analy
- 数据结构与算法学习笔记(训练营一第三节)---kmp
剑侠李逍遥
KMP(O(N))流程定义两个变量x,y分别表示在原始串str中的位置和匹配串match中的位置。先生成需要匹配的字符串的next数组,next数组记录了当前元素的最长匹配前缀的和后缀的长度,并且也表示如果某一次没有匹配上,那么y需要跳到的位置(最长前缀的下一个元素就是需要继续比较的下一个位置)。同时比较x,y位置的字符是否相等:1.若相等则x,y同时加一向后继续比较。2.若不相等,判断此时该位置
- Matlab智能优化算法学习笔记(一)——粒子群算法、模拟退火算法、遗传算法、蚁群算法
Mist_Orz
MATLABmatlab粒子群算法
文章目录粒子群算法△matlab工具箱粒子群函数○代码○○手搓代码实现粒子群优化2个变量(xy)的粒子群优化尝试·定义函数·绘制网格图(用来可视化过程)·参数初始化,绘制粒子初始位置·开始迭代过程并绘图·获取结果并绘图·运行结果遗传算法△遗传算法概念最近在做一些机器人位姿优化方面的东西,学习了一下关于智能优化算法方面的内容,于是在这里整理一下。最近时间比较紧张,就不写太详细了❤2023.12.12
- 3万字数据结构与算法学习笔记+知识点总结
搬砖成就梦想
c++语法算法c++知识总结学习笔记算法
文章目录数据结构与算法排序排序算法常见排序算法复杂度冒泡排序(BubbleSort)选择排序(SelectionSort)插入排序(InsertionSort)希尔排序(ShellSort)堆排序(HeapSort)归并排序(MergeSort)快速排序(QuickSort)查找二分查找lower_boundupper_bound分治与递归逆序对数大数相加大数相乘贪婪算法动态规划背包问题找零钱问题
- union-find算法
楠风道长
算法数据结构
并查集,即能进行合并(union)与查询(find)的一种数据结构。用来快速判断两个元素的连通性。union-find算法学习笔记并查集(union-find)算法详解例如:A-F,B-C,Z-H,C-F...一对字母表示两地之间的航班,判断是否可以坐飞机从某地到达另一个地方;也可以表示电子通路,判断两个节点是否通电;或者判断两个人之间是否有某种联系......在某些问题中,可能要处理数十亿对数据
- 类欧几里得算法学习笔记
Infinite_Jerry
数论算法学习
类欧几里得算法是欧几里得算法的拓展.这里介绍万能欧几里得算法,他适用性广泛,实现简单,相信你一下就能学会.模型万能欧几里得算法的使用场景为:在一个平面直角坐标系中,有一条直线y=px+rqy=\dfrac{px+r}qy=qpx+r,当其碰到一条横线时执行UUU操作,碰到一条竖线时执行RRR操作.(特别的,当同时碰到定义为先执行UUU).操作必须满足结合律,交换律不需要有.我们定义两个操作s,ts
- 扩展欧几里得算法学习笔记
IImmkk
学习笔记
扩展欧几里得算法:前言:学了两周数据结构发现数论图论忘光了,所以回来补一下,顺便写下笔记。前置需要:欧几里得算法,裴蜀定理,脑子欧几里得算法:即辗转相除法,gcd(a,b)=gcd(b,a mod b)\gcd(a,b)=\gcd(b,a\bmodb)gcd(a,b)=gcd(b,amodb)裴蜀定理:若a,ba,ba,b是整数,且gcd(a,b)=d\gcd(a,b)=dgcd(a,b)=
- 统一思想认识
永夜-极光
思想
1.统一思想认识的基础,才能有的放矢
原因:
总有一种描述事物的方式最贴近本质,最容易让人理解.
如何让教育更轻松,在于找到最适合学生的方式.
难点在于,如何模拟对方的思维基础选择合适的方式. &
- Joda Time使用笔记
bylijinnan
javajoda time
Joda Time的介绍可以参考这篇文章:
http://www.ibm.com/developerworks/cn/java/j-jodatime.html
工作中也常常用到Joda Time,为了避免每次使用都查API,记录一下常用的用法:
/**
* DateTime变化(增减)
*/
@Tes
- FileUtils API
eksliang
FileUtilsFileUtils API
转载请出自出处:http://eksliang.iteye.com/blog/2217374 一、概述
这是一个Java操作文件的常用库,是Apache对java的IO包的封装,这里面有两个非常核心的类FilenameUtils跟FileUtils,其中FilenameUtils是对文件名操作的封装;FileUtils是文件封装,开发中对文件的操作,几乎都可以在这个框架里面找到。 非常的好用。
- 各种新兴技术
不懂事的小屁孩
技术
1:gradle Gradle 是以 Groovy 语言为基础,面向Java应用为主。基于DSL(领域特定语言)语法的自动化构建工具。
现在构建系统常用到maven工具,现在有更容易上手的gradle,
搭建java环境:
http://www.ibm.com/developerworks/cn/opensource/os-cn-gradle/
搭建android环境:
http://m
- tomcat6的https双向认证
酷的飞上天空
tomcat6
1.生成服务器端证书
keytool -genkey -keyalg RSA -dname "cn=localhost,ou=sango,o=none,l=china,st=beijing,c=cn" -alias server -keypass password -keystore server.jks -storepass password -validity 36
- 托管虚拟桌面市场势不可挡
蓝儿唯美
用户还需要冗余的数据中心,dinCloud的高级副总裁兼首席营销官Ali Din指出。该公司转售一个MSP可以让用户登录并管理和提供服务的用于DaaS的云自动化控制台,提供服务或者MSP也可以自己来控制。
在某些情况下,MSP会在dinCloud的云服务上进行服务分层,如监控和补丁管理。
MSP的利润空间将根据其参与的程度而有所不同,Din说。
“我们有一些合作伙伴负责将我们推荐给客户作为个
- spring学习——xml文件的配置
a-john
spring
在Spring的学习中,对于其xml文件的配置是必不可少的。在Spring的多种装配Bean的方式中,采用XML配置也是最常见的。以下是一个简单的XML配置文件:
<?xml version="1.0" encoding="UTF-8"?>
<beans xmlns="http://www.springframework.or
- HDU 4342 History repeat itself 模拟
aijuans
模拟
来源:http://acm.hdu.edu.cn/showproblem.php?pid=4342
题意:首先让求第几个非平方数,然后求从1到该数之间的每个sqrt(i)的下取整的和。
思路:一个简单的模拟题目,但是由于数据范围大,需要用__int64。我们可以首先把平方数筛选出来,假如让求第n个非平方数的话,看n前面有多少个平方数,假设有x个,则第n个非平方数就是n+x。注意两种特殊情况,即
- java中最常用jar包的用途
asia007
java
java中最常用jar包的用途
jar包用途axis.jarSOAP引擎包commons-discovery-0.2.jar用来发现、查找和实现可插入式接口,提供一些一般类实例化、单件的生命周期管理的常用方法.jaxrpc.jarAxis运行所需要的组件包saaj.jar创建到端点的点到点连接的方法、创建并处理SOAP消息和附件的方法,以及接收和处理SOAP错误的方法. w
- ajax获取Struts框架中的json编码异常和Struts中的主控制器异常的解决办法
百合不是茶
jsjson编码返回异常
一:ajax获取自定义Struts框架中的json编码 出现以下 问题:
1,强制flush输出 json编码打印在首页
2, 不强制flush js会解析json 打印出来的是错误的jsp页面 却没有跳转到错误页面
3, ajax中的dataType的json 改为text 会
- JUnit使用的设计模式
bijian1013
java设计模式JUnit
JUnit源代码涉及使用了大量设计模式
1、模板方法模式(Template Method)
定义一个操作中的算法骨架,而将一些步骤延伸到子类中去,使得子类可以不改变一个算法的结构,即可重新定义该算法的某些特定步骤。这里需要复用的是算法的结构,也就是步骤,而步骤的实现可以在子类中完成。
- Linux常用命令(摘录)
sunjing
crondchkconfig
chkconfig --list 查看linux所有服务
chkconfig --add servicename 添加linux服务
netstat -apn | grep 8080 查看端口占用
env 查看所有环境变量
echo $JAVA_HOME 查看JAVA_HOME环境变量
安装编译器
yum install -y gcc
- 【Hadoop一】Hadoop伪集群环境搭建
bit1129
hadoop
结合网上多份文档,不断反复的修正hadoop启动和运行过程中出现的问题,终于把Hadoop2.5.2伪分布式安装起来,跑通了wordcount例子。Hadoop的安装复杂性的体现之一是,Hadoop的安装文档非常多,但是能一个文档走下来的少之又少,尤其是Hadoop不同版本的配置差异非常的大。Hadoop2.5.2于前两天发布,但是它的配置跟2.5.0,2.5.1没有分别。 &nb
- Anychart图表系列五之事件监听
白糖_
chart
创建图表事件监听非常简单:首先是通过addEventListener('监听类型',js监听方法)添加事件监听,然后在js监听方法中定义具体监听逻辑。
以钻取操作为例,当用户点击图表某一个point的时候弹出point的name和value,代码如下:
<script>
//创建AnyChart
var chart = new AnyChart();
//添加钻取操作&quo
- Web前端相关段子
braveCS
web前端
Web标准:结构、样式和行为分离
使用语义化标签
0)标签的语义:使用有良好语义的标签,能够很好地实现自我解释,方便搜索引擎理解网页结构,抓取重要内容。去样式后也会根据浏览器的默认样式很好的组织网页内容,具有很好的可读性,从而实现对特殊终端的兼容。
1)div和span是没有语义的:只是分别用作块级元素和行内元素的区域分隔符。当页面内标签无法满足设计需求时,才会适当添加div
- 编程之美-24点游戏
bylijinnan
编程之美
import java.util.ArrayList;
import java.util.Arrays;
import java.util.HashSet;
import java.util.List;
import java.util.Random;
import java.util.Set;
public class PointGame {
/**编程之美
- 主页面子页面传值总结
chengxuyuancsdn
总结
1、showModalDialog
returnValue是javascript中html的window对象的属性,目的是返回窗口值,当用window.showModalDialog函数打开一个IE的模式窗口时,用于返回窗口的值
主界面
var sonValue=window.showModalDialog("son.jsp");
子界面
window.retu
- [网络与经济]互联网+的含义
comsci
互联网+
互联网+后面是一个人的名字 = 网络控制系统
互联网+你的名字 = 网络个人数据库
每日提示:如果人觉得不舒服,千万不要外出到处走动,就呆在床上,玩玩手游,更不能够去开车,现在交通状况不
- oracle 创建视图 with check option
daizj
视图vieworalce
我们来看下面的例子:
create or replace view testview
as
select empno,ename from emp where ename like ‘M%’
with check option;
这里我们创建了一个视图,并使用了with check option来限制了视图。 然后我们来看一下视图包含的结果:
select * from testv
- ToastPlugin插件在cordova3.3下使用
dibov
Cordova
自己开发的Todos应用,想实现“
再按一次返回键退出程序 ”的功能,采用网上的ToastPlugins插件,发现代码或文章基本都是老版本,运行问题比较多。折腾了好久才弄好。下面吧基于cordova3.3下的ToastPlugins相关代码共享。
ToastPlugin.java
package&nbs
- C语言22个系统函数
dcj3sjt126com
cfunction
C语言系统函数一、数学函数下列函数存放在math.h头文件中Double floor(double num) 求出不大于num的最大数。Double fmod(x, y) 求整数x/y的余数。Double frexp(num, exp); double num; int *exp; 将num分为数字部分(尾数)x和 以2位的指数部分n,即num=x*2n,指数n存放在exp指向的变量中,返回x。D
- 开发一个类的流程
dcj3sjt126com
开发
本人近日根据自己的开发经验总结了一个类的开发流程。这个流程适用于单独开发的构件,并不适用于对一个项目中的系统对象开发。开发出的类可以存入私人类库,供以后复用。
以下是开发流程:
1. 明确类的功能,抽象出类的大概结构
2. 初步设想类的接口
3. 类名设计(驼峰式命名)
4. 属性设置(权限设置)
判断某些变量是否有必要作为成员属
- java 并发
shuizhaosi888
java 并发
能够写出高伸缩性的并发是一门艺术
在JAVA SE5中新增了3个包
java.util.concurrent
java.util.concurrent.atomic
java.util.concurrent.locks
在java的内存模型中,类的实例字段、静态字段和构成数组的对象元素都会被多个线程所共享,局部变量与方法参数都是线程私有的,不会被共享。
- Spring Security(11)——匿名认证
234390216
Spring SecurityROLE_ANNOYMOUS匿名
匿名认证
目录
1.1 配置
1.2 AuthenticationTrustResolver
对于匿名访问的用户,Spring Security支持为其建立一个匿名的AnonymousAuthenticat
- NODEJS项目实践0.2[ express,ajax通信...]
逐行分析JS源代码
Ajaxnodejsexpress
一、前言
通过上节学习,我们已经 ubuntu系统搭建了一个可以访问的nodejs系统,并做了nginx转发。本节原要做web端服务 及 mongodb的存取,但写着写着,web端就
- 在Struts2 的Action中怎样获取表单提交上来的多个checkbox的值
lhbthanks
javahtmlstrutscheckbox
第一种方法:获取结果String类型
在 Action 中获得的是一个 String 型数据,每一个被选中的 checkbox 的 value 被拼接在一起,每个值之间以逗号隔开(,)。
所以在 Action 中定义一个跟 checkbox 的 name 同名的属性来接收这些被选中的 checkbox 的 value 即可。
以下是实现的代码:
前台 HTML 代码:
- 003.Kafka基本概念
nweiren
hadoopkafka
Kafka基本概念:Topic、Partition、Message、Producer、Broker、Consumer。 Topic: 消息源(Message)的分类。 Partition: Topic物理上的分组,一
- Linux环境下安装JDK
roadrunners
jdklinux
1、准备工作
创建JDK的安装目录:
mkdir -p /usr/java/
下载JDK,找到适合自己系统的JDK版本进行下载:
http://www.oracle.com/technetwork/java/javase/downloads/index.html
把JDK安装包下载到/usr/java/目录,然后进行解压:
tar -zxvf jre-7
- Linux忘记root密码的解决思路
tomcat_oracle
linux
1:使用同版本的linux启动系统,chroot到忘记密码的根分区passwd改密码 2:grub启动菜单中加入init=/bin/bash进入系统,不过这时挂载的是只读分区。根据系统的分区情况进一步判断. 3: grub启动菜单中加入 single以单用户进入系统. 4:用以上方法mount到根分区把/etc/passwd中的root密码去除 例如: ro
- 跨浏览器 HTML5 postMessage 方法以及 message 事件模拟实现
xueyou
jsonpjquery框架UIhtml5
postMessage 是 HTML5 新方法,它可以实现跨域窗口之间通讯。到目前为止,只有 IE8+, Firefox 3, Opera 9, Chrome 3和 Safari 4 支持,而本篇文章主要讲述 postMessage 方法与 message 事件跨浏览器实现。postMessage 方法 JSONP 技术不一样,前者是前端擅长跨域文档数据即时通讯,后者擅长针对跨域服务端数据通讯,p