信号与系统实用总结
信号与系统是个比较抽象的课,因为它是用数学建模的方法去分析电路。
那么,我们把电路的现象结合信号与系统的理论指导,就会发现柳暗花明又一村。
1、什么是信号?什么是噪声?
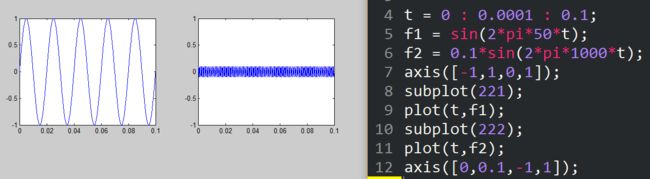
比如,我们现在要用ADC采集50Hz的市电,发现如下图所示的波形。
没错,出来的波形并不是我们想要的光滑的50Hz正弦波,而是有一点奇葩的波形。
经过分析得到,奇葩的波形,是由50Hz正弦波和1KHz的正弦波叠加而成,但是1KHz的正弦波并不是我们想要的东西。
综上所述,你想要的东西就是信号(50Hz),不想要的东西(1KHz)就是噪声。当然,前提是你要清楚你想要的东西是什么。
BTW,信号不仅仅包含电信号,也包含声音、光、热、力等等。
2、什么是系统?
LM324这种运放,就是一个系统。我们不能知道它的内部构造,但是我们可以搭个电路,从外部去测量它的性能。
这就是信号与系统,最重要的思想。把系统当成一个黑匣子,测量外部的信号,从而评估系统的特性。
因为,很多时候,我们不需要知道系统的内部构造。
BTW,系统不仅仅包含运放,小到一个电容,大到整个电路板,任何我们想观察的事物,都可以称为系统。
3、什么是激励?什么是响应?
信号与系统最基本的研究方法就是,用信号发生器送信号到电路板,再用示波器去观察输出的波形。
这种操作,也就是送激励到系统,再观察响应。
如果利用信号发生器扫频的功能,再配合示波器,很容易就得到电路板的幅频特性和相频特性。这就非常有助我们去理解这个电路板的性能。
很多时候我们不关心系统的响应,只关心系统的稳定性。
也没那么多时间去扫频,而且扫频并不是十分方便。所以人们想到一个方法,利用一些频率成份特别丰富的激励去测试系统的稳定性(其中一个频率成份使得系统自激,就说明不稳定,如:运放等电路)。
最常用的激励有:冲激函数、窗函数和阶跃函数。
上图分别为冲激函数的时域图和频谱。显然,冲激函数的频谱是无限广,也就是包含无数个频率成分。
但是冲激函数在物理上不无法实现的。所以人们想到用一个精度足够高的窄脉冲代替冲激函数。这个窄脉冲就是窗函数了。
上图分别为窗函数的时域图和频谱。显然,窗函数的频谱也是无限广,但是更容易现实。
如果没法弄到窄函数,那么,在要求不是很高的情况下,用一个简单的开关动作去产生阶跃函数也是可以的。
上图分别为阶跃函数的时域图和频谱。阶跃函数的频谱也是很广的,虽然比不上冲激函数和窗函数。
4、什么是卷积?
卷积是一种积分,既然是积分,就会有先分割再叠加的操作。如下图所示。
那么卷积就是先把输入信号分割成若干个单位冲激信号,再作用于系统函数(即加权),最后再叠加。
把上图中步骤(1)~(5)的阴影部分累加起来,就得到输出信号。如下图所示。
于是,我们得到卷积的计算公式。
一看,发现没有冲激信号啊,其实上面的公式是一个简化后的公式,它把冲激信号隐藏起来了。
先看看冲激信号的筛选性质。如下图所示。
把一个信号分解成若干个冲激信号,再叠加,其实还是原来的信号,所以卷积中仍然使用h(t-τ),
但是t-τ是冲激信号的延时性质遗留下来的,把h(t)延时τ就得到了h(t-τ)。
为什么要把信号延时、平移?
先延时再平移,才让输入信号和系统函数之间有交集,发生作用。否则的话,哪来输出?
前面延时t为变量τ为常量,现在平移τ为变量t为常量。
τ的取值范围是正负无穷,也就是说把h(t)从负无穷平移到正无穷,所以总能使用输入信号和系统函数产生交集,最终得到输出。
为什么要把信号翻转?
跟时间有关。
我们在图上看到的h(t)函数,把t由小到大排列是h(0)、h(1)、h(2)。。。
但是,细想一下哪个时刻最先出现?没错,是h(0),所以才要把信号翻转一下,使得h(0)最先起作用。
所以利用图解法解释卷积时,一上来就把信号反转,让人有点奇怪。
卷积定理揭示了时域和频域之间的关系,是一个非常重要的定理,这里提一下。
5、什么是傅里叶级数?什么是傅里叶变换?
请认真地看《如果看了这篇文章你还不懂傅里叶变换,那就过来掐死我吧》。
这里不再重复。
BTW,一般的数字示波器都有一个FFT的功能,可以看到信号的频谱,这就非常有利于我们分析信号的频率成份。
6、什么是拉普拉斯变换?
在电学里面,拉普拉斯变换只是作为求解微分方程的一种简单方法,属于积分变换法。
拉普拉斯变换可以把复杂的微分方程转化为线性方程。
利用拉普拉斯变换可以求解各种复杂电路的响应,包含各种看起来很高大上、很复杂的运放电路。如下图所示。
但是,这么复杂的计算,可以用仿真工具来完成,如:multisim或者ADS等。
很多人认为拉普拉斯变换没用,其实是仿真工具用了。
熟练使用拉普拉斯变换,有利于理解电路的稳定性、响应,可以提高硬件设计能力。
7、什么是Z变换?
拉普拉斯变换适用于连续信号,但是计算机难以处理连续信号(无数个点)。
把连续信号采样后,再做z变换,所有的计算变成有限个点,这样才能送到计算机中处理。z变换也就是离散信号的拉普拉斯变换。
z变换和拉普拉斯在定义、性质上都是大同小异,这里不再重复。
特别需要指出,z的-1次方,其实就是对应于一个D触发器,可以延时一个时钟周期。
而z的2次方,是超前2个时钟周期,不易于用物理实现,那么,你可以把超前换成滞后(整个电路滞后3拍),就能转化为D触发器了。