2020.5.27 线性规划测试(Lingo实现)
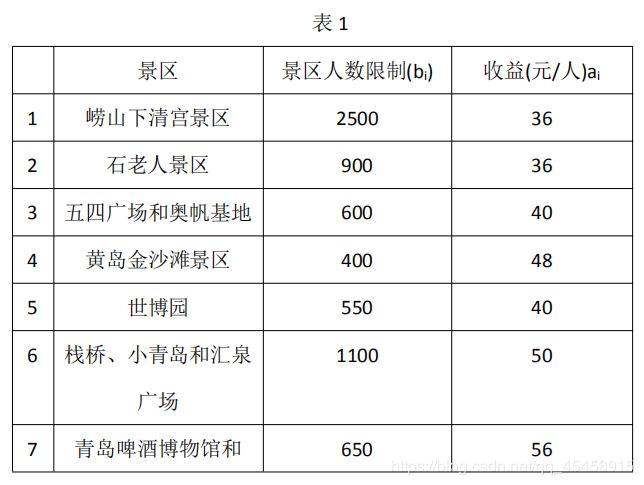
青岛某旅游公司五一长假准备推出旅游两日游套餐。旅游项目选择以下 7 种组合(见表 1):
旅游公司计划在上述 7 种景点组合中选择 3 种组成二日游套餐。 由于疫情期间,为了预防人的聚集,各景点对旅游团人数有一定限制, 每两天该旅行社到各景点组合的人数配额限制,且不同的景点组合每 个游客给旅游公司带来的收益不同(见表 1)。根据公司的条件,公司 计划每两天最多安排 2100 人的旅游计划。
-
如果景点 1 是必选项,且以收益最大为目标,应该推出哪几种二日游套餐,每种套餐各有多少人?
- 旅游期间要配备旅游车。由于疫情期间人与人的间距要求,每辆车最多搭载旅客 26 人,并要求接待旅游人数不低于 2000人。如果在需求车辆数最小的前提下收益最大,应该推出哪几种二日游套餐,每种套餐各多少人?
- 不再把景点 1 作为必选项,考虑到有些景观差异性较小,以及景点距离太大费用较大,因此在设计旅游套餐时增加规定:第2、3、6 这 3 类景区必须且只需选择一个,第 6 和第 7 不能同时选取,第1 和第 4 不能同时选取,并要求总接待人数不低于1200。在这种要求下,按照在车辆最少的前提下收益最高的目标,旅游套餐的选择方案应如何制定?
反思:不算很难的一次测试,但是自己还是拉了胯,总感觉自己想出的模型已经天衣无缝了,一度在怀疑是优化软件的问题,但实际上还是可以优化的,归根结底还是自己太菜了,吸取到的教训就是以后建模能尽量多开变量就不要少开,不要弄那些花里胡哨的化简来减少变量的数量
模型分析:结合下料问题以及学生选课问题这两个模型,不难确定如下变量:
- a[ i ] :景区 i 的收益单价
- b[ i ] :景区 i 的人数限制
- y[ j ] :选择套餐 j 的人数
- w[ j ] :套餐 j 的收益单价
- x[ j ] :套餐 j 需要车的数量(第二问第三问需要用到)
第一问
在读懂题目后不难想到,可以直接暴力枚举出所有的可行方案生成套餐,因为第一问中约束了景区 1 是必选的,那么剩下的 6 个景区内需要选出 2 个,共 C( 6 , 2 ) = 15 种方案,到此为止不难写出第一问的程序了(约束条件直接看代码吧,懒得另写了)
最大收益:264600
sets:
t1/1..7/:a,b;
t2/1..15/:w,y;
endsets
max=@sum(t2:y*w);
@sum(t2:y)<=2100;
y(1)+y(2)+y(3)+y(4)+y(5)<=b(2);
y(1)+y(6)+y(7)+y(8)+y(9)<=b(3);
y(2)+y(6)+y(10)+y(11)+y(12)<=b(4);
y(3)+y(7)+y(10)+y(13)+y(14)<=b(5);
y(4)+y(8)+y(11)+y(13)+y(15)<=b(6);
y(5)+y(9)+y(12)+y(14)+y(15)<=b(7);
@for(t2:@gin(y));
data:
b=2500,900,600,400,550,1100,650;
a=36,36,40,48,40,50,56;
w=112,120,112,122,128,124,116,126,132,124,134,140,126,132,142;
@text()=@table(y);
enddata第二问
第二问的话有两个目标函数,但其实可以分解成两个小问题,因为题目已经标明了两个目标函数的先后顺序了,在第一问的基础上加上约束变量 ![]() 就可以求出最小的车辆数了
就可以求出最小的车辆数了
最小车辆:77
sets:
t1/1..7/:a,b;
t2/1..15/:w,y,x;
endsets
min=@sum(t2:x);
@sum(t2:y)<=2100;
@sum(t2:y)>=2000;
@sum(t2:y)<=b(1);
y(1)+y(2)+y(3)+y(4)+y(5)<=b(2);
y(1)+y(6)+y(7)+y(8)+y(9)<=b(3);
y(2)+y(6)+y(10)+y(11)+y(12)<=b(4);
y(3)+y(7)+y(10)+y(13)+y(14)<=b(5);
y(4)+y(8)+y(11)+y(13)+y(15)<=b(6);
y(5)+y(9)+y(12)+y(14)+y(15)<=b(7);
@for(t2:@gin(y));
@for(t2:@gin(x));
@for(t2:26*x>=y);
data:
b=2500,900,600,400,550,1100,650;
a=36,36,40,48,40,50,56;
w=112,120,112,122,128,124,116,126,132,124,134,140,126,132,142;
@text()=@table(y);
enddata到此已经求出了最小车辆数是 77 辆,接下来利用车辆的约束再求最大收益就好了
最大收益:253760
sets:
t1/1..7/:a,b;
t2/1..15/:w,y,x;
endsets
max=@sum(t2:y*w);
@sum(t2:y)<=2100;
@sum(t2:y)>=2000;
@sum(t2:y)<=b(1);
y(1)+y(2)+y(3)+y(4)+y(5)<=b(2);
y(1)+y(6)+y(7)+y(8)+y(9)<=b(3);
y(2)+y(6)+y(10)+y(11)+y(12)<=b(4);
y(3)+y(7)+y(10)+y(13)+y(14)<=b(5);
y(4)+y(8)+y(11)+y(13)+y(15)<=b(6);
y(5)+y(9)+y(12)+y(14)+y(15)<=b(7);
@for(t2:@gin(y));
@for(t2:@gin(x));
@for(t2:26*x>=y);
@sum(t2:x)=77;
data:
b=2500,900,600,400,550,1100,650;
a=36,36,40,48,40,50,56;
w=112,120,112,122,128,124,116,126,132,124,134,140,126,132,142;
@text()=@table(y);
enddata第三问
第三问其实就是第二问的一个小变形,区别就在于套餐的选择换了一些约束,针对这些约束不难编程求出可行方案以及收益单价,这里用C++实现的
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include
#include 到这里可以求出共有 12 种套餐,且具体的选择方案以及单价都可以求出来,接下来套入第二问的模型中去,就可以直接求出最小车辆,从而求出最大利润了
最小车辆:47
sets:
t1/1..7/:a,b;
t2/1..12/:w,y,x;
endsets
min=@sum(t2:x);
@sum(t2:y)<=2100;
@sum(t2:y)>=1200;
y(1)+y(2)+y(3)+y(4)+y(5)<=b(1);
y(1)+y(2)+y(6)+y(7)+y(8)<=b(2);
y(3)+y(4)+y(9)+y(10)+y(11)<=b(3);
y(6)+y(7)+y(9)+y(10)+y(12)<=b(4);
y(1)+y(3)+y(5)+y(6)+y(8)+y(9)+y(11)+y(12)<=b(5);
y(5)+y(12)<=b(6);
y(2)+y(4)+y(7)+y(8)+y(10)+y(11)<=b(7);
@for(t2:@gin(y));
@for(t2:@gin(x));
@for(t2:26*x>=y);
data:
b=2500,900,600,400,550,1100,650;
a=36,36,40,48,40,50,56;
w=112,128,116,132,126,124,140,132,128,144,136,138;
@text()=@table(y);
enddata最大收益:159692
sets:
t1/1..7/:a,b;
t2/1..12/:w,y,x;
endsets
max=@sum(t2:y*w);
@sum(t2:y)<=2100;
@sum(t2:y)>=1200;
y(1)+y(2)+y(3)+y(4)+y(5)<=b(1);
y(1)+y(2)+y(6)+y(7)+y(8)<=b(2);
y(3)+y(4)+y(9)+y(10)+y(11)<=b(3);
y(6)+y(7)+y(9)+y(10)+y(12)<=b(4);
y(1)+y(3)+y(5)+y(6)+y(8)+y(9)+y(11)+y(12)<=b(5);
y(5)+y(12)<=b(6);
y(2)+y(4)+y(7)+y(8)+y(10)+y(11)<=b(7);
@for(t2:@gin(y));
@for(t2:@gin(x));
@for(t2:26*x>=y);
@sum(t2:x)=47;
data:
b=2500,900,600,400,550,1100,650;
a=36,36,40,48,40,50,56;
w=112,128,116,132,126,124,140,132,128,144,136,138;
@text()=@table(y);
enddata