HDU-2732 Leapin' Lizards(建图+dinic最大流)

HDU-2732 Leapin’ Lizards(建图+dinic最大流)

题目链接：http://acm.hdu.edu.cn/showproblem.php?pid=2732

我的博客：https://acmerszq.cn

题意：

​ 共有T组样例。每组样例的第一行为n和d，n代表图有多少行，d代表蜥蜴最多能跳多远 （距离为曼哈顿距离）。接下来输入两个矩阵，分别代表石柱能承受多少次跳跃和蜥蜴在哪些石柱上 （L代表蜥蜴）。蜥蜴跳出矩阵外就算逃出，要你求有多少蜥蜴不能逃出。

思路：

​ 虽说是道网络流的题，但如果这道题不在网络流专题里我大概不会想到网络流来做。

​ 这道题最主要的是建图。

​ 第一步，我把0设置为源点，1设置为终点。

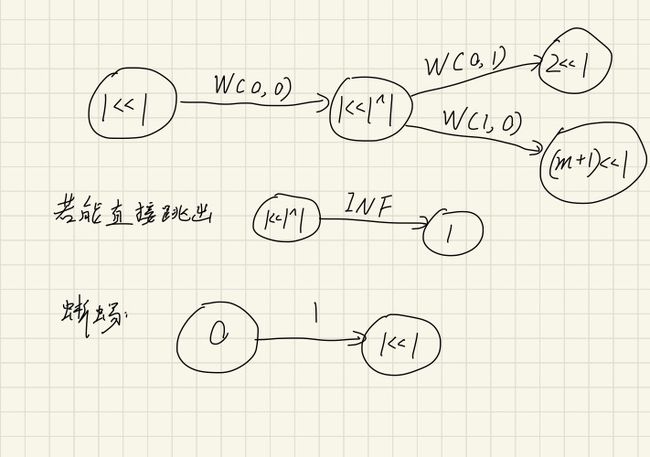
​ 第二步，我想到的是要限制石柱的跳跃次数的话就弄一个石柱入口和一个石柱出口，入口和出口的flow权值设置为跳跃限制次数。然后要把在跳跃距离中并且不为‘0’的石柱建路，路的权值是目标石柱的限制次数。但是如果这个石柱可以直接跳出就加入与终点相连的路径，并且设置权值为INF。

​ 第三步，处理蜥蜴的位置就简单很多了，只要把源点设置为u，蜥蜴位置设置为v，w设置为1即可。

​ 大致的建图示范：

AC代码：

#include 
using namespace std;
const int MAXN = 2010;     //点数的最大值
const int MAXM = 1200010;  //边数的最大值
const int INF = 0x3f3f3f3f;
struct Edge {
    int to, next, cap, flow;
} edge[MAXM];  //注意是 MAXM
int tol;
int head[MAXN];
void init() {
    tol = 2;
    memset(head, -1, sizeof(head));
}
void addedge(int u, int v, int w, int rw = 0) {
    edge[tol].to = v;
    edge[tol].cap = w;
    edge[tol].flow = 0;
    edge[tol].next = head[u];
    head[u] = tol++;
    edge[tol].to = u;
    edge[tol].cap = rw;
    edge[tol].flow = 0;
    edge[tol].next = head[v];
    head[v] = tol++;
}
int Q[MAXN];
int dep[MAXN], cur[MAXN], sta[MAXN];
bool bfs(int s, int t, int n) {
    int front = 0, tail = 0;
    memset(dep, -1, sizeof(dep[0]) * (n + 1));
    dep[s] = 0;
    Q[tail++] = s;
    while (front < tail) {
        int u = Q[front++];
        for (int i = head[u]; i != -1; i = edge[i].next) {
            int v = edge[i].to;
            if (edge[i].cap > edge[i].flow && dep[v] == -1) {
                dep[v] = dep[u] + 1;
                if (v == t) return true;
                Q[tail++] = v;
            }
        }
    }
    return false;
}
int dinic(int s, int t, int n) {
    int maxflow = 0;
    while (bfs(s, t, n)) {
        for (int i = 0; i < n; i++) cur[i] = head[i];
        int u = s, tail = 0;
        while (cur[s] != -1) {
            if (u == t) {
                int tp = INF;
                for (int i = tail - 1; i >= 0; i--) tp = min(tp, edge[sta[i]].cap - edge[sta[i]].flow);
                maxflow += tp;
                for (int i = tail - 1; i >= 0; i--) {
                    edge[sta[i]].flow += tp;
                    edge[sta[i] ^ 1].flow -= tp;
                    if (edge[sta[i]].cap - edge[sta[i]].flow == 0) tail = i;
                }
                u = edge[sta[tail] ^ 1].to;
            } else if (cur[u] != -1 && edge[cur[u]].cap > edge[cur[u]].flow && dep[u] + 1 == dep[edge[cur[u]].to]) {
                sta[tail++] = cur[u];
                u = edge[cur[u]].to;
            } else {
                while (u != s && cur[u] == -1) u = edge[sta[--tail] ^ 1].to;
                cur[u] = edge[cur[u]].next;
            }
        }
    }
    return maxflow;
}
char maze[50][50];
bool vis[50][50];
void add(int b, int x, int y, int d, int n, int m) {
    vis[x][y] = true;
    if (maze[x - 1][y] != '0' && !vis[x - 1][y]) {
        addedge(b, ((x - 1) * m + y + 1) << 1, maze[x - 1][y] - '0');
        vis[x - 1][y] = true;
    }
    if (maze[x + 1][y] != '0' && !vis[x + 1][y]) {
        addedge(b, ((x + 1) * m + y + 1) << 1, maze[x + 1][y] - '0');
        vis[x + 1][y] = true;
    }
    if (maze[x][y - 1] != '0' && !vis[x][y - 1]) {
        addedge(b, (x * m + y) << 1, maze[x][y - 1] - '0');
        vis[x][y - 1] = true;
    }
    if (maze[x][y + 1] != '0' && !vis[x][y + 1]) {
        addedge(b, (x * m + y + 2) << 1, maze[x][y + 1] - '0');
        vis[x][y + 1] = true;
    }
    if (d != 1) {
        add(b, x - 1, y, d - 1, n, m);
        add(b, x + 1, y, d - 1, n, m);
        add(b, x, y - 1, d - 1, n, m);
        add(b, x, y + 1, d - 1, n, m);
    }
}
int main() {  //m*n*2+2
    // freopen("RAW/in", "r", stdin);
    // freopen("RAW/out", "w", stdout);
    int T;
    scanf("%d", &T);
    for (int _ = 1; _ <= T; _++) {
        init();
        memset(maze, 0, sizeof(maze));
        printf("Case #%d: ", _);
        int n, d;
        scanf("%d%d", &n, &d);
        for (int i = 0; i < n; i++) {
            scanf("%s", maze[i]);
        }
        int m = strlen(maze[0]);
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < m; j++) {
                int a = (i * m + (j + 1)) << 1;
                int b = a ^ 1;
                int t = maze[i][j] - '0';
                if (maze[i][j] - '0' > 0)
                    addedge(a, b, t);
                else
                    continue;
                if (i < d || j < d || i + d >= n || j + d >= m) {
                    addedge(b, 1, INF);
                    continue;
                }
                memset(vis, 0, sizeof(vis));
                add(b, i, j, d, n, m);
            }
        }
        int sum = 0;
        for (int i = 0; i < n; i++) {
            scanf("%s", maze[i]);
            for (int j = 0; j < m; j++) {
                if (maze[i][j] == 'L') {
                    addedge(0, (i * m + (j + 1)) << 1, 1);
                    sum++;
                }
            }
        }
        int ans = dinic(0, 1, 2 * m * n + 2);
        ans = sum - ans;
        if (ans == 0) {
            printf("no lizard was left behind.\n");
        } else if (ans == 1) {
            printf("1 lizard was left behind.\n");
        } else {
            printf("%d lizards were left behind.\n", ans);
        }
        // printf("%d\n", sum - ans);
    }
    return 0;
}