凸优化学习笔记 1:Convex Sets
个人博客 Glooow ,欢迎各位大驾光临
文章目录
- 1. 凸集
- 2. 常见凸集
- 2.1 凸包(Convec hull)
- 2.2 超平面(Hyperplanes)
- 2.3 半空间(Halfspaces)
- 2.4 多面体(Polyhedra)
- 2.5 欧几里得球与椭球(Euclidean balls and ellipsoids)
- 2.6 范数球(norm balls)
- 2.7 凸锥(Convex cone)
- 2.8 范数锥(norm cone)
- 2.9 半正定锥
- 3. 保凸变换
- 3.1 凸集的交集
- 3.2 仿射变换
- 3.3 投影变换
- 3.4 分式线性函数
1. 凸集
区分两种集合的定义(下面的描述并不是严格的数学语言,领会意思就行了):
- 仿射集(Affine set): x = θ x 1 + ( 1 − θ ) x 2 , θ ∈ R x=\theta x_1 + (1-\theta)x_2,\quad \theta\in\mathbb{R} x=θx1+(1−θ)x2,θ∈R
- 凸集(Convex set): x = θ x 1 + ( 1 − θ ) x 2 , θ ∈ [ 0 , 1 ] x=\theta x_1 + (1-\theta)x_2,\quad \theta\in[0,1] x=θx1+(1−θ)x2,θ∈[0,1]
主要的区别就在于后面 θ \theta θ 的取值范围,简单理解就是说仿射集类似直线,凸集类似线段。
更一般的,仿射集都可以表示为线性方程组的解集,也即 { x ∣ A x = b } \{x|Ax=b\} {x∣Ax=b}
2. 常见凸集
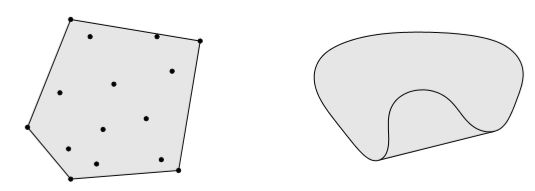
2.1 凸包(Convec hull)
假如集合 S = { x 1 , . . . , x k } S=\{x_1,...,x_k\} S={x1,...,xk},则其凸包可以表示为
{ ∑ i = 1 k θ i x i ∣ ∑ θ i = 1 , θ i ≥ 0 } \left\{\sum_{i=1}^k\theta_i x_i \vert \sum\theta_i=1, \theta_i\ge0\right\} {i=1∑kθixi∣∑θi=1,θi≥0}
2.2 超平面(Hyperplanes)
类比三维空间中的平面,可以有超平面的定义
{ x ∣ a T x = b } ( a ≠ 0 ) \left\{x\vert a^Tx=b\right\}(a\ne0) {x∣aTx=b}(a=0)
其中 a a a 就是该平面的法向量。
2.3 半空间(Halfspaces)
类似的,有半空间定义为
{ x ∣ a T x ≤ b } ( a ≠ 0 ) \left\{x\vert a^Tx\le b\right\}(a\ne0) {x∣aTx≤b}(a=0)
2.4 多面体(Polyhedra)
高维空间中的多面体定义为
{ x ∣ A x ⪯ b , C x = d } \left\{x\vert A x \preceq b, \quad C x=d \right\} {x∣Ax⪯b,Cx=d}
其中 ⪯ \preceq ⪯ 表示对每个元素都作比较。实际上就是求很多个半空间以及半平面的交集,与三维空间是类似的。
2.5 欧几里得球与椭球(Euclidean balls and ellipsoids)
高维空间中的欧几里得球的定义为
B ( x c , r ) = { x ∣ ∥ x − x c ∥ 2 ≤ r } = { x c + r u ∣ ∥ u ∥ 2 ≤ 1 } B\left(x_{c}, r\right)=\left\{x |\left\|x-x_{c}\right\|_{2} \leq r\right\}=\left\{x_{c}+r u |\|u\|_{2} \leq 1\right\} B(xc,r)={x∣∥x−xc∥2≤r}={xc+ru∣∥u∥2≤1}
椭球的定义为
{ x ∣ ( x − x c ) T P − 1 ( x − x c ) ≤ 1 } = { x c + A u ∣ ∥ u ∥ 2 ≤ 1 } \left\{x |\left(x-x_{c}\right)^{T} P^{-1}\left(x-x_{c}\right) \leq 1\right\} = \left\{x_{c}+A u |\|u\|_{2} \leq 1\right\} {x∣(x−xc)TP−1(x−xc)≤1}={xc+Au∣∥u∥2≤1}
其中 P ∈ S + + n P \in \mathbf{S}_{++}^{n} P∈S++n (也即 P P P 为对称正定矩阵)。中间的矩阵 P P P 的作用就相当于在各个特征向量方向上进行了放缩。
Remarks:关于矩阵性质,可以参考我的矩阵论学习笔记,这里复习一个知识点。
- 正规矩阵的定义为满足 A H A = A A H A^HA=AA^H AHA=AAH 的矩阵 A A A 即为正规矩阵,因此对称矩阵、Hermit矩阵、酉矩阵都是正规矩阵。而正规矩阵有什么性质呢?正规矩阵可以对角化,且存在一组正交的特征向量!
- 正定矩阵的定义为满足 x T A x > 0 x^TAx>0 xTAx>0 的矩阵 A A A,实际上也就是说矩阵 A A A 的特征值均大于 0!
- 因此对称正定矩阵的性质有:所有特征向量正交,所有特征值大于 0。
2.6 范数球(norm balls)
范数 ∥ ⋅ ∥ \Vert\cdot\Vert ∥⋅∥ 需要满足以下性质
- ∥ x ∥ ≥ 0 ; ∥ x ∥ = 0 ⟺ x = 0 \Vert x \Vert\ge0;\ \Vert x\Vert=0 \iff x=0 ∥x∥≥0; ∥x∥=0⟺x=0
- ∥ t x ∥ = ∣ t ∣ ∥ x ∥ \|t x\|=|t|\|x\| ∥tx∥=∣t∣∥x∥ for t ∈ R t \in \mathbf{R} t∈R
- ∥ x + y ∥ ≤ ∥ x ∥ + ∥ y ∥ \|x+y\| \leq\|x\|+\|y\| ∥x+y∥≤∥x∥+∥y∥
向量范数如 ∥ x ∥ 0 , ∥ x ∥ 1 , ∥ x ∥ 2 , ∥ x ∥ p , ∥ x ∥ ∞ \Vert x\Vert_0, \Vert x\Vert_1, \Vert x\Vert_2, \Vert x\Vert_p, \Vert x\Vert_\infty ∥x∥0,∥x∥1,∥x∥2,∥x∥p,∥x∥∞
矩阵范数如 ∥ X ∥ 2 , ∥ X ∥ p \Vert X\Vert_2, \Vert X\Vert_p ∥X∥2,∥X∥p
范数球的定义为
{ x ∣ ∥ x − x c ∥ ≤ r } \left\{x |\left\|x-x_{c}\right\| \leq r\right\} {x∣∥x−xc∥≤r}
2.7 凸锥(Convex cone)
我们先来看看锥的定义
- 锥(cone): x ∈ C ⇒ θ x ∈ C , ∀ θ ≥ 0 x\in C\Rightarrow \theta x\in C, \forall \theta\ge0 x∈C⇒θx∈C,∀θ≥0
- 凸锥(Convex cone): x 1 , x 2 ∈ C ⇒ x = θ 1 x 1 + θ 2 x 2 ∈ C , ∀ θ 1 , θ 2 ≥ 0 x_1,x_2\in C \Rightarrow x=\theta_1 x_1+\theta_2 x_2 \in C,\forall \theta_1,\theta_2\ge0 x1,x2∈C⇒x=θ1x1+θ2x2∈C,∀θ1,θ2≥0
注意锥一定包含原点 0。锥不一定是凸的,反例如下,这是一个锥,但不是凸锥
2.8 范数锥(norm cone)
范数锥定义如下
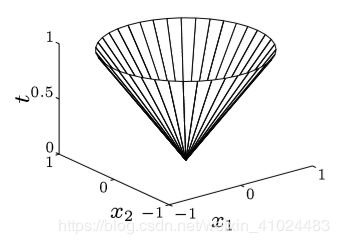
{ ( x , t ) ∣ ∥ x ∥ ≤ t } \{(x, t) |\|x\| \leq t\} {(x,t)∣∥x∥≤t}
也被称为 Ice cream cone。其中欧几里得范数锥被称为二阶锥(second-order cone)
2.9 半正定锥
定义几个符号
- S n \mathbf{S}^{n} Sn 为 n n n 阶对称矩阵
- S + n = { X ∈ S n ∣ X ⪰ 0 } \mathbf{S}_{+}^{n}=\left\{X \in \mathbf{S}^{n} | X \succeq 0\right\} S+n={X∈Sn∣X⪰0} 为对称半正定矩阵,为凸锥
- S + + n = { X ∈ S n ∣ X ≻ 0 } \mathbf{S}_{++}^{n}=\left\{X \in \mathbf{S}^{n} | X \succ 0\right\} S++n={X∈Sn∣X≻0} 为对称正定矩阵
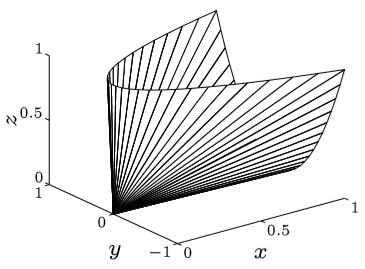
例如给定二阶矩阵
[ x y y z ] ∈ S + 2 \left[\begin{array}{ll} {x} & {y} \\ {y} & {z} \end{array}\right] \in \mathrm{S}_{+}^{2} [xyyz]∈S+2
其坐标满足如下图
3. 保凸变换
上面是一些常见的凸集,对于更复杂的情况,怎么判断是否为凸集呢?
- 根据定义 x 1 , x 2 ∈ C , 0 ≤ θ ≤ 1 ⟹ θ x 1 + ( 1 − θ ) x 2 ∈ C x_{1}, x_{2} \in C, \quad 0 \leq \theta \leq 1 \quad \Longrightarrow \quad \theta x_{1}+(1-\theta) x_{2} \in C x1,x2∈C,0≤θ≤1⟹θx1+(1−θ)x2∈C
- 凸集经过保凸变换以后仍然是凸集,如
- 凸集的交集
- 仿射变换
- 投影变换
- 分式线性映射
3.1 凸集的交集
任意个(可以是无数个)凸集的交集仍然是凸集
例子 1: S = { x ∈ R m ∣ ∣ p ( t ) ∣ ≤ 1 for ∣ t ∣ ≤ π / 3 } S=\left\{x \in \mathbf{R}^{m}|| p(t) | \leq 1 \text { for }|t| \leq \pi / 3\right\} S={x∈Rm∣∣p(t)∣≤1 for ∣t∣≤π/3},其中 p ( t ) = x 1 cos t + x 2 cos 2 t + ⋯ + x m cos m t p(t)=x_{1} \cos t+x_{2} \cos 2 t+\cdots+x_{m} \cos m t p(t)=x1cost+x2cos2t+⋯+xmcosmt
3.2 仿射变换
若映射 f : R n → R m f: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m} f:Rn→Rm 是仿射变换
f ( x ) = A x + b with A ∈ R m × n , b ∈ R m f(x)=A x+b \text { with } A \in \mathbf{R}^{m \times n}, b \in \mathbf{R}^{m} f(x)=Ax+b with A∈Rm×n,b∈Rm
则有
- S ⊆ R n S \subseteq \mathbf{R}^{n} S⊆Rn convex ⟹ f ( S ) = { f ( x ) ∣ x ∈ S } \Longrightarrow f(S)=\{f(x) | x \in S\} ⟹f(S)={f(x)∣x∈S} convex
- C ⊆ R m C \subseteq \mathbf{R}^{m} C⊆Rm convex ⟹ f − 1 ( C ) = { x ∈ R n ∣ f ( x ) ∈ C } \Longrightarrow f^{-1}(C)=\left\{x \in \mathbf{R}^{n} | f(x) \in C\right\} ⟹f−1(C)={x∈Rn∣f(x)∈C} convex
例子 2:双曲锥 { x ∣ x T P x ≤ ( c T x ) 2 , c T x ≥ 0 } ( with P ∈ S + n ) \left\{x | x^{T} P x \leq\left(c^{T} x\right)^{2}, c^{T} x \geq 0\right\}\left(\text { with } P \in \mathbf{S}_{+}^{n}\right) {x∣xTPx≤(cTx)2,cTx≥0}( with P∈S+n),因为其可以转化为二阶锥
例子 3: { x ∣ x 1 A 1 + ⋯ + x m A m ⪯ B } \left\{x | x_{1} A_{1}+\cdots+x_{m} A_{m} \preceq B\right\} {x∣x1A1+⋯+xmAm⪯B}(with A i , P ∈ S p A_i,P\in S^p Ai,P∈Sp)???
3.3 投影变换
投影函数 P : R n + 1 → R n P: \mathbf{R}^{n+1} \rightarrow \mathbf{R}^{n} P:Rn+1→Rn
P ( x , t ) = x / t , dom P = { ( x , t ) ∣ t > 0 } P(x, t)=x / t, \quad \operatorname{dom} P=\{(x, t) | t>0\} P(x,t)=x/t,domP={(x,t)∣t>0}
Proof:略。应用凸集定义
3.4 分式线性函数
分式线性映射 f : R n → R m f: \mathbf{R}^{n} \rightarrow \mathbf{R}^{m} f:Rn→Rm 为
f ( x ) = A x + b c T x + d , dom f = { x ∣ c T x + d > 0 } f(x)=\frac{A x+b}{c^{T} x+d}, \quad \text { dom } f=\left\{x | c^{T} x+d>0\right\} f(x)=cTx+dAx+b, dom f={x∣cTx+d>0}
其可以看作先仿射变换再投影变换。