前缀表达式与后缀表达式求法(栈的应用)
1.前缀、中缀、后缀表达式
中缀表达式即为人们熟悉的数学运算式子写法。而前缀、后缀表达式是为了计算机计算方便的写法。
前缀表达式是一种没有括号的算术表达式,与中缀表达式不同的是,其将运算符写在前面,操作数写在后面。后缀表达式则是将操作数写在前面,运算符写在后面。
前缀表达式又称波兰表达式,后缀表达式又称逆波兰表达式。通过利用栈的特性,我们可以从中缀表达式得到前后缀表达式,轻松的计算出其结果。
我们先写一组表达式,后面就用这组表达式:
中缀:9*8+(14-8/2)*3
前缀:+ * 9 8 * - 14 / 8 2 3 //这里把每一个操作数或运算符用空格分开
后缀:9 8 * 14 8 2 / - 3 * +
如何存储前缀和后缀表达式呢?如果直接用字符串,那么数字之前就会混乱,所以我用了结构体存储:
struct A
{
int a;
char type; //数字为0,符号为1
};
struct Poland //前缀/后缀表达式的存储方式 不用string的原因是,无法从字符串中分开操作数
{
char type; //p前缀 s后缀
int lenth;
A *content;
};
2.中缀表达式转前缀表达式
①初始化两个栈S1,S2,从右往左扫描中缀式。
②遇到操作数:将其压入S2栈。
③遇到括号时:
若是右括号‘)’,将其压入S1栈;
若是左括号‘(’,则依次弹出S1栈的元素,并将其压入S2栈,直至S1栈栈顶元素为右括号‘)’,弹出这个右括号。
④遇到运算符时:
若S1栈为空或者其栈顶元素为右括号‘)’,将其压入S1。
否则,比较运算符和S1栈顶运算符(一定是运算符)的优先级:
若其优先级≥S1栈顶运算符,则将其压入S1;
若小于,则将S1栈顶运算符弹出并压入S2,重新进行步骤④。
⑤重复②③④直到到达中缀式最左边,将S1剩余元素压入S2。最后依次取出S2元素即为前缀表达式。
代码:
/*已知中缀表达式,求前缀表达式*/
Poland infix_to_prefix(string infix)
{
stack s1, s2;
regex p("(\\d+)"); //用于查找数字的正则式
string s = infix;
reverse(s.begin(), s.end()); //求前缀式需要从右往左扫描,为了方便,直接颠倒字符串
string::const_iterator iter = s.begin();
string::const_iterator iter_end = s.end();
while (iter < iter_end)
{
smatch result;
if (iter >= iter_end) //防止迭代器位置超出字符串
break;
if (*iter >= '0'&&*iter <= '9') //遇操作数 这里不能直接用regex_search,必须要确定后面的字符串第一个字符是数字
{
regex_search(iter, iter_end, result, p);
string temp = result[0];
int num = atoi(temp.c_str()); //string转int c_str函数返回当前字符串的首字符地址
A sym1;
sym1.a = num;
sym1.type = 0;
s2.push(sym1);
iter = result[0].second; //别忘了更新迭代器位置,这里second表示查找到的数字在源串中后面部分串的首地址
}
else //遇符号
{
char ope = *iter;
A sym2;
sym2.a = (int)ope;
sym2.type = 1;
label:
if (ope == ')') //遇右括号,直接入栈
{
s1.push(sym2);
}
else if (ope == '(') //遇左括号,将栈内直到右括号之前的元素依次弹出压入S2
{
while (s1.top().a != (int)')')
{
A t = s1.top();
s1.pop();
s2.push(t);
}
//这里让)也出栈
s1.pop();
}
else //其他运算符,如 %/* >= +-
{
if (s1.empty() || (s1.top().a == (int)')'&&s1.top().type == 1)) //若s1为空或其栈顶为),符号入栈s1 或者符号优先级>=栈顶符号
s1.push(sym2);
else
{
int pri = compare_priority(ope, (char)s1.top().a); //这里判断符号优先级 1大于 0相等 -1小于
if (pri >= 0)
{
s1.push(sym2);
}
else if (pri == -1) //若优先级小于栈顶符号,则将栈顶符号弹出压入S2,继续比较
{
s2.push(s1.top());
s1.pop();
goto label; //直接goto前面判断符号的开始位置
}
}
}
iter++; //别忘了更新迭代器位置
}
}
while (!s1.empty())
{
s2.push(s1.top());
s1.pop();
}
/*以下部分为存储前缀表达式*/
Poland prefix;
prefix.type = 'p';
prefix.lenth = s2.size();
prefix.content = new A[prefix.lenth]; //结构体中定义的是存储首地址,需要在这里开辟合适大小的数组空间,存储length个操作数或符号数据
int k = 0;
while (!s2.empty())
{
A res = s2.top();
A nres;
s2.pop();
if (res.type == 0)
{
string numm = to_string(res.a);
reverse(numm.begin(), numm.end()); //因为之前将中缀式颠倒时,数字也颠倒了。这里要改回来
nres.type = 0;
nres.a = atoi(numm.c_str());
}
else
{
nres.type = 1;
nres.a = res.a;
}
*(prefix.content + k) = nres;
k++;
}
return prefix;
}
3.求前缀表达式的值
①初始化一个栈S,从右往左扫描前缀式。
②遇到操作数时,则将其压入栈S。
③遇到运算符时,取出栈S的栈顶元素和次顶元素,运行运算。栈顶元素 运算符 次顶元素 = 结果。将结果压入栈S。
④重复②③直到到达前缀式最左边,此时栈S栈顶元素即为计算结果。
代码:
/*求前缀表达式的值*/
int cal_prefix(Poland prefix)
{
stack s;
int i = prefix.lenth - 1;
while (i >= 0)
{
A temp = *(prefix.content + i);
if (temp.type == 0)
{
s.push(temp);
}
else
{
A num1 = s.top();
s.pop();
A num2 = s.top();
s.pop();
A res;
res.type = 0;
if (temp.a == (int)'+')
{
res.a = num1.a + num2.a;
}
else if (temp.a == (int)'-')
{
res.a = num1.a - num2.a;
}
else if (temp.a == (int)'*')
{
res.a = num1.a * num2.a;
}
else if (temp.a == (int)'/')
{
res.a = num1.a / num2.a;
}
else if (temp.a == (int)'%')
{
res.a = num1.a % num2.a;
}
s.push(res);
}
i--;
}
return s.top().a;
}
4.中缀表达式转后缀表达式
与2类似,最主要的区别是,这里采用正序扫描。且左右括号的情况反过来了,且优先级比较处有微小区别,且最后结果要倒过来。
①初始化两个栈S1,S2,从右往左扫描中缀式。
②遇到操作数:将其压入S2栈。
③遇到括号时:
若是左括号‘(’,将其压入S1栈;
若是右括号‘)’,则依次弹出S1栈的元素,并将其压入S2栈,直至S1栈栈顶元素为左括号‘(’,弹出这个左括号。
④遇到运算符时:
若S1栈为空或者其栈顶元素为左括号‘(’,将其压入S1。
否则,比较运算符和S1栈顶运算符(一定是运算符)的优先级:
若其优先级>S1栈顶运算符,则将其压入S1;
若其优先级≤S1栈顶运算符,则将S1栈顶运算符弹出并压入S2,重新进行步骤④。
⑤重复②③④直到到达中缀式最右边。将S1剩余元素压入S2。最后依次取出S2元素进行倒序即为后缀表达式。
代码:
Poland infix_to_suffix(string infix)
{
stack s1, s2;
regex p("(\\d+)"); //用于查找数字的正则式
string s = infix;
string::const_iterator iter = s.begin();
string::const_iterator iter_end = s.end();
while (iter < iter_end)
{
smatch result;
if (iter >= iter_end) //防止迭代器位置超出字符串
break;
if (*iter >= '0'&&*iter <= '9') //遇操作数 这里不能直接用regex_search,必须要确定后面的字符串第一个字符是数字
{
regex_search(iter, iter_end, result, p);
string temp = result[0];
int num = atoi(temp.c_str()); //string转int c_str函数返回当前字符串的首字符地址
A sym1;
sym1.a = num;
sym1.type = 0;
s2.push(sym1);
iter = result[0].second; //别忘了更新迭代器位置,这里second表示查找到的数字在源串中后面部分串的首地址
}
else //遇符号
{
char ope = *iter;
A sym2;
sym2.a = (int)ope;
sym2.type = 1;
label:
if (ope == '(') //遇左括号,直接入栈
{
s1.push(sym2);
}
else if (ope == ')') //遇右括号,将栈内直到左括号之前的元素依次弹出压入S2
{
while (s1.top().a != (int)'(')
{
A t = s1.top();
s1.pop();
s2.push(t);
}
//这里让(也出栈
s1.pop();
}
else //其他运算符,如 %/* >= +-
{
if (s1.empty() || (s1.top().a == (int)'('&&s1.top().type == 1)) //若s1为空或其栈顶为(,符号入栈s1 或者符号优先级>栈顶符号
s1.push(sym2);
else
{
int pri = compare_priority(ope, (char)s1.top().a); //这里判断符号优先级 1大于 0相等 -1小于
if (pri > 0)
{
s1.push(sym2);
}
else if (pri == -1||pri==0) //若优先级小于等于栈顶符号,则将栈顶符号弹出压入S2,继续比较
{
s2.push(s1.top());
s1.pop();
goto label; //直接goto前面判断符号的开始位置
}
}
}
iter++; //别忘了更新迭代器位置
}
}
while (!s1.empty())
{
s2.push(s1.top());
s1.pop();
}
/*以下部分为存储后表达式*/
Poland suffix;
suffix.type = 's';
suffix.lenth = s2.size();
suffix.content = new A[suffix.lenth]; //结构体中定义的是存储首地址,需要在这里开辟合适大小的数组空间,存储length个操作数或符号数据
int k = suffix.lenth-1; //这里要倒过来
while (!s2.empty())
{
A res = s2.top();
A nres;
s2.pop();
if (res.type == 0)
{
string numm = to_string(res.a);
nres.type = 0;
nres.a = atoi(numm.c_str());
}
else
{
nres.type = 1;
nres.a = res.a;
}
*(suffix.content + k) = nres;
k--;
}
return suffix;
}
5.求后缀表达式的值
与3类似,同样这里要正序扫描,且次顶元素在运算符前。
①初始化一个栈S,从右往左扫描后缀式。
②遇到操作数时,则将其压入栈S。
③遇到运算符时,取出栈S的栈顶元素和次顶元素,运行运算。次顶元素 运算符 栈顶元素 = 结果。将结果压入栈S。
④重复②③直到到达前缀式最右边,此时栈S栈顶元素即为计算结果。
代码:
/*求后缀表达式的值*/
int cal_suffix(Poland suffix)
{
stack s;
int i = 0;
while (i < suffix.lenth)
{
A temp = *(suffix.content + i);
if (temp.type == 0)
{
s.push(temp);
}
else
{
A num2 = s.top();
s.pop();
A num1 = s.top();
s.pop();
A res;
res.type = 0;
if (temp.a == (int)'+')
{
res.a = num1.a + num2.a;
}
else if (temp.a == (int)'-')
{
res.a = num1.a - num2.a;
}
else if (temp.a == (int)'*')
{
res.a = num1.a * num2.a;
}
else if (temp.a == (int)'/')
{
res.a = num1.a / num2.a;
}
else if (temp.a == (int)'%')
{
res.a = num1.a % num2.a;
}
s.push(res);
}
i++;
}
return s.top().a;
}
6.测试
int main() // 9*8+(14-8/2)*3 =102 14-31%(19-8*2)+(56-33/(12-4)) =65
{
string infix;
cin >> infix;
Poland prefix = infix_to_prefix(infix);
Poland suffix = infix_to_suffix(infix);
cout << endl;
cout << "前缀表达式的长度为:" << prefix.lenth << endl;
for (auto i = 0; i < prefix.lenth; i++)
{
A temp = *(prefix.content + i);
string ts = "";
if (temp.type == 0)
ts += to_string(temp.a);
else
ts += (char)temp.a;
cout << ts << " ";
}
cout << endl;
cout <<"前缀表达式的计算值为:"<< cal_prefix(prefix) << endl;
cout << endl;
cout << "后缀表达式的长度为:" << suffix.lenth << endl;
for (auto i = 0; i < suffix.lenth; i++)
{
A temp = *(suffix.content + i);
string ts = "";
if (temp.type == 0)
ts += to_string(temp.a);
else
ts += (char)temp.a;
cout << ts << " ";
}
cout << endl;
cout << "后缀表达式的计算值为:" << cal_suffix(suffix) << endl;
return 0;
}
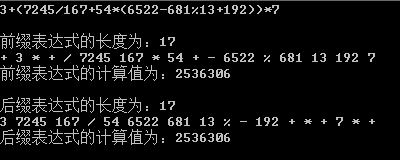
分别尝试了三组中缀表达式,结果如下:
9*8+(14-8/2)*3 =102

14-31%(19-8*2)+(56-33/(12-4)) =65
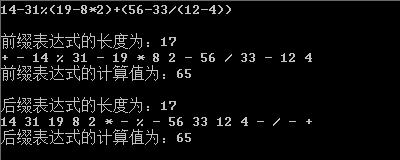
3+(7245/167+54*(6522-681%13+192))*7 =2536306