【VIO笔记（学习VINS的必备基础）】第五讲（1/2） 手写VIO后端

系列教程来自某学院，侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力，不然直接撸网上的各种VINS解析完全云里雾里-_-!

非线性最小二乘问题求解:solver

回忆上一讲的内容，最小二乘的系统可以表示为：

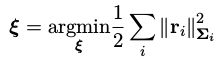
其中$\xi$是状态量，r表示残差，${\Sigma }_i$表示协方差。求解这个最小二乘实际上最后会落到迭代求下面这个正定方程：

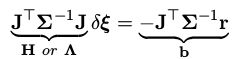
在上一讲里我们把它写成了连加形式，便于理解：

而要求解这个方程，直接取H的逆计算量大，上一讲提到使用舒尔补来求逆，具体来说，考虑纯视觉的BA问题，我们可以把$\mathbf{H}\Delta x=b$写成：

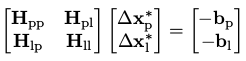
其中，下标p表示pose，下标l表示landmark，那么求$\Delta x$的问题可以看成分别求$\Delta x_p^{\ast }$和$\Delta x_l^{\ast }$，再拼接起来。例如我们先求$\Delta x_p^{\ast }$，利用舒尔补把H矩阵化为下三角：
$\left[\begin{array}{cc}{H}_{pp}^{\prime }& 0\\ X& X\end{array}\right]\left[\begin{array}{c}\Delta x_p^{\ast }\\ \Delta x_l^{\ast }\end{array}\right]=\left[\begin{array}{c}-b_p^{\prime }\\ -b_l^{\prime }\end{array}\right]$
对应的等式右边b也会发生变化，在这里等式左边H矩阵下面两项X的值不重要，使用第一行乘$\Delta x$可以得到变化后的b’，如下：

那么$\Delta x_p^{\ast }$可以表示为左边矩阵的逆乘等式右边，而这个矩阵的维度与之前的H相比降低了很多，方便求解，因为原H矩阵用图表示为下：

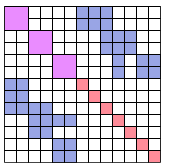
左上角是相机姿态，一个滑动窗口内只有十几个，而路标点往往会达到几百个，所以可以减少整个的计算量，得到了$\Delta x_p^{\ast }$后，通过原始的式子可以计算出$\Delta x_l^{\ast }$：

这样就计算出了整个$\Delta x$，那么接下来我们回顾一下求解器的整体流程图：

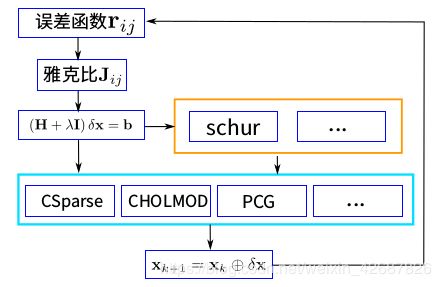
首先我们要确定误差函数r以及它的雅克比矩阵J，这个在第三讲里面已经讨论过了，之后我们利用最小二乘法求状态量的最佳估计，可以使用舒尔补等方法来进行计算，对于不是slam的问题会使用蓝色框里的一些方法来迭代求解，最后进行不断的迭代直到得到$x^{\ast }$。
最后我们要说一下求解过程中的一些问题，我们知道H矩阵通常不满秩，求解时无法直接求逆，所以我们使用LM法时，由于要添加一个阻尼因子，可以使得H矩阵满秩，然而由于相机都是相对的估计，所以会出现零空间变化的问题，通俗的说其优化后的轨迹的零点可能不是真实空间中的零点，为了解决这个问题，有以下几种方法：
1、添加先验。假设第一帧的x为零点，为了使其不会变化，我们给第一个pose的信息矩阵H加上一个单位阵I，即${\mathbf{H}}_{[11]}+=\mathbf{I}$，这样一来在展开的时候就有$\mathbf{I}\Delta x=0$，这样这一个$\Delta x$就只能为零了。
2、设定对应雅克比矩阵为 0,意味着残差等于 0. 求解方程为(0 + λI) $\Delta x$ = 0,只能$\Delta x$ = 0。
下面进入代码时间：

单目BA代码部分

这里的程序已经在github上开源：VINS-Course
首先我们手写一个后端来解决一个单目BA问题，代码的框架与g2o类似，可以分为顶点（vertex）、边（edge）、求解器（solver）三部分，顶点代表各个状态量，边代表残差、雅克比的计算、对应顶点的保存等等，求解器则负责计算正定方程等等。
整个代码的结构如下：

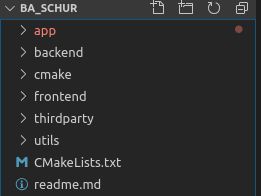
app放置应用问题的函数，例如这里是slam的BA问题，backend里涵盖后端的相应库函数，我们先来看BA问题：

/*
 * Frame : 保存每帧的姿态和观测
 */
struct Frame {
    Frame(Eigen::Matrix3d R, Eigen::Vector3d t) : Rwc(R), qwc(R), twc(t) {};
    Eigen::Matrix3d Rwc;
    Eigen::Quaterniond qwc;
    Eigen::Vector3d twc;

    unordered_map<int, Eigen::Vector3d> featurePerId; // 该帧观测到的特征以及特征id
};

/*
 * 产生世界坐标系下的虚拟数据: 相机姿态, 特征点, 以及每帧观测
 */
void GetSimDataInWordFrame(vector<Frame> &cameraPoses, vector<Eigen::Vector3d> &points) {
    int featureNums = 20;  // 特征数目，假设每帧都能观测到所有的特征
    int poseNums = 3;     // 相机数目

    double radius = 8;
    for (int n = 0; n < poseNums; ++n) {
        double theta = n * 2 * M_PI / (poseNums * 4); // 1/4 圆弧
        // 绕 z轴 旋转
        Eigen::Matrix3d R;
        R = Eigen::AngleAxisd(theta, Eigen::Vector3d::UnitZ());
        Eigen::Vector3d t = Eigen::Vector3d(radius * cos(theta) - radius, radius * sin(theta), 1 * sin(2 * theta));
        cameraPoses.push_back(Frame(R, t));
    }

    // 随机数生成三维特征点
    std::default_random_engine generator;
    std::normal_distribution<double> noise_pdf(0., 1. / 1000.);  // 2pixel / focal
    for (int j = 0; j < featureNums; ++j) {
        std::uniform_real_distribution<double> xy_rand(-4, 4.0);
        std::uniform_real_distribution<double> z_rand(4., 8.);

        Eigen::Vector3d Pw(xy_rand(generator), xy_rand(generator), z_rand(generator));
        points.push_back(Pw);

        // 在每一帧上的观测量
        for (int i = 0; i < poseNums; ++i) {
            Eigen::Vector3d Pc = cameraPoses[i].Rwc.transpose() * (Pw - cameraPoses[i].twc);
            Pc = Pc / Pc.z();  // 归一化图像平面
            Pc[0] += noise_pdf(generator);
            Pc[1] += noise_pdf(generator);
            cameraPoses[i].featurePerId.insert(make_pair(j, Pc));
        }
    }
}

首先定义了fram结构体和生成数据的函数GetSimDataInWordFrame，这部分比较简单，噪声用正态分布去模拟的。主函数：

int main() {
    // 准备数据
    vector<Frame> cameras;
    vector<Eigen::Vector3d> points;
    GetSimDataInWordFrame(cameras, points);
    Eigen::Quaterniond qic(1, 0, 0, 0);
    Eigen::Vector3d tic(0, 0, 0);

    // 构建 problem
    Problem problem(Problem::ProblemType::SLAM_PROBLEM);

    // 所有 Pose
    vector<shared_ptr<VertexPose> > vertexCams_vec;
    for (size_t i = 0; i < cameras.size(); ++i) {
        shared_ptr<VertexPose> vertexCam(new VertexPose());
        Eigen::VectorXd pose(7);
        pose << cameras[i].twc, cameras[i].qwc.x(), cameras[i].qwc.y(), cameras[i].qwc.z(), cameras[i].qwc.w();
        vertexCam->SetParameters(pose);

//        if(i < 2)
//            vertexCam->SetFixed();

        problem.AddVertex(vertexCam);
        vertexCams_vec.push_back(vertexCam);
    }

    // 所有 Point 及 edge
    std::default_random_engine generator;
    std::normal_distribution<double> noise_pdf(0, 1.);
    double noise = 0;
    vector<double> noise_invd;
    vector<shared_ptr<VertexInverseDepth> > allPoints;
    for (size_t i = 0; i < points.size(); ++i) {
        //假设所有特征点的起始帧为第0帧， 逆深度容易得到
        Eigen::Vector3d Pw = points[i];
        Eigen::Vector3d Pc = cameras[0].Rwc.transpose() * (Pw - cameras[0].twc);
        noise = noise_pdf(generator);
        double inverse_depth = 1. / (Pc.z() + noise);
//        double inverse_depth = 1. / Pc.z();
        noise_invd.push_back(inverse_depth);

        // 初始化特征 vertex
        shared_ptr<VertexInverseDepth> verterxPoint(new VertexInverseDepth());
        VecX inv_d(1);
        inv_d << inverse_depth;
        verterxPoint->SetParameters(inv_d);
        problem.AddVertex(verterxPoint);
        allPoints.push_back(verterxPoint);

        // 每个特征对应的投影误差, 第 0 帧为起始帧
        for (size_t j = 1; j < cameras.size(); ++j) {
            Eigen::Vector3d pt_i = cameras[0].featurePerId.find(i)->second;
            Eigen::Vector3d pt_j = cameras[j].featurePerId.find(i)->second;
            shared_ptr<EdgeReprojection> edge(new EdgeReprojection(pt_i, pt_j));
            edge->SetTranslationImuFromCamera(qic, tic);

            std::vector<std::shared_ptr<Vertex> > edge_vertex;
            edge_vertex.push_back(verterxPoint);
            edge_vertex.push_back(vertexCams_vec[0]);
            edge_vertex.push_back(vertexCams_vec[j]);
            edge->SetVertex(edge_vertex);

            problem.AddEdge(edge);
        }
    }

    problem.Solve(5);

    std::cout << "\nCompare MonoBA results after opt..." << std::endl;
    for (size_t k = 0; k < allPoints.size(); k+=1) {
        std::cout << "after opt, point " << k << " : gt " << 1. / points[k].z() << " ,noise "
                  << noise_invd[k] << " ,opt " << allPoints[k]->Parameters() << std::endl;
    }
    std::cout<<"------------ pose translation ----------------"<<std::endl;
    for (int i = 0; i < vertexCams_vec.size(); ++i) {
        std::cout<<"translation after opt: "<< i <<" :"<< vertexCams_vec[i]->Parameters().head(3).transpose() << " || gt: "<<cameras[i].twc.transpose()<<std::endl;
    }
    /// 优化完成后，第一帧相机的 pose 平移（x,y,z）不再是原点 0,0,0. 说明向零空间发生了漂移。
    /// 解决办法： fix 第一帧和第二帧，固定 7 自由度。 或者加上非常大的先验值。

    problem.TestMarginalize();

    return 0;
}

可以看到这里的顶点有vertexpose和vertexcam两种，

后端的部分：

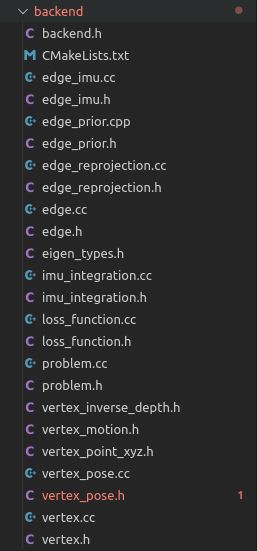
之前说到的顶点、边、求解器这里都有对应的文件，所有顶点对应的父类为vertex，它有一个VecX来表示它的值，然后还要指定其维度。以姿态的顶点VertexPose为例：

class VertexPose : public Vertex {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    VertexPose() : Vertex(7, 6) {}

    /// 加法，可重定义
    /// 默认是向量加
    virtual void Plus(const VecX &delta) override;

    std::string TypeInfo() const {
        return "VertexPose";
    }
};

构造函数的两项参数为其变量的维数和实际自由度，比如姿态有6个自由度但是由于使用了四元数表示所以一共7维，这里就是7和6。同时对加法进行了override：

void VertexPose::Plus(const VecX &delta) {
    VecX &parameters = Parameters();
    parameters.head<3>() += delta.head<3>();
    Qd q(parameters[6], parameters[3], parameters[4], parameters[5]);
    q = q * Sophus::SO3d::exp(Vec3(delta[3], delta[4], delta[5])).unit_quaternion();  // right multiplication with so3
    q.normalized();
    parameters[3] = q.x();
    parameters[4] = q.y();
    parameters[5] = q.z();
    parameters[6] = q.w();
}

平移部分直接相加，旋转部分需要先将四元数的虚部转换为SO3下的更新量，再右乘原来的四元数，得到更新后的四元数，之后对四元数进行了归一化。
对于边来说，边负责计算残差，残差是（预测-观测），维度在构造函数中定义代价函数是 （残差×信息×残差），是一个数值，由后端求和后最小化。edge类的构造函数如下：

    /**
     * 构造函数，会自动化配雅可比的空间
     * @param residual_dimension 残差维度
     * @param num_verticies 顶点数量
     * @param verticies_types 顶点类型名称，可以不给，不给的话check中不会检查
     */
    explicit Edge(int residual_dimension, int num_verticies,
                  const std::vector<std::string> &verticies_types = std::vector<std::string>());

以在BA里使用的重投影误差的边EdgeReprojection为例说明：

/**
 * 此边是视觉重投影误差，此边为三元边，与之相连的顶点有：
 * 路标点的逆深度InveseDepth、第一次观测到该路标点的source Camera的位姿T_World_From_Body1，
 * 和观测到该路标点的mearsurement Camera位姿T_World_From_Body2。
 * 注意：verticies_顶点顺序必须为InveseDepth、T_World_From_Body1、T_World_From_Body2。
 */
class EdgeReprojection : public Edge {
public:
    EIGEN_MAKE_ALIGNED_OPERATOR_NEW;

    EdgeReprojection(const Vec3 &pts_i, const Vec3 &pts_j)
        : Edge(2, 3, std::vector<std::string>{"VertexInverseDepth", "VertexPose", "VertexPose"}) {
        pts_i_ = pts_i;
        pts_j_ = pts_j;
    }

    /// 返回边的类型信息
    virtual std::string TypeInfo() const override { return "EdgeReprojection"; }

    /// 计算残差
    virtual void ComputeResidual() override;

    /// 计算雅可比
    virtual void ComputeJacobians() override;

    void SetTranslationImuFromCamera(Eigen::Quaterniond &qic_, Vec3 &tic_);

private:
    //Translation imu from camera
    Qd qic;
    Vec3 tic;

    //measurements
    Vec3 pts_i_, pts_j_;
};

这里传入的pts_i和pts_j，分别是当前观测和上一帧观测的重投影的像素坐标，并且在归一化平面上，即z=1。前面说到edge要负责计算出顶点残差和其对应的雅克比，这部分的函数如下，在cpp文件中：

/*    std::vector> verticies_; // 该边对应的顶点
    VecX residual_;                 // 残差
    std::vector jacobians_;  // 雅可比，每个雅可比维度是 residual x vertex[i]
    MatXX information_;             // 信息矩阵
    VecX observation_;              // 观测信息
    */

void EdgeReprojection::ComputeResidual() {
    double inv_dep_i = verticies_[0]->Parameters()[0];

    VecX param_i = verticies_[1]->Parameters();
    Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]);
    Vec3 Pi = param_i.head<3>();

    VecX param_j = verticies_[2]->Parameters();
    Qd Qj(param_j[6], param_j[3], param_j[4], param_j[5]);
    Vec3 Pj = param_j.head<3>();

    Vec3 pts_camera_i = pts_i_ / inv_dep_i;
    Vec3 pts_imu_i = qic * pts_camera_i + tic;
    Vec3 pts_w = Qi * pts_imu_i + Pi;
    Vec3 pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Vec3 pts_camera_j = qic.inverse() * (pts_imu_j - tic);

    double dep_j = pts_camera_j.z();
    residual_ = (pts_camera_j / dep_j).head<2>() - pts_j_.head<2>();   /// J^t * J * delta_x = - J^t * r
}

首先计算残差，这里的残差是按照第三讲中的视觉重投影误差计算的，首先取得i帧下的逆深度，然后获得两帧相机的姿态，之后通过坐标系的转换将i帧下的像素点坐标pts_i_转换到j帧的坐标系下，最后将转换过来的像素坐标(pts_camera_j / dep_j)和j帧下的测量值取差得到残差。

void EdgeReprojection::ComputeJacobians() {
    double inv_dep_i = verticies_[0]->Parameters()[0];

    VecX param_i = verticies_[1]->Parameters();
    Qd Qi(param_i[6], param_i[3], param_i[4], param_i[5]);
    Vec3 Pi = param_i.head<3>();

    VecX param_j = verticies_[2]->Parameters();
    Qd Qj(param_j[6], param_j[3], param_j[4], param_j[5]);
    Vec3 Pj = param_j.head<3>();

    Vec3 pts_camera_i = pts_i_ / inv_dep_i;
    Vec3 pts_imu_i = qic * pts_camera_i + tic;
    Vec3 pts_w = Qi * pts_imu_i + Pi;
    Vec3 pts_imu_j = Qj.inverse() * (pts_w - Pj);
    Vec3 pts_camera_j = qic.inverse() * (pts_imu_j - tic);

    double dep_j = pts_camera_j.z();

    Mat33 Ri = Qi.toRotationMatrix();
    Mat33 Rj = Qj.toRotationMatrix();
    Mat33 ric = qic.toRotationMatrix();
    Mat23 reduce(2, 3);
    reduce << 1. / dep_j, 0, -pts_camera_j(0) / (dep_j * dep_j),
        0, 1. / dep_j, -pts_camera_j(1) / (dep_j * dep_j);
//    reduce = information_ * reduce;

    Eigen::Matrix<double, 2, 6> jacobian_pose_i;
    Eigen::Matrix<double, 3, 6> jaco_i;
    jaco_i.leftCols<3>() = ric.transpose() * Rj.transpose();
    jaco_i.rightCols<3>() = ric.transpose() * Rj.transpose() * Ri * -Sophus::SO3d::hat(pts_imu_i);
    jacobian_pose_i.leftCols<6>() = reduce * jaco_i;

    Eigen::Matrix<double, 2, 6> jacobian_pose_j;
    Eigen::Matrix<double, 3, 6> jaco_j;
    jaco_j.leftCols<3>() = ric.transpose() * -Rj.transpose();
    jaco_j.rightCols<3>() = ric.transpose() * Sophus::SO3d::hat(pts_imu_j);
    jacobian_pose_j.leftCols<6>() = reduce * jaco_j;

    Eigen::Vector2d jacobian_feature;
    jacobian_feature = reduce * ric.transpose() * Rj.transpose() * Ri * ric * pts_i_ * -1.0 / (inv_dep_i * inv_dep_i);

    jacobians_[0] = jacobian_feature;
    jacobians_[1] = jacobian_pose_i;
    jacobians_[2] = jacobian_pose_j;
}

雅克比的计算同样和第三讲中一样，前面计算逆深度、各个变换矩阵的过程和计算残差的相同，reduce矩阵对应链式计算中的$\frac{\partial r_c}{\partial f_{c_j}}$，之后分别计算了$f_{c_j}$对各个状态量的导数，以对i时刻pose的导数为例：先计算出对位移的导数

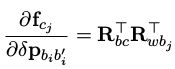
对应jaco_j.leftCols<3>() = ric.transpose() * Rj.transpose();之后是对角度的偏导，hat表示对fbi即程序中的pts_imu_j求反对称矩阵，最后再乘上reduce就得到了残差rc对i时刻pose的偏导。
其他两个状态量j时刻的pose和逆深度的求导，同样根据第三讲推导的公式来就可以了。最后得到整个视觉重投影误差的雅克比矩阵。
到这里edge的结构差不多就清楚了，接下来进入problem类：该类函数较多，我们从主函数用到的顺序来看，Problem problem(Problem::ProblemType::SLAM_PROBLEM);首先构造problem对象，有SLAM和普通两种类型，这里我们用SLAM类，之后向problem中加入了顶点和边：

bool Problem::AddVertex(std::shared_ptr<Vertex> vertex) {
    if (verticies_.find(vertex->Id()) != verticies_.end()) {
        LOG(WARNING) << "Vertex " << vertex->Id() << " has been added before";
        return false;
    } else {
        verticies_.insert(pair<unsigned long, shared_ptr<Vertex>>(vertex->Id(), vertex));
    }

    if (problemType_ == ProblemType::SLAM_PROBLEM) {
        if (IsPoseVertex(vertex)) {
            ResizePoseHessiansWhenAddingPose(vertex);
        }
    }
    return true;
}

以添加顶点为例，函数会给顶点添加一个序号，同时根据顶点是否为pose来生成H矩阵，例如第一个pose在左上角00位置，第二个应该左上角就为66。添加完顶点和边后，主函数直接调用solve方法就结束了，我们来看一下solve函数：

bool Problem::Solve(int iterations) {
    if (edges_.size() == 0 || verticies_.size() == 0) {
        std::cerr << "\nCannot solve problem without edges or verticies" << std::endl;
        return false;
    }
    TicToc t_solve;
    // 统计优化变量的维数，为构建 H 矩阵做准备
    SetOrdering();
    // 遍历edge, 构建 H 矩阵
    MakeHessian();
    // LM 初始化
    ComputeLambdaInitLM();
    // LM 算法迭代求解
    bool stop = false;
    int iter = 0;
    while (!stop && (iter < iterations)) {
        std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_ << std::endl;
        bool oneStepSuccess = false;
        int false_cnt = 0;
        while (!oneStepSuccess)  // 不断尝试 Lambda, 直到成功迭代一步
        {
            // setLambda
//            AddLambdatoHessianLM();
            // 第四步，解线性方程
            SolveLinearSystem();
            //
//            RemoveLambdaHessianLM();

            // 优化退出条件1： delta_x_ 很小则退出
            if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
                stop = true;
                break;
            }

            // 更新状态量
            UpdateStates();
            // 判断当前步是否可行以及 LM 的 lambda 怎么更新
            oneStepSuccess = IsGoodStepInLM();
            // 后续处理，
            if (oneStepSuccess) {
                // 在新线性化点 构建 hessian
                MakeHessian();
                // TODO:: 这个判断条件可以丢掉，条件 b_max <= 1e-12 很难达到，这里的阈值条件不应该用绝对值，而是相对值
//                double b_max = 0.0;
//                for (int i = 0; i < b_.size(); ++i) {
//                    b_max = max(fabs(b_(i)), b_max);
//                }
//                // 优化退出条件2： 如果残差 b_max 已经很小了，那就退出
//                stop = (b_max <= 1e-12);
                false_cnt = 0;
            } else {
                false_cnt ++;
                RollbackStates();   // 误差没下降，回滚
            }
        }
        iter++;

        // 优化退出条件3： currentChi_ 跟第一次的chi2相比，下降了 1e6 倍则退出
        if (sqrt(currentChi_) <= stopThresholdLM_)
            stop = true;
    }
    std::cout << "problem solve cost: " << t_solve.toc() << " ms" << std::endl;
    std::cout << "   makeHessian cost: " << t_hessian_cost_ << " ms" << std::endl;
    return true;
}

这里用到的是第四讲求解最小二乘的内容，首先通过SetOrdering()函数统计待优化状态量的维度，之后通过MakeHessian()构建H矩阵，也就是我们第四讲说的信息矩阵$\Lambda$。这里需要我们补充一些代码：

for (size_t i = 0; i < verticies.size(); ++i) {
            auto v_i = verticies[i];
            if (v_i->IsFixed()) continue;    // Hessian 里不需要添加它的信息，也就是它的雅克比为 0

            auto jacobian_i = jacobians[i];
            ulong index_i = v_i->OrderingId();
            ulong dim_i = v_i->LocalDimension();

            MatXX JtW = jacobian_i.transpose() * edge.second->Information();
            for (size_t j = i; j < verticies.size(); ++j) {
                auto v_j = verticies[j];

                if (v_j->IsFixed()) continue;

                auto jacobian_j = jacobians[j];
                ulong index_j = v_j->OrderingId();
                ulong dim_j = v_j->LocalDimension();

                assert(v_j->OrderingId() != -1);
                MatXX hessian = JtW * jacobian_j;
                // 所有的信息矩阵叠加起来
                H.block(index_i,index_j, dim_i, dim_j).noalias() += hessian;
                if (j != i) {
                    // 对称的下三角
                    H.block(index_j,index_i, dim_j, dim_i).noalias() += hessian.transpose();
                }
            }
            b.segment(index_i, dim_i).noalias() -= JtW * edge.second->Residual();
        }

这是在遍历所有的edge的代码内部构建H矩阵的过程，对于每一条边都要进行这样两个for循环，分别是遍历方阵H的行和列，第一个i的for循环是行数，当遍历到行列相等，也就是对角的时候，只用放入一次hessian，而其他情况下都要放入关于对角对称的两个hessian，这是由于这两个位置的hessian是转置的关系。而b则在行遍历的时候一行行填入就可以了。
这一讲由于涉及很多程序讲解，为避免篇幅过长，分开为两个博客。