【VIO笔记（学习VINS的必备基础）】第五讲（2/2） 手写VIO后端

系列教程来自某学院，侵权删除。
学习完这一系列课程再去看VINS才能做到不吃力，不然直接撸网上的各种VINS解析完全云里雾里-_-!

上接第五讲1/2。

单目BA程序

上一讲讲到了H矩阵的构建，之后就要进行LM算法的初始化，ComputeLambdaInitLM()函数用于计算阻尼因子的初始值，在第三讲中说到过，阻尼因子的初始值选取方式为：

其中$\tau$是一个系数，按工程经验取值，程序里这个值取了10^-5double tau = 1e-5;，最后阻尼因子的计算为currentLambda_ = tau * maxDiagonal;maxdiagonal是H矩阵对角线上最大的块。
初始化完成之后就进入LM迭代求解的部分，迭代次数由solve函数的入口参数确定，这是最后的运行结果截图，可以看到迭代了5次，

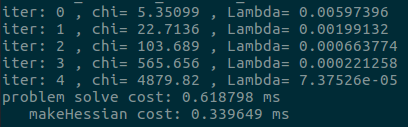
下面我们来看一次迭代中，LM算法是怎么实现的，方便阅读再把程序放上来一次：

    while (!stop && (iter < iterations)) {
        std::cout << "iter: " << iter << " , chi= " << currentChi_ << " , Lambda= " << currentLambda_ << std::endl;
        bool oneStepSuccess = false;
        int false_cnt = 0;
        while (!oneStepSuccess)  // 不断尝试 Lambda, 直到成功迭代一步
        {
        	// 解Hx=b
            SolveLinearSystem();
            // 优化退出条件1： delta_x_ 很小则退出
            if (delta_x_.squaredNorm() <= 1e-6 || false_cnt > 10) {
                stop = true;
                break;
            }
            // 更新状态量
            UpdateStates();
            // 判断当前步是否可行以及 LM 的 lambda 怎么更新
            oneStepSuccess = IsGoodStepInLM();
            // 后续处理，
            if (oneStepSuccess) {
                // 在新线性化点 构建 hessian
                MakeHessian();
                false_cnt = 0;
            } else {
                false_cnt ++;
                RollbackStates();   // 误差没下降，回滚
            }
        }
        iter++;
        // 优化退出条件2： currentChi_ 跟第一次的chi2相比，下降了 1e6 倍则退出
        if (sqrt(currentChi_) <= stopThresholdLM_)
            stop = true;
    }

首先使用SolveLinearSystem();来求解$\Delta x$，如果求解后$\Delta x$的值够小则认为迭代成功，令stop = true;退出while循环，否则更新状态量并判断当前步是否可行，可行的话就在当前的状态量下求新的H和b，否则当发现误差没有下降的时候就进行回滚。同时如果当残差下降得够多也可以退出迭代。
求解完problem整个问题BA就结束了，最后主函数里还有一个边缘化的测试函数，对应的是第四讲里的例子，假设有

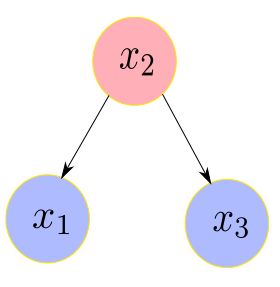
对应的信息矩阵为

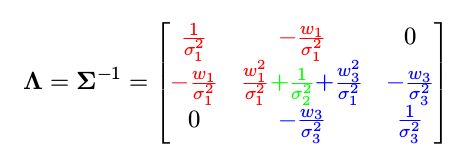
现在要从这个例子中marg掉x2，那么要求之后的信息矩阵。程序如下：

void Problem::TestMarginalize() {

    // Add marg test
    int idx = 1;            // marg 中间那个变量
    int dim = 1;            // marg 变量的维度
    int reserve_size = 3;   // 总共变量的维度
    double delta1 = 0.1 * 0.1;
    double delta2 = 0.2 * 0.2;
    double delta3 = 0.3 * 0.3;

    int cols = 3;
    MatXX H_marg(MatXX::Zero(cols, cols));
    H_marg << 1./delta1, -1./delta1, 0,
            -1./delta1, 1./delta1 + 1./delta2 + 1./delta3, -1./delta3,
            0.,  -1./delta3, 1/delta3;
    std::cout << "---------- TEST Marg: before marg------------"<< std::endl;
    std::cout << H_marg << std::endl;

    // TODO:: home work. 将变量移动到右下角
    /// 准备工作： move the marg pose to the Hmm bottown right
    // 将 row i 移动矩阵最下面
    Eigen::MatrixXd temp_rows = H_marg.block(idx, 0, dim, reserve_size);
    Eigen::MatrixXd temp_botRows = H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size);
    H_marg.block(idx, 0, dim, reserve_size) = temp_botRows;
    H_marg.block(idx + dim, 0, reserve_size - idx - dim, reserve_size) = temp_rows;

    // 将 col i 移动矩阵最右边
    Eigen::MatrixXd temp_cols = H_marg.block(0, idx, reserve_size, dim);
    Eigen::MatrixXd temp_rightCols = H_marg.block(0, idx + dim, reserve_size, reserve_size - idx - dim);
    H_marg.block(0, idx, reserve_size, reserve_size - idx - dim) = temp_rightCols;
    H_marg.block(0, reserve_size - dim, reserve_size, dim) = temp_cols;

    std::cout << "---------- TEST Marg: 将变量移动到右下角------------"<< std::endl;
    std::cout<< H_marg <<std::endl;

    /// 开始 marg ： schur
    double eps = 1e-8;
    int m2 = dim;
    int n2 = reserve_size - dim;   // 剩余变量的维度
    Eigen::MatrixXd Amm = 0.5 * (H_marg.block(n2, n2, m2, m2) + H_marg.block(n2, n2, m2, m2).transpose());

    Eigen::SelfAdjointEigenSolver<Eigen::MatrixXd> saes(Amm);
    Eigen::MatrixXd Amm_inv = saes.eigenvectors() * Eigen::VectorXd(
            (saes.eigenvalues().array() > eps).select(saes.eigenvalues().array().inverse(), 0)).asDiagonal() *
                              saes.eigenvectors().transpose();

    // TODO:: home work. 完成舒尔补操作
    Eigen::MatrixXd Arm = H_marg.block(0,n2,n2,m2);
    Eigen::MatrixXd Amr = H_marg.block(n2,0,m2,n2);
    Eigen::MatrixXd Arr = H_marg.block(0,0,n2,n2);

    Eigen::MatrixXd tempB = Arm * Amm_inv;
    Eigen::MatrixXd H_prior = Arr - tempB * Amr;

    std::cout << "---------- TEST Marg: after marg------------"<< std::endl;
    std::cout << H_prior << std::endl;
}

操作的流程是先将待marg的状态量移动到信息矩阵的右下角，之后将矩阵化为四个矩阵块，根据之前的流程：

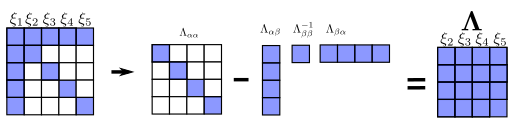
即可得到新的信息矩阵，最后我的运行结果如下：

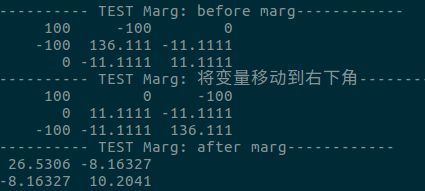
VINS中的滑动窗口算法

滑动窗口中的问题

1、先验残差
之前第四讲中已经说到先验残差由于已经被marg掉了所以固定不变，那么能不能更新先验残差呢?其实是可以的，虽然先验信息矩阵固定不变,但随着迭代的推进,变量被不断优化,先验残差需要跟随变化。否则,求解系统可能奔溃。
方法:先验残差的变化可以使用一阶泰勒近似。

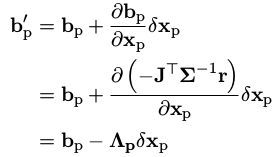
这样就？？？？
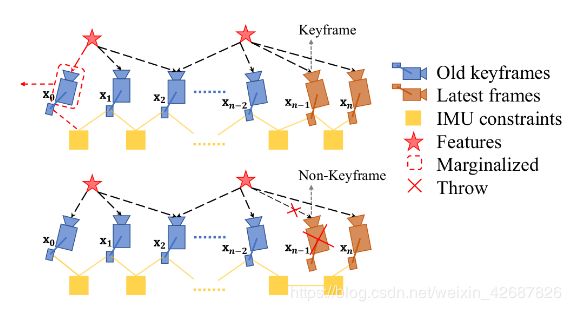
2、marg选取问题
在vins中需要对滑动窗口中下一个marg掉的帧进行选择：
• 当滑动窗口中第二新的图像帧为关键帧,则 marg 最老的帧,以及上面的路标点。
• 当滑动窗口中第二新的图像帧不是关键帧,则丢弃这一帧上的视觉测量信息，IMU 预积分传给下一帧。