机器学习——逻辑回归(分类)
前言:真的是改了很多次!细节真的很多!
机器学习专栏:机器学习专栏
文章目录
- 逻辑回归(分类)
- 1、基本原理
- 4、梯度下降法
- 4、sklearn实现逻辑回归
- 5、多分类问题
- 5.1多分类原理
- 5.2sklearn实现多分类
逻辑回归(分类)
1、基本原理
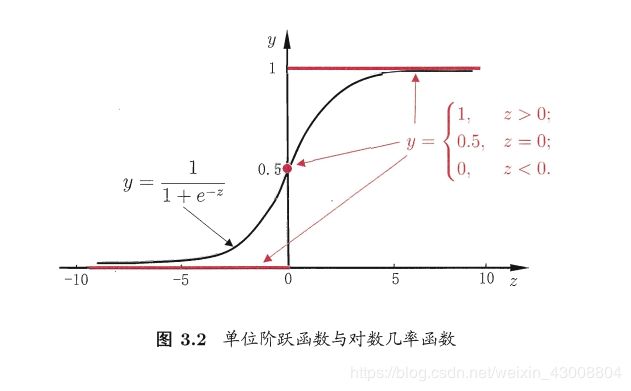
逻辑回归用于分类,是对样本属于某一类的概率进行预测,对数几率函数:
g ( z ) = 1 1 + e − z g(z)=\frac{1}{1+e^{-z}} g(z)=1+e−z1

给定数据集 D = ( x ( 1 ) , y ( 1 ) ) ; ( x ( 2 ) , y ( 2 ) ) ; . . . ; ( x ( m ) , y ( i ) ) D={(x^{(1)},y^{(1)});(x^{(2)},y^{(2)});...;(x^{(m)},y^{(i)} )} D=(x(1),y(1));(x(2),y(2));...;(x(m),y(i)),其中 x ( i ) x^{(i)} x(i)表示第 i i i个样本点 x ( i ) ∈ R n x^{(i)}\in{R^n} x(i)∈Rn(表示有n个属性值)。
考虑到 y = θ 0 + θ 1 x 1 ( i ) + . . . + θ n x n ( i ) y=\theta_0+\theta_1 x^{(i)}_1+...+\theta_nx^{(i)}_n y=θ0+θ1x1(i)+...+θnxn(i)取值是连续的,因此它不能拟合离散变量。可以考虑用它来拟合条件概率 ,因为概率的取值也是连续的。但是其取值为 R ,不符合概率取值为 0 到 1,因此考虑采用广义线性模型。
对于一个简单的二分类问题,我们用logistics函数来代替理想的阶跃函数来作为连接函数:
h θ ( x ( i ) ) = 1 1 + e − θ T x ( i ) h_\theta(x^{(i)})=\frac{1}{1+e^{-\theta^Tx^{(i)}}} hθ(x(i))=1+e−θTx(i)1
令 z = θ T x ( i ) z=\theta^Tx^{(i)} z=θTx(i)
于是有:
l n h θ ( x ( i ) ) 1 − h θ ( x ( i ) ) = θ T x ( i ) ln\frac{h_\theta(x^{(i)})}{1-h_\theta(x^{(i)})}=\theta^T x^{(i)} ln1−hθ(x(i))hθ(x(i))=θTx(i)
事件发生与不发生的概率比值称为几率(odds), h θ ( x ( i ) ) h_\theta(x^{(i)}) hθ(x(i))表示发生的概率,即:
{ P ( y = 1 ∣ x ( i ) , θ ) = h θ ( x ( i ) ) P ( y = 0 ∣ x ( i ) , θ ) = 1 − h θ ( x ( i ) ) \left\{\begin{matrix} P(y=1|x^{(i)},\theta)=h_\theta(x^{(i)})\\ P(y=0|x^{(i)},\theta)=1-h_\theta(x^{(i)}) \end{matrix}\right. {P(y=1∣x(i),θ)=hθ(x(i))P(y=0∣x(i),θ)=1−hθ(x(i))
综合两式可得:
P ( y ∣ x ( i ) ; θ ) = ( h θ ( x ( i ) ) ) y ( 1 − h θ ( x ( i ) ) ) 1 − y P(y|x^{(i)};\theta)=(h_\theta(x^{(i)}))^y(1-h_\theta(x^{(i)}))^{1-y} P(y∣x(i);θ)=(hθ(x(i)))y(1−hθ(x(i)))1−y
因此逻辑回归的思路是,先拟合决策边界(不局限于线性,还可以是多项式,这个过程可以理解为感知机),再建立这个边界与分类的概率联系(通过对数几率函数),从而得到了二分类情况下的概率。
关于对数似然估计的概念我这里就不作过多介绍了,可参考浙江大学的《概率论与数理统计》,我们由“最大似然估计法”去得出代价函数,我们要求每个样本属于其真实标记的概率越大越好,所以:
m a x L ( θ ) = ∏ i = 1 m P ( y ( i ) ∣ x ( i ) , θ ) max\quad L(\theta)=\prod_{i=1}^{m}P(y^{(i)}|x^{(i)},\theta) maxL(θ)=i=1∏mP(y(i)∣x(i),θ)
取“对数似然”得:
m a x l o g L ( θ ) = ∑ i = 1 m l o g P ( y ( i ) ∣ x ( i ) , θ ) max\quad logL(\theta)=\sum_{i=1}^{m}logP(y^{(i)}|x^{(i)},\theta) maxlogL(θ)=i=1∑mlogP(y(i)∣x(i),θ)
由上,我们将代价函数定为:
J ( θ ) = 1 m ∑ i = 1 m C ( h θ ( x ( i ) ) , y ( i ) ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) ] J(\theta)=\frac{1}{m}\sum_{i=1}^{m}C(h_\theta(x^{(i)}),y^{(i)})=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)}))] J(θ)=m1i=1∑mC(hθ(x(i)),y(i))=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))]
一次性计算出所有样本的预测值(是个概率值):
h = g ( X θ ) h=g(X\theta) h=g(Xθ)
其中, X = [ x 0 1 x 1 1 . . . x n 1 x 0 2 x 1 1 . . . x n 1 : : . . . : x 0 m x 1 m . . . x n m ] X=\begin{bmatrix} x_0^1 & x_1^1 &... &x_n^1 \\ x_0^2 & x_1^1 &... &x_n^1 \\ : & : &... &:\\ x_0^m & x_1^m &... &x_n^m \end{bmatrix} X=⎣⎢⎢⎡x01x02:x0mx11x11:x1m............xn1xn1:xnm⎦⎥⎥⎤表示训练集, θ = [ θ 0 θ 1 : θ n ] \theta=\begin{bmatrix} \theta_0\\ \theta_1\\ :\\ \theta_n\end{bmatrix} θ=⎣⎢⎢⎡θ0θ1:θn⎦⎥⎥⎤
将代价函数写成矩阵形式:
J ( θ ) = − 1 m ( Y T l o g ( h ) − ( 1 − Y ) T l o g ( 1 − h ) ) J(\theta)=-\frac{1}{m}(Y^Tlog(h)-(1-Y)^Tlog(1-h)) J(θ)=−m1(YTlog(h)−(1−Y)Tlog(1−h))
其中, Y = [ y ( 1 ) y ( 2 ) : y ( m ) ] Y=\begin{bmatrix} y^{(1)}\\ y^{(2)}\\ :\\ y^{(m)}\end{bmatrix} Y=⎣⎢⎢⎡y(1)y(2):y(m)⎦⎥⎥⎤表示由所有训练样本输出构成的向量, h = [ h ( 1 ) h ( 2 ) : h ( m ) ] h=\begin{bmatrix} h(1)\\ h(2)\\ :\\ h(m) \end{bmatrix} h=⎣⎢⎢⎡h(1)h(2):h(m)⎦⎥⎥⎤表示计算得出所有样本的预测值(是个概率值)
4、梯度下降法
梯度下降公式:
θ j : = θ j − α m ∂ ∂ θ j J ( θ ) θ j : = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\frac{\alpha}{m}\frac{\partial}{\partial\theta_j}J(\theta) \\ \theta_j:=\theta_j-\frac{\alpha}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−mα∂θj∂J(θ)θj:=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)
【logistics回归梯度下降公式的简单推导】
θ j : = θ j − α m ∂ ∂ θ j J ( θ ) J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( h θ ( x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − h θ ( x ( i ) ) ) J ( θ ) = − 1 m ∑ i = 1 m [ y ( i ) l o g ( g ( θ T x ( i ) ) ) + ( 1 − y ( i ) ) l o g ( 1 − g ( θ T x ( i ) ) ) ∂ J ( θ ) ∂ θ j = − 1 m ∑ i = 1 m [ y ( i ) g ( θ T x ( i ) ) − ( 1 − y ( i ) ) 1 1 − g ( θ T x ( i ) ) ] ∂ g ( θ T x ( i ) ) ∂ θ j 先 求 : ∂ g ( θ T x ( i ) ) ∂ θ j = ∂ ( 1 + e − θ T x ( i ) ) ∂ θ j ( 1 + e − θ T x ( i ) ) 2 = − e − θ T x ( i ) x j ( i ) ( 1 + e − θ T x ( i ) ) 2 即 : ∂ g ( θ T x ( i ) ) ∂ θ j = h θ ( x ( i ) ) ( 1 − h θ ( x ( i ) ) ) x j ( i ) 代 入 ∂ J ( θ ) ∂ θ j 中 , 得 : θ j : = θ j − α m ∑ i = 1 m ( h θ ( x ( i ) ) − y ( i ) ) x j ( i ) \theta_j:=\theta_j-\frac{\alpha}{m}\frac{\partial}{\partial\theta_j}J(\theta) \\J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(h_\theta(x^{(i)}))+(1-y^{(i)})log(1-h_\theta(x^{(i)})) \\ J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}[y^{(i)}log(g(\theta^Tx^{(i)}))+(1-y^{(i)})log(1-g(\theta^Tx^{(i)})) \\ \frac{\partial J(\theta)}{\partial \theta_j}=-\frac{1}{m}\sum_{i=1}^{m}[\frac{y^{(i)}}{g(\theta^Tx^{(i)})}-(1-y^{(i)})\frac{1}{1-g(\theta^Tx^{(i)})}]\frac{\partial g(\theta^Tx^{(i)})}{\partial \theta_j} \\ 先求:\frac{\partial g(\theta^Tx^{(i)})}{\partial \theta_j}=\frac{\frac{\partial (1+e^{-\theta^Tx^{(i)}})}{\partial \theta_j}}{(1+e^{-\theta^Tx^{(i)}})^2}=-\frac{e^{-\theta^Tx^{(i)}}x_j^{(i)}}{(1+e^{-\theta^Tx^{(i)}})^2} \\即:\frac{\partial g(\theta^Tx^{(i)})}{\partial \theta_j}=h_\theta(x^{(i)})(1-h_\theta(x^{(i)}))x_j^{(i)} \\ 代入\frac{\partial J(\theta)}{\partial \theta_j}中,得:\theta_j:=\theta_j-\frac{\alpha}{m}\sum_{i=1}^{m}(h_\theta(x^{(i)})-y^{(i)})x_j^{(i)} θj:=θj−mα∂θj∂J(θ)J(θ)=−m1i=1∑m[y(i)log(hθ(x(i)))+(1−y(i))log(1−hθ(x(i)))J(θ)=−m1i=1∑m[y(i)log(g(θTx(i)))+(1−y(i))log(1−g(θTx(i)))∂θj∂J(θ)=−m1i=1∑m[g(θTx(i))y(i)−(1−y(i))1−g(θTx(i))1]∂θj∂g(θTx(i))先求:∂θj∂g(θTx(i))=(1+e−θTx(i))2∂θj∂(1+e−θTx(i))=−(1+e−θTx(i))2e−θTx(i)xj(i)即:∂θj∂g(θTx(i))=hθ(x(i))(1−hθ(x(i)))xj(i)代入∂θj∂J(θ)中,得:θj:=θj−mαi=1∑m(hθ(x(i))−y(i))xj(i)
4、sklearn实现逻辑回归
# -*- coding: utf-8 -*-
"""
Created on Tue Nov 12 19:28:12 2019
@author: 1
"""
from sklearn.model_selection import train_test_split
#导入logistics回归模型
from sklearn.linear_model import LogisticRegression
import numpy as np
import pandas as pd
df=pd.read_csv('D:\\workspace\\python\machine learning\\data\\breast_cancer.csv',sep=',',header=None,skiprows=1)
X = df.iloc[:,0:29]
y = df.iloc[:,30]
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LogisticRegression(solver='liblinear')
model.fit(X_train, y_train)
train_score = model.score(X_train, y_train)#R2值越接近1越好
cv_score = model.score(X_test, y_test)
print('train_score:{0:.6f}, cv_score:{1:.6f}'.format(train_score, cv_score))
y_pre = model.predict(X_test)
y_pre_proba = model.predict_proba(X_test)#输出概率
print('matchs:{0}/{1}'.format(np.equal(y_pre, y_test).shape[0], y_test.shape[0]))#shape[0]列,shape[1]行
#print('y_pre:{}, \ny_pre_proba:{}'.format(y_pre, y_pre_proba))#输出概率预测值
5、多分类问题
5.1多分类原理
为了实现多分类,我们将多个类(D)中的一个类标记为正向类(y=1),然后将其他所有类都标记为负向类,这个模型记作 h θ ( 1 ) ( X ) h_\theta^{(1)}(X) hθ(1)(X) 。接着,类似地第我们选择另一个类标记为正向类(y=2),再将其它类都标记为负向类,将这个模型记作 h θ ( 2 ) ( X ) h_\theta^{(2)}(X) hθ(2)(X) 依此类推。最后我们得到一系列的模型简记为:
h θ ( k ) ( X ) = P ( y = k ∣ X , θ ) h_\theta^{(k)}(X)=P(y=k|X,\theta) hθ(k)(X)=P(y=k∣X,θ)其中 k = 1 , 2 , . . . , D k=1,2,...,D k=1,2,...,D
最后,在做预测时,对每一个输入的测试变量,我们将所有的分类机都运行一遍,选择可能性最高的分类机的输出结果作为分类结果:
m a x h θ ( k ) ( x ( i ) ) max\;h_\theta^{(k)}(x^{(i)}) maxhθ(k)(x(i))
5.2sklearn实现多分类
# -*- coding: utf-8 -*-
"""
Created on Tue Nov 12 22:07:34 2019
@author: 1
"""
from sklearn.model_selection import train_test_split
#导入logistics回归模型
from sklearn.linear_model import LogisticRegression
from sklearn.metrics import accuracy_score
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib as mpl
df=pd.read_csv(r'D:\\workspace\\python\machine learning\\data\\iris.csv',sep=',')
X = df.iloc[:,0:2]
y = df.iloc[:,4]
x_train, x_test, y_train, y_test = train_test_split(X, y, test_size=0.2)
model = LogisticRegression(solver='liblinear')
model.fit(x_train, y_train)
y_pre = model.predict(x_test)
print('accuracy_score:{}'.format(accuracy_score(y_test,y_pre)))
y_pre_proba = model.predict_proba(x_test)
print('y_pre:{}, \ny_pre_proba:{}'.format(y_pre, y_pre_proba))#输出概率预测值
cm_dark = mpl.colors.ListedColormap(['g', 'r', 'b'])
plt.figure(1)
# 画原始数据图
colors = ['blue', 'red','green']
plt.subplot(1,2,1)
plt.scatter(x_test.iloc[:, 0], x_test.iloc[:, 1], c=y_test, cmap=cm_dark, marker='o', edgecolors='k')
plt.title('原始数据分类结果')
# 画分类结果图
plt.subplot(1,2,2)
plt.scatter(x_test.iloc[:, 0], x_test.iloc[:, 1], c=y_pre, cmap=cm_dark, marker='o', edgecolors='k')
plt.title('预测数据分类结果')
