时序分析(8) -- GARCH(p,q)模型

时序分析(8)

GARCH(p,q)模型

    上篇文章我们探讨了ARCH模型对时序数据的波动性进行建模和预测，本篇文章介绍GARCH模型。 首先我们介绍GARCH模型的基本概念：

Generalized Autoregressive Conditionally Heteroskedastic Models - GARCH(p,q)

简单来说，GARCH模型就是ARMA模型应用在时序的方差上，它包含一个自回归项和一个移动平均项.

如果时序数据$\{y_t\}$可以表示为
$$y_t={\sigma }_t{w}_t$$
其中$\{w_t\}$是高斯白噪声，均值为0，方差为1，这里${\sigma }_t$为
$${\sigma }_t^2={\alpha }_0+\sum _{i=1}^q{\alpha }_i{y}_{t-i}^2+\sum _{j=1}^p{\beta }_j{\sigma }_{t-j}^2$$
让我们先从简单做起，考虑GARCH(1,1)模型
$$y_t={\sigma }_t{w}_t$$
$${\sigma }_t^2={\alpha }_0+{\alpha }_1{y}_{t-1}^2+{\beta }_1{\sigma }_{t-1}^2$$
注意：这里${\alpha }_1+{\beta }_1<1$，否则时序将会不稳定。

导入python包和数据

如前一样

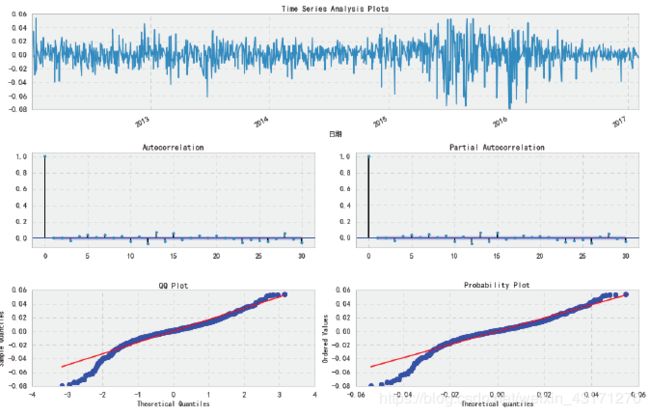
我们先模拟一个GARCH(1,1)时序

# Simulating a GARCH(1, 1) process
np.random.seed(2)

a0 = 0.2
a1 = 0.5
b1 = 0.3

n = 10000
w = np.random.normal(size=n)
y = np.zeros_like(w)
sigsq = np.zeros_like(w)

for i in range(1, n):
    sigsq[i] = a0 + a1*(y[i-1]**2) + b1*sigsq[i-1]
   y[i] = w[i] * np.sqrt(sigsq[i])
_ = tsplot(y, lags=30)

看上去很类似一个白噪声过程。

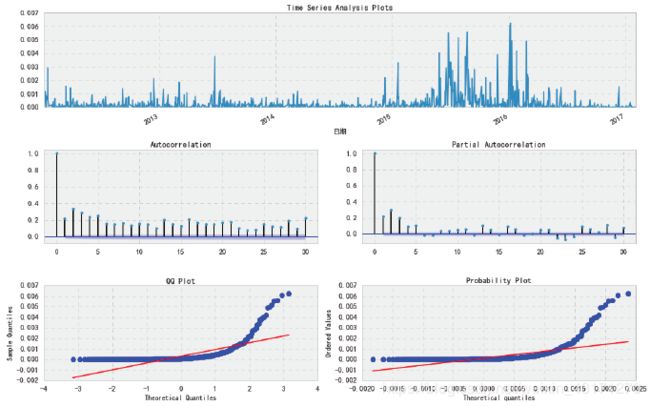
模拟时序的平方

tsplot(y*y, lags=30)

从ACF,PACF中显示出显著自相关性，我们需要AR项和MA项。
我们尝试是否可以通过模型拟合来得到模拟的参数。

# Fit a GARCH(1, 1) model to our simulated EPS series
# We use the arch_model function from the ARCH package
am = arch_model(y)
res = am.fit(update_freq=5)
print(res.summary())

我们较好地恢复了参数。

模拟数据GARCH残差plot

_ = tsplot(res.resid, lags=30)

以GARCH建模国内股票收益率

步骤如下：

1. 以ARIMA模型迭代得到最佳参数。
2. 以ARIMA模型所得到地具备最低AIC的参数来选择GARCH模型。
3. 使GARCH模型适配时序数据。
4. 检查模型残差和残差平方的自相关性。

def _get_best_model(TS):
    best_aic = np.inf
    best_order = None
    best_mdl = None
    pq_rng = range(5) # [0,1,2,3,4]
    d_rng = range(2) # [0,1]
    for i in pq_rng:
        for d in d_rng:
            for j in pq_rng:
                try:
                    tmp_mdl = smt.ARIMA(TS, order=(i,d,j)).fit(
                                       method='mle', trend='nc'
                              )
                    tmp_aic = tmp_mdl.aic
                    if tmp_aic < best_aic:
                        best_aic = tmp_aic
                        best_order = (i, d, j)
                        best_mdl = tmp_mdl
                 except: continue
                 
    print('aic: {:6.5f} | order: {}'.format(best_aic, best_order))
    return best_aic, best_order, best_mdl
# Notice I've selected a specific time period to run this analysis
TS = indexs_logret['国内股票']
res_tup = _get_best_model(TS)

aic: -6601.86081 | order: (3, 0, 2)
得到p,d,q = 3,0,2
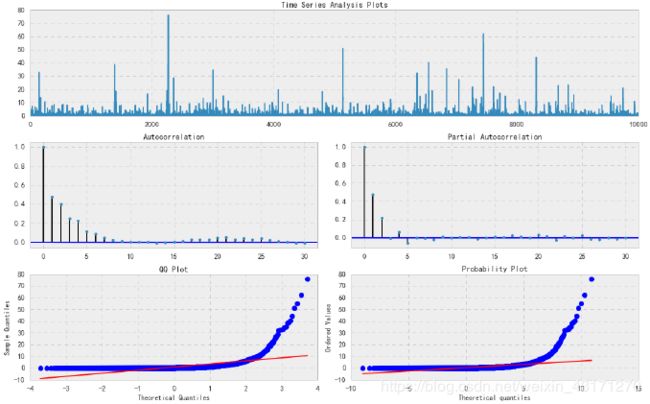
残差Plot

_ = tsplot(res_tup[2].resid, lags=30)

残差并非正态分布。

残差平方

_ = tsplot(res_tup[2].resid**2, lags=30)

残差平方显示较强的自相关性

拟合GARCH模型

order = [3,0,2]
p_ = order[0]
o_ = order[1]
q_ = order[2]

# Using student T distribution usually provides better fit
am = arch_model(10*TS, p=p_, o=o_, q=q_, dist='StudentsT')
res = am.fit(update_freq=5, disp='off')
print(res.summary())

GARCH模型残差Plot

_ = tsplot(res.resid, lags=30)

残差平方自相关性依然显著，说明模型拟合不是很成功。

香港股票收益率GARCH拟合

过程同上
aic: -1958.01617 | order: (2, 0, 2)
得到p,d,q=2,0,2
残差Plot

残差平方Plot

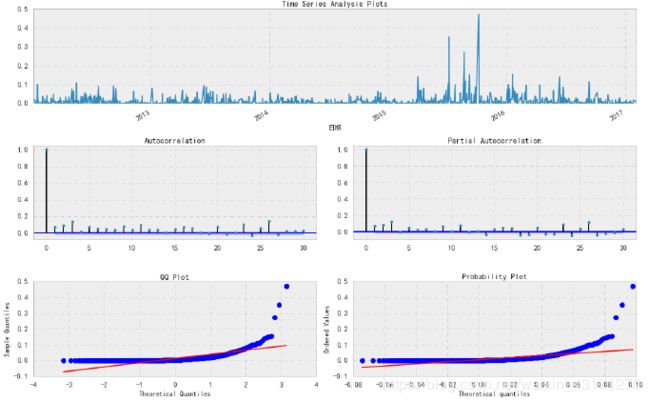
拟合GARCH模型

order = [2,0,2]
p_ = order[0]
o_ = order[1]
q_ = order[2]
# Using student T distribution usually provides better fit
am = arch_model(10*TS, p=p_, o=o_, q=q_, dist='StudentsT')
res = am.fit(update_freq=5, disp='off')
print(res.summary())

GARCH残差Plot

拟合效果优于国内股票

总结

    本文展示了采用Python语言为指数时序数据进行GARCH建模，并介绍了GARCH模型的基本概念。