圆弧和椭圆的扫描转换算法
文章目录
- 圆弧的扫描转换算法
- 一、 直接算法
- 二、角度DDA算法
- 三、中点算法
- 四、正负法
- 椭圆的扫描转换
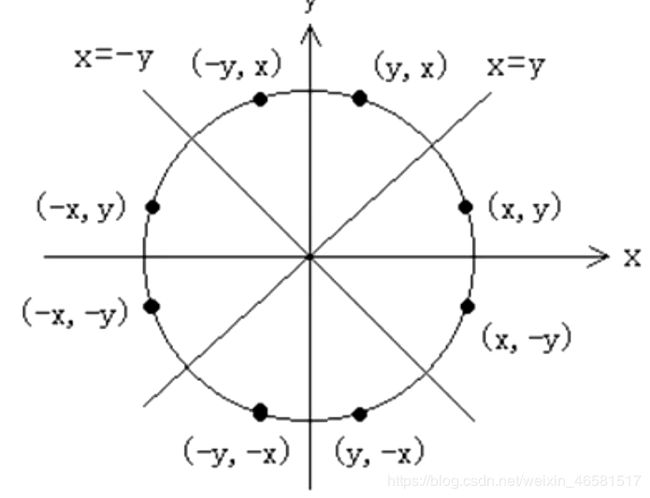
- 椭圆的对称性
- 中点算法
圆弧的扫描转换算法
一、 直接算法
两种直接离散方法:
- 利用隐函数方程: x 2 + y 2 = R 2 x^2 + y^2 = R^2 x2+y2=R2
( x i , y i = R 2 − x i 2 ) 取 整 > ( x i , y i , r ) (x_i, y_i = \sqrt{R^2 - x_i^2}) \frac{取整}{}>(x_i, y_{i,r}) (xi,yi=R2−xi2)取整>(xi,yi,r) - 利用参数方程: { x = R cos θ y = R sin θ \begin{cases}x = R\cos{\theta} \\ y = R\sin{\theta} \end{cases} {x=Rcosθy=Rsinθ
这两种方法都不可取,因为分别用到了开根运算、三角函数运算、浮点运算、取整等,计算量大,效率不高,不均匀。
二、角度DDA算法
由圆的参数方程:
{ x = R cos θ y = R sin θ \begin{cases} x = R\cos{\theta} \\ y = R\sin{\theta} \end{cases} {x=Rcosθy=Rsinθ
取微分:
{ d x = − R sin θ d θ d y = R cos θ d θ ⇒ { d x = − y d θ d y = x d θ \begin{cases} dx = -R\sin{\theta}d\theta \\ dy = R\cos{\theta}d\theta \end{cases} \Rightarrow \begin{cases} dx = -yd\theta \\ dy = xd\theta \end{cases} {dx=−Rsinθdθdy=Rcosθdθ⇒{dx=−ydθdy=xdθ

三、中点算法
利用圆的对称性,只须讨论 1 8 \frac{1}{8} 81圆。考虑第一象限内 x ∈ [ 0 , R 2 ] x \in[0, \frac{R}{\sqrt{2}}] x∈[0,2R]的圆弧:
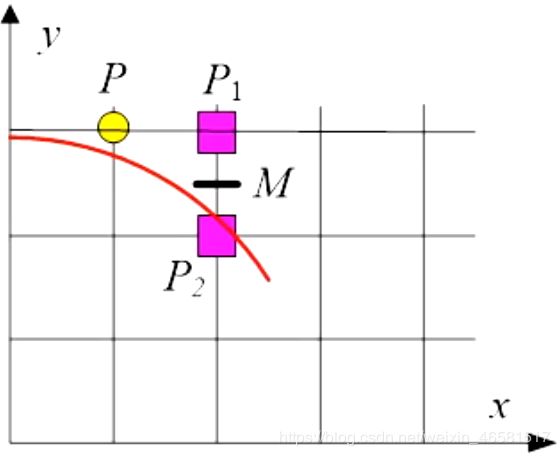
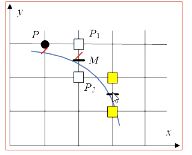
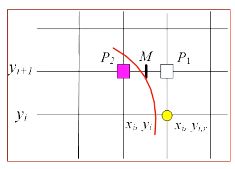
P ( x p , y p ) P(x_p,y_p) P(xp,yp)为当前点亮像素,那么下一个点亮的像素可能是 P 1 ( x p + 1 , y p ) P_1(x_p+1, y_p) P1(xp+1,yp)或 P 2 ( x p + 1 , y p − 1 ) P_2(x_p + 1, y_p - 1) P2(xp+1,yp−1)
- 设 M M M为 P 1 、 P 2 P_1、P_2 P1、P2间的中点, M = ( x p + 1 , y p + 0.5 ) M = (x_p + 1, y_p + 0.5) M=(xp+1,yp+0.5)
- 有如下结论:
-
F ( M ) < 0 → M F(M) < 0 \rightarrow M F(M)<0→M在圆内 → \rightarrow →取 P 1 P_1 P1
-
F ( M ) ≥ 0 → M F(M) \ge 0\rightarrow M F(M)≥0→M在圆外 → \rightarrow →取 P 2 P_2 P2
-
为此,可采用如下判别式:
d = F ( M ) = F ( x p + 1 , y p − 0.5 ) = ( x p + 1 ) 2 + ( y p − 0.5 ) 2 − R 2 d = F(M) = F(x_p + 1, y_p - 0.5) \\ \ \ = (x_p + 1)^2 + (y_p - 0.5)^2 - R^2 d=F(M)=F(xp+1,yp−0.5) =(xp+1)2+(yp−0.5)2−R2- (1) d < 0 d<0 d<0,则 P 1 P_1 P1为下一个像素,那么再下一个像素的判别式为: d 1 = F ( x p + 2 , y p − 0.5 ) = ( x p + 2 ) 2 + ( y p − 0.5 ) 2 − R 2 = d + 2 x p + 3 d_1 = F(x_p + 2, y_p - 0.5) \\ \qquad \qquad= (x_p+2)^2+(y_p-0.5)^2-R^2 \\ = d+ 2x_p + 3 d1=F(xp+2,yp−0.5)=(xp+2)2+(yp−0.5)2−R2=d+2xp+3
则 d d d的增量为 2 x p + 3 2x_p + 3 2xp+3
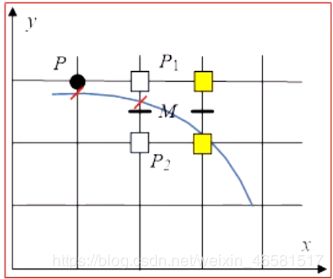
- (2) d ≥ 0 d \ge 0 d≥0,则 P 2 P_2 P2为下一个像素,那么在下一个像素的判别式为: d 1 = F ( x p + 2 , y p − 1.5 ) = ( x p + 2 ) 2 + ( y p − 1.5 ) 2 − R 2 = d + 2 ( x p − y p ) + 5 d_1 = F(x_p + 2, y_p - 1.5) \\ \qquad \qquad= (x_p+2)^2+(y_p-1.5)^2-R^2 \\ = d+ 2(x_p - y_p) + 5 d1=F(xp+2,yp−1.5)=(xp+2)2+(yp−1.5)2−R2=d+2(xp−yp)+5
即 d d d的增量为 2 ( x p − y p ) + 5 2(x_p - y_p) + 5 2(xp−yp)+5
d的初值: d 0 = F ( 1 , R − 0.5 ) = 1 + ( R − 0.5 ) 2 − R 2 = 1.25 − R d_0 = F(1, R - 0.5) = 1 + (R - 0.5)^2 - R^2 = 1.25 - R d0=F(1,R−0.5)=1+(R−0.5)2−R2=1.25−R
- (1) d < 0 d<0 d<0,则 P 1 P_1 P1为下一个像素,那么再下一个像素的判别式为: d 1 = F ( x p + 2 , y p − 0.5 ) = ( x p + 2 ) 2 + ( y p − 0.5 ) 2 − R 2 = d + 2 x p + 3 d_1 = F(x_p + 2, y_p - 0.5) \\ \qquad \qquad= (x_p+2)^2+(y_p-0.5)^2-R^2 \\ = d+ 2x_p + 3 d1=F(xp+2,yp−0.5)=(xp+2)2+(yp−0.5)2−R2=d+2xp+3
-
void MidpointCircle(int r, int color) {
int x, y;
float d;
x = 0; y = r; d = 1.25 - r;
drawpixel(x, y, color);
while (x < y) {
if ( d < 0 ) {
d += 2 * x + 3;
x++;
} else {
d += 2 * (x - y) + 5;
x++;
y--;
}
drawpixel(x, y, color);
}
}
四、正负法
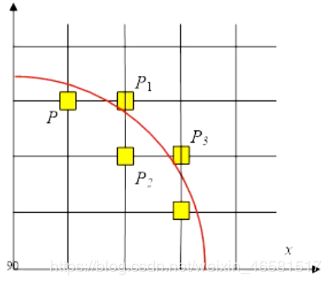
即求得 P i P_i Pi点后选择下一个像素点 P i + 1 P_{i+1} Pi+1的规则为:
- 当 F ( x i , y i ) ≤ 0 F(x_i, y_i) \leq 0 F(xi,yi)≤0,取 x i + 1 = x i + 1 , y i + 1 = y i x_{i+1} = x_i + 1,\ y_{i+1} = y_i xi+1=xi+1, yi+1=yi
F ( x i + 1 , y i + 1 ) = ( x i + 1 ) 2 + ( y i + 1 ) 2 − R 2 = ( x i + 1 ) 2 + y i 2 − R 2 = F ( x i , y i ) + 2 x i + 1 F(x_{i+1}, y_{i+1}) = (x_{i+1})^2 + (y_{i+1})^2 - R^2 \\ \qquad \qquad \quad \ \ \ = (x_i+1)^2 + y_i^2 - R^2 \\ \qquad \qquad \quad \ \ \ =F(x_i,y_i)+2x_i + 1 F(xi+1,yi+1)=(xi+1)2+(yi+1)2−R2 =(xi+1)2+yi2−R2 =F(xi,yi)+2xi+1 - 当 F ( x i , y i ) > 0 F(x_i, y_i) > 0 F(xi,yi)>0,取 x i + 1 = x i , y i + 1 = y i − 1 x_{i+1} = x_i,\ y_{i+1} = y_i - 1 xi+1=xi, yi+1=yi−1
F ( x i + 1 , y i + 1 ) = ( x i + 1 ) 2 + ( y i + 1 ) 2 − R 2 = x i 2 + ( y i − 1 ) 2 − R 2 = F ( x i , y i ) − 2 y i + 1 F(x_{i+1}, y_{i+1}) = (x_{i+1})^2 + (y_{i+1})^2 - R^2 \\ \qquad \qquad \quad \ \ \ = x_i^2 + (y_i - 1)^2 - R^2 \\ \qquad \qquad \quad \ \ \ =F(x_i,y_i)-2y_i + 1 F(xi+1,yi+1)=(xi+1)2+(yi+1)2−R2 =xi2+(yi−1)2−R2 =F(xi,yi)−2yi+1
椭圆的扫描转换
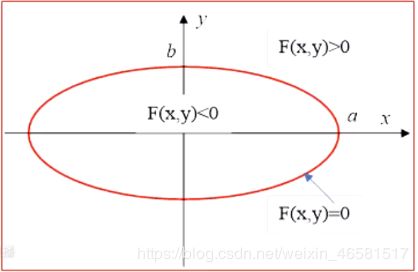
- 标准椭圆方程: x 2 a 2 + y 2 b 2 = 1 \frac{x^2}{a^2} + \frac{y^2}{b^2} = 1 a2x2+b2y2=1
- 隐函数的形式: F ( x , y ) = ( b x ) 2 + ( a y ) 2 − ( a b ) 2 = 0 F(x,y) = (bx)^2 + (ay)^2 - (ab)^2 = 0 F(x,y)=(bx)2+(ay)2−(ab)2=0
椭圆的对称性
- 椭圆的对称性,只考虑第一象限跟随椭圆弧的生成,分上下两部分,以切线斜率为-1的点( P )作为分界点。
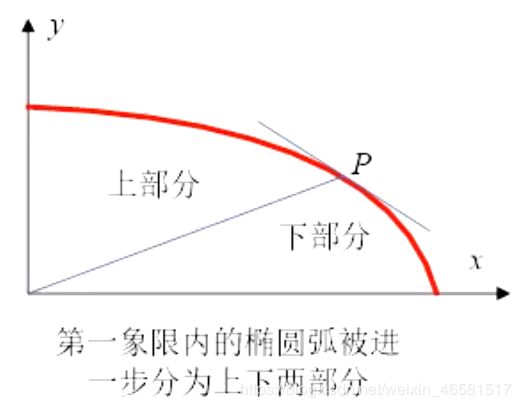
- 椭圆上任一点 ( x , y ) (x,y) (x,y)处的法向量为: ( ∂ F ∂ x , ∂ F ∂ y ) = ( 2 b 2 x , 2 a 2 y ) (\frac{\partial{F}}{\partial{x}},\frac{\partial{F}}{\partial{y}}) = (2b^2x,2a^2y) (∂x∂F,∂y∂F)=(2b2x,2a2y)
P点处的两个分量相等,即: 2 b 2 x = 2 a 2 y 2b^2x = 2a^2y 2b2x=2a2y
中点算法
确定一个像素后,接着在两个候选像素的中点计算一个判别式的值,由判别式的符号确定更近的点。
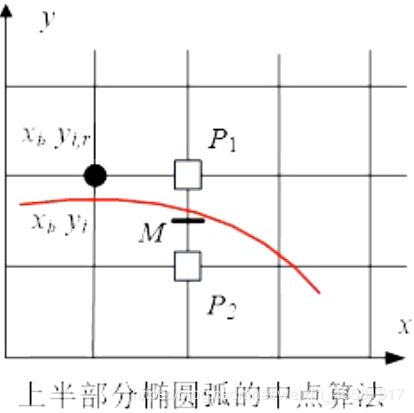
- 椭圆弧的上部分,各点斜率在 [ − 1 , 0 ] [-1, 0] [−1,0]之间
设 ( x p , y p ) (x_p,y_p) (xp,yp)已确定,则下一待选像素的中点 M M M是 ( x p + 1 , y p − 0.5 ) (x_p + 1, y_p - 0.5) (xp+1,yp−0.5)
d 1 = F ( x p + 1 , y p − 0.5 ) = b 2 ( x p + 1 ) 2 + a 2 ( y p − 0.5 ) 2 − a 2 b 2 d_1 = F(x_p+1, y_p-0.5) = b^2(x_p+1)^2 + a^2(y_p - 0.5)^2 - a^2b^2 d1=F(xp+1,yp−0.5)=b2(xp+1)2+a2(yp−0.5)2−a2b2
- 再讨论椭圆弧的下部分,各点斜率 k k k满足: 1 k ∈ [ − 1 , 0 ] \frac{1}{k}\in[-1,0] k1∈[−1,0]
MidPointEllipe(int a, int b, int color) {
int x, y;
float d1, d2;
x = 0,; y = b;
d1 = b * b + a * a * (-b + 0.25); // 初始判别式
putpixel(x, y, color);
while (b * b * (x + 1) < a * a * (y - 0.5)) { // 椭圆的上部
if (d1 < 0) {
d1 += b * b * (2 * x + 3);
x++;
} else {
d1 += (b * b * (2 * x + 3) + a * a * (-2 * y + 2));
x++;
y--;
}
putpixel(x, y, color);
} // 上部分
d2 = sqr(b * (x + 0.5)) + sqr(a * (y - 1)) - sqr(a * b);
while (y > 0) {
if (d2 < 0) {
d2 += b * b * (2 * x + 2) + a * a * (-2 * y + 3);
x++;
y--;
} else {
d2 += a * a * (-2 * y + 3);
y--;
}
putpixel(x, y, color);
}
}