wonner_

竞赛常用集成学习框架Boosting算法总结(XGBoost、LightGBM)(附代码)

Boosting类算法简介

Boosting是一类可将弱学习器提升为强学习器的算法，这类算法的工作机制如下：先从初始训练集训练出一个基学习器，再根据基学习器的表现对训练样本分布进行调整，使得先前基学习器做错的训练样本在后续受到更多关注，然后基于调整后的样本分布来训练下一个基学习器；重复进行这一操作，最终将各个基学习器得到的结果加权结合。常见的Boosting算法包括GBDT、XGBoost和LightGBM等。

XGBoost

XGBoost原理

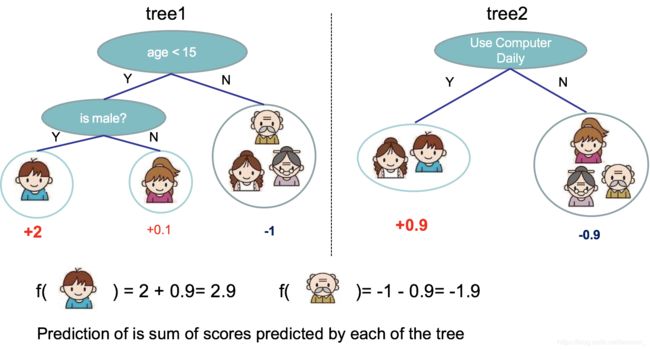
XGBoost是由K个基模型组成的一个加法运算式，其基模型为CART回归树（二叉树）。训练完成得到K棵树，当预测一个样本的分数时，根据这个样本的特征，在每棵树中会落到对应的一个叶子节点，每个叶子节点对应一个分数，将每棵树对应的分数加起来就是该样本的预测值。

$\hat{y}_{i}=\sum_{k=1}^{K} f_{k}\left(x_{i}\right)$

如下图例子，训练两棵决策树，小孩的预测分数就是两棵树中小孩所落到的结点的分数相加。爷爷的预测分数同理。

XGBoost的目标函数定义为：

$O b j=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}\right)+\sum_{k=1}^{K} \Omega\left(f_{k}\right)$ 其中 $\Omega\left(f_{t}\right)=\gamma T+\frac{1}{2} \lambda \sum_{j=1}^{T} w_{j}^{2}$

目标函数由两部分构成，第一部分用来衡量预测分数和真实分数的差距，第二部分为正则化项。正则化项同样包含两部分，T表示叶子结点的个数，w表示叶子节点的分数。超参数γ可以控制叶子结点的个数，λ可以控制叶子节点的分数不会过大，防止树过于复杂而造成过拟合。

boosting 模型是前向加法，第t步的模型拟合上次预测的残差，即：

$\hat{y}_{i}^{t}=\hat{y}_{i}^{t-1}+f_{t}\left(x_{i}\right)$

此时，目标函数可改写为：

$O b j^{(t)}=\sum_{i=1}^{n} l\left(y_{i}, \hat{y}_{i}^{(t-1)}+f_{t}\left(x_{i}\right)\right)+\Omega\left(f_{t}\right)$

以平方误差为例，将上式进行二阶泰勒展开得：

$O b j^{(t)} \simeq \sum_{i=1}^{n}\left[l\left(y_{i}, \hat{y}_{i}^{(t-1)}\right)+g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

其中 $g_{i}=\partial_{\hat{y}^{(t-1)}}\left(\hat{y}^{(t-1)}-y_{i}\right)^{2}=2\left(\hat{y}^{(t-1)}-y_{i}\right) \quad$ $h_{i}=\partial_{\hat{y}^{(t-1)}}^{2}\left(y_{i}-\hat{y}^{(t-1)}\right)^{2}=2$

目标函数第一项为常数，对优化不影响，可以直接去掉，此时，目标函数简化为：

$O b j^{(t)}=\sum_{i=1}^{n}\left[g_{i} f_{t}\left(x_{i}\right)+\frac{1}{2} h_{i} f_{t}^{2}\left(x_{i}\right)\right]+\Omega\left(f_{t}\right)$

我们知道，每个样本都最终会落到一个叶子结点中，所以可将 $f_{t}\left(x_{i}\right)$ 替换为其落入的叶子节点的分数w，将树的正则化一并整理到式中得到：

$O b j^{(t)}=\sum_{j=1}^{T}\left[\left(\sum_{i \in I_{j}} g_{i}\right) w_{j}+\frac{1}{2}\left(\sum_{i \in I_{j}} h_{i}+\lambda\right) w_{j}^{2}\right]+\gamma T$

此时目标函数是关于叶子结点分数w的一个一元二次函数，求解最优的w和和其对应的最优目标函数值如下：

$w_{j}^{*}=-\frac{G_{j}}{H_{j}+\lambda}$ $O b j=-\frac{1}{2} \sum_{j=1}^{T} \frac{G_{j}^{2}}{H_{j}+\lambda}+\gamma T$

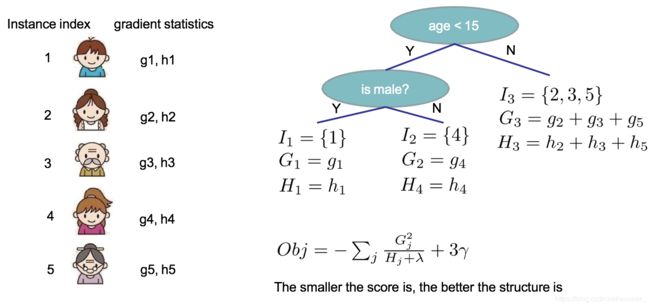
根据下图举例说明叶子节点的分数w如何计算。每个叶子节点的G和H将落入其中的样本求和，再根据上文给出的公式求得分数。

在上面的推导中，我们知道了如果我们一棵树的结构确定了，如何求得每个叶子结点的分数。下面介绍如何确定树的结构。

XGBoost使用了和CART回归树一样的想法，可利用贪婪算法，遍历所有特征的内部的所有划分点，不同的是使用上式目标函数值作为评价函数。可利用近似算法，对于连续型特征，根据分位数对特征进行分桶，即找到m个划分点，可以在生成一颗树之前对特征做好划分（全局），也可以在分裂叶子节点时计算划分（局部）。根据目标函数值计算节点分裂的增益，使用增益最大的特征及划分点进行分裂。同时为了限制树生长过深，加入阈值(gamma)限制，只有当增益大于该阈值才进行分裂。当特征值缺失时，XGBoost的思想是将该样本分别划分到左结点和右结点，然后计算其增益，哪个大就划分到哪边。

此外，XGBoost使用了Shrinkage方法，相当于学习速率(learning_rate,eta)。XGBoost 在进行完一次迭代后，会将叶子节点的权重乘上该系数，主要是为了削弱每棵树的影响，让后面有更大的学习空间；

$\hat{y}_{i}^{t}=\hat{y}_{i}^{t-1}+\eta f_{t}\left(x_{i}\right)$

XGBoost基模型为回归树，是如何适用于分类问题的呢？它将每个样本计算得到的分数经过一个变化转化为该样本属于该类的概率，那么每轮拟合的残差即为输入样本对应某类的真实概率（1或0）- 前面k-1棵树组合计算的对应该类的概率值。对于多分类问题，为每个类别分别建树，也就是说，对于一个k分类问题，总共建树数量为k*n_estimator。

XGBoost是如何并行训练的？XGBoost的并行，并不是说每棵树可以并行训练，XGB本质上仍然采用boosting思想，每棵树训练前需要等前面的树训练完成才能开始训练。XGBoost的并行，指的是特征维度的并行：决策树的学习最耗时的一个步骤就是在每次寻找最佳分裂点是都需要对特征的值进行排序。而 XGBoost 在训练之前对根据特征对数据进行了排序，然后保存到块结构中。在对节点进行分裂时需要选择增益最大的特征作为分裂，这时各个特征的增益计算可以同时进行。

XGBoost使用特征重要性进行特征选择

使用XGBoost训练模型可以自动地获取特征的重要性，从而有效地进行特征的筛选。特征的重要性表示这个特征在构建提升树的作用。去除一些不重要的特征可能会使模型准确率提高，因为这些特征可能是噪声。

xgboost内置了get_fscore函数获取特征重要性，API如下：

get_score(fmap='', importance_type='weight')

获取每个特征的特征重要性，有以下几种度量方式：

‘weight’: 特征作为分裂节点的次数
‘total_gain’: 某特征在每次分裂节点时带来的总增益
‘total_cover’: 某特征在每次分裂节点时处理的样本的数量之和
‘gain’: total_gain/weight
‘cover’: total_cover/weight

此外，通过XGBoost model参数也可指定特征重要性度量方式(importance_type:默认为'gain')，通过model属性feature_impoerance_获得特征重要性。通过对特征重要性进行排序，逐个剔除不重要的特征，查看剔除特征后模型效果的提升情况来选择留下哪些特征。本文以多分类问题为例，给出使用交叉验证进行特征选择的代码。

import numpy as np 
import pandas as pd 

import xgboost as xgb
from xgboost.sklearn import XGBClassifier
from sklearn.model_selection import GridSearchCV
from sklearn.metrics import cohen_kappa_score, make_scorer
from sklearn.feature_selection import SelectFromModel

new_train = pd.read_csv('/kaggle/input/dataset/train_feature.csv')

train_x = new_train.drop(['accuracy_group'],axis=1).values
train_y = new_train['accuracy_group'].values

model_xgb = XGBClassifier(
        learning_rate =0.1,  # 学习率
        n_estimators=1000,   # 树的个数
        max_depth=5,         # 树的最大深度
        min_child_weight=1,  # 叶子节点样本权重加和最小值sum(H)
        gamma=0,             # 节点分裂所需的最小损失函数下降值
        subsample=0.8,       # 样本随机采样作为训练集的比例
        colsample_bytree=0.8, # 使用特征比例
        objective= 'multi:softmax', # 损失函数(这里为多分类）
        num_class=4,         # 多分类问题类别数
        scale_pos_weight=1,  # 类别样本不平衡
        seed=1)

# 使用默认参数训练一个模型以得到特征重要性
model_xgb.fit(train_x,train_y)

thresholds = np.sort(model_xgb.feature_importances_)
xgb_param = model_xgb.get_xgb_params()
for thresh in thresholds:
    # select features using threshold
    selection = SelectFromModel(model_xgb, threshold=thresh, prefit=True)
    select_train_x = selection.transform(train_x)
    # 5折交叉验证
    xgtrain = xgb.DMatrix(select_train_x, label=train_y)
    cvresult = xgb.cv(xgb_param,xgtrain,num_boost_round=xgb_param['n_estimators'],             
                       nfold=5,metrics='mlogloss', early_stopping_rounds=50)
    score = cvresult['test-mlogloss-mean'].iloc[-1]
    print("Thresh=%.3f, n=%d, Accuracy: %.2f%%" % (thresh, select_train_x.shape[1], score))

XGBoost使用K折交叉验证 + 网格搜索(Grid Search)调参

本文参考XGBoost参数调优完全指南（附Python代码），使用grid search对模型参数分组调优。由于XGBoost的参数过多，所有参数一起调网格搜索空间太大，因此将参数分成几组分别调优。关于XGBoost的参数在链接文章中已经给出了详细的描述，故本文不再赘述。只是修改了上文中的部分代码以适应XGBoost版本更新带来的变化，并将参数调节的几个步骤整理在一起，实现自动调参。

# step1:初始使用一个较大的学习速率，其他参数使用初始估计值，确定当前最佳决策树数量
xgb_param = model_xgb.get_xgb_params()
xgtrain = xgb.DMatrix(train_x, label=train_y)
cvresult = xgb.cv(xgb_param, xgtrain, num_boost_round=xgb_param['n_estimators'], nfold=5,
                metrics='mlogloss', early_stopping_rounds=50)
# 根据交叉验证结果修改决策树的个数
model_xgb.set_params(n_estimators=cvresult.shape[0])

# step2：max_depth 和 min_weight 粗调优
param_test = {
 'max_depth':range(3,10,2),
 'min_child_weight':range(1,8,2)
}
gsearch = GridSearchCV(estimator=model_xgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
gsearch.fit(train_x,train_y)
print(gsearch.best_score_)
curr_max_depth = gsearch.best_params_['max_depth']
curr_min_child_weight = gsearch.best_params_['min_child_weight']

# step3: 根据上一步的结果对max_depth 和 min_weight 精调优 在step2最优值上下范围各扩展1
param_test = {
 'max_depth':[curr_max_depth-1,curr_max_depth,curr_max_depth+1],
 'min_child_weight':[curr_min_child_weight-1,curr_min_child_weight,curr_min_child_weight+1]
}
gsearch = GridSearchCV(estimator=model_xgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
gsearch.fit(train_x,train_y)
print(gsearch.best_score_)
model_xgb.set_params(max_depth=gsearch.best_params_['max_depth'])
model_xgb.set_params(min_child_weight=gsearch.best_params_['min_child_weight'])

# step4: gamma调优
param_test = {
 'gamma':[i/10.0 for i in range(0,5)]
}
gsearch = GridSearchCV(estimator=model_xgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
gsearch.fit(train_x,train_y)
print(gsearch.best_score_)
model_xgb.set_params(gamma=gsearch.best_params_['gamma'])

# step5: 调整subsample 和 colsample_bytree 参数
param_test = {
 'subsample':[i/10.0 for i in range(6,10)],
 'colsample_bytree':[i/10.0 for i in range(6,10)]
}
gsearch = GridSearchCV(estimator=model_xgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
gsearch.fit(train_x,train_y)
print(gsearch.best_score_)
model_xgb.set_params(subsample=gsearch.best_params_['subsample'])
model_xgb.set_params(colsample_bytree=gsearch.best_params_['colsample_bytree'])

# step6: 正则化参数以及其他未给出初始定义的参数调优，要注意加入这些参数后模型效果是否变好

# step7: 使用上述调优后的参数 降低学习率并调优增加决策树个数
model_xgb.set_params(learning_rate=0.01)
cvresult = xgb.cv(model_xgb.get_xgb_params(), xgtrain, num_boost_round=1000, nfold=5,
                metrics='mlogloss', early_stopping_rounds=50)
# 根据交叉验证结果修改决策树的个数
model_xgb.set_params(n_estimators=cvresult.shape[0])

XGBoost原理部分参考内容：

【机器学习】决策树（下）——XGBoost、LightGBM（非常详细）

一文读懂机器学习大杀器XGBoost原理

陈天奇 xgboost ppt 密码：v3y6

LightGBM

LightGBM原理

LightGBM 由微软提出，主要用于解决 GDBT 在海量数据中遇到的问题。GBDT在每一次迭代的时候，都需要遍历整个训练数据多次。如果把整个训练数据装进内存则会限制训练数据的大小；如果不装进内存，反复地读写训练数据又会消耗非常大的时间。尤其面对工业级海量的数据，普通的GBDT算法是不能满足其需求的。LightGBM相对XGBoost 具有训练速度快、内存占用低的特点。为了达到这两点，LightGBM提出了以下几点解决方案。包括1-2两个大的优化和剩余的一些小的优化。

单边梯度抽样算法(Gradient-based One-Side Sampling, GOSS)；
互斥特征捆绑算法(Exclusive Feature Bundling, EFB)；
直方图算法；
基于最大深度的 Leaf-wise 的垂直生长算法；
类别特征最优分割；

单边梯度抽样算法

GBDT 算法的梯度大小可以反应样本的权重，梯度越小说明模型拟合的越好，单边梯度抽样算法（Gradient-based One-Side Sampling, GOSS）利用这一信息对样本进行抽样，减少了大量梯度小的样本，在接下来的计算中只需关注梯度高的样本，极大的减少了计算量。用梯度描述可能不够直观，我们知道boosting模型是前向加法，第t步的模型拟合上次预测的残差，在GDBT中残差其实是最小均方损失函数关于预测值的反向梯度，也就是说，预测值和实际值的残差与损失函数的负梯度相同。我们可以近似的理解为，在接下来的计算中更多关注预测值与实际值偏差较大的样本。

GOSS算法保留了梯度大的样本，将更多的注意力放在训练不足的样本上；而为了不改变样本的数据分布，对梯度小的样本进行随机抽样，并引入一个常数进行平衡。GOSS首先根据数据的梯度绝对值排序，选取a%个实例。然后在剩余的数据中随机采样b%个实例。接着计算信息增益时为采样出的小梯度数据乘以(1-a)/b进行放大。

互斥特征捆绑算法

这一算法用来减少特征的数量。高维特征往往是稀疏的，而且特征间可能是相互排斥的（如两个特征不同时取非零值），如果两个特征并不完全互斥（如只有一部分情况下是不同时取非零值），可以用互斥率表示互斥程度。互斥特征捆绑算法（Exclusive Feature Bundling, EFB）指出如果将一些特征进行融合绑定，则可以降低特征数量。

1. 哪些特征可以一起绑定？

EFB 算法利用特征和特征间的关系构造一个加权无向图，顶点是特征，边是两个特征间互斥程度；

根据节点的度进行降序排序，度越大，与其他特征的冲突越大；

检查排序之后的每个特征，对他进行特征绑定bundle或者建立新的绑定bundle使得操作之后的总体冲突最小。

2. 特征绑定后，特征值如何确定？

如何合并同一个bundle的特征来降低训练时间复杂度。关键在于原始特征值可以从bundle中区分出来。假设 Bundle 中有两个特征值，A 取值为 [0, 10]、B 取值为 [0, 20]，为了保证特征 A、B 的互斥性，我们可以给特征 B 添加一个偏移量转换为 [10, 30]，Bundle 后的特征其取值为 [0, 30]，这样便实现了特征合并。

直方图算法

直方图算法的基本思想是将连续的特征离散化为 k 个离散特征，同时构造一个宽度为 k 的直方图用于统计信息（含有 k 个 bin）。利用直方图算法我们无需遍历数据，只需要遍历 k 个 bin 即可找到最佳分裂点。这个思想和XGBoost中分裂树节点使用的近似算法类似，但 XGBoost在每一层都动态的重新构建直方图，而LightGBM中对每个特征都有一个直方图，所以构建一次直方图就够了。

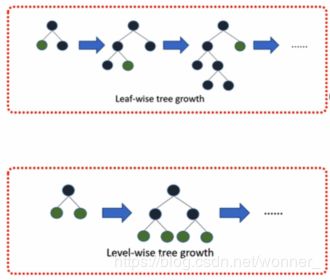
基于最大深度的 Leaf-wise 的垂直生长算法

在建树的过程中有两种策略：

Level-wise：基于层进行生长，直到达到停止条件；
Leaf-wise：每次分裂增益最大的叶子节点，直到达到停止条件。

XGBoost 采用 Level-wise 的增长策略，方便并行计算每一层的分裂节点，提高了训练速度，但同时也因为节点增益过小增加了很多不必要的分裂，增加了计算量；LightGBM 采用 Leaf-wise 的增长策略减少了计算量，配合最大深度的限制防止过拟合，由于每次都需要计算增益最大的节点，所以无法并行分裂。

类别特征最优分割

大部分的机器学习算法都不能直接支持类别特征（如XGBoost），一般都会对类别特征进行编码，然后再输入到模型中。常见的处理类别特征的方法为 one-hot 编码。这不仅降低了空间和时间的效率而且可能会影响决策树学习。所以LightGBM优化了对类别特征的支持，可以直接输入类别特征，不需要将其转化为数值特征。

LightGBM使用K折交叉验证 + 网格搜索(Grid Search)调参

LightGBM调参仍然使用与XGBoost一样的思路，但LightGBM加入了一些参数，且有些参数不同名但代表同一个意义。另外LightGBM中加入了类别变量，训练的时候可选择。

model_lgb = lgb.LGBMClassifier(
            learning_rate=0.1,   # 学习率
            n_estimators=1000,    # 树的个数
            max_depth=10,         # 树的最大深度
            num_leaves=31,        # 叶子节点个数 'leaf-wise'
            min_split_gain=0，    # 节点分裂所需的最小损失函数下降值
            objective='multiclass', # 多分类
            metric='multiclass',  # 评价函数
            num_class=4,          # 多分类问题类别数
            subsample=0.8,        # 样本随机采样作为训练集的比例
            colsample_bytree=0.8, # 使用特征比例
            seed=1)

# lightgbm 5折交叉验证 + 网格搜索(Grid Search)调参
def lgb_auto_para_tuning(model_lgb,train_x,train_y,categorical_feature):
    # step1:初始使用一个较大的学习速率，其他参数使用初始估计值，确定当前最佳决策树数量
    lgb_param = model_lgb.get_params()
    data_train = lgb.Dataset(train_x,train_y,categorical_feature=categorical_feature)
    cvresult = lgb.cv(lgb_param, data_train, categorical_feature=categorical_feature,num_boost_round=xgb_param['n_estimators'], nfold=5,
                    metrics='mlogloss', early_stopping_rounds=50)
    # 根据交叉验证结果修改决策树的个数
    model_lgb.set_params(n_estimators=cvresult.shape[0])
    print(model_lgb.get_params()['n_estimators'])
    
    # 类别变量
    train_x[categorical_feature] = train_x[categorical_feature].astype('category')
    # step2：max_depth 和 num_leaves 粗调优
    param_test = {
     'max_depth':range(3,10,2),
     'num_leaves':range(31,128,32)
    }
    gsearch = GridSearchCV(estimator=model_lgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
    gsearch.fit(train_x,train_y)
    print(gsearch.best_params_)     
    print(gsearch.best_score_)
    curr_max_depth = gsearch.best_params_['max_depth']
    curr_num_leaves = gsearch.best_params_['num_leaves']

    # step3: 根据上一步的结果对max_depth 和 num_leaves 精调优 在step2最优值上下范围各扩展1
    param_test = {
     'max_depth':[curr_max_depth-1,curr_max_depth,curr_max_depth+1],
     'num_leaves':[curr_num_leaves-8,curr_num_leaves,curr_num_leaves+8]
    }
    gsearch = GridSearchCV(estimator=model_lgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
    gsearch.fit(train_x,train_y)
    print(gsearch.best_params_)     
    print(gsearch.best_score_)
    model_xgb.set_params(max_depth=gsearch.best_params_['max_depth'])
    model_xgb.set_params(num_leaves=gsearch.best_params_['num_leaves'])

    # step4: min_split_gain调优
    param_test = {
     'min_split_gain':[i/10.0 for i in range(0,5)]
    }
    gsearch = GridSearchCV(estimator=model_lgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
    gsearch.fit(train_x,train_y)
    print(gsearch.best_params_)     
    print(gsearch.best_score_)
    model_xgb.set_params(min_split_gain=gsearch.best_params_['min_split_gain'])

    # step5: 调整subsample 和 colsample_bytree 参数
    param_test = {
     'subsample':[i/10.0 for i in range(6,10)],
     'colsample_bytree':[i/10.0 for i in range(6,10)]
    }
    gsearch = GridSearchCV(estimator=model_lgb,param_grid=param_test,scoring='accuracy',n_jobs=-1,cv=5)
    gsearch.fit(train_x,train_y)
    print(gsearch.best_params_)     
    print(gsearch.best_score_)
    model_xgb.set_params(subsample=gsearch.best_params_['subsample'])
    model_xgb.set_params(colsample_bytree=gsearch.best_params_['colsample_bytree'])

    # step6: 正则化参数以及其他未给出初始定义的参数调优，要注意加入这些参数后模型效果是否变好

    # step7: 使用上述调优后的参数 降低学习率并调优增加决策树个数
    model_lgb.set_params(learning_rate=0.01)
    cvresult = lgb.cv(model_lgb.get_xgb_params(), data_train,categorical_feature=categorical_feature,num_boost_round=1000, nfold=5,
                    metrics='mlogloss', early_stopping_rounds=50)
    # 根据交叉验证结果修改决策树的个数
    model_lgb.set_params(n_estimators=cvresult.shape[0])
    print(model_xgb.get_params()['n_estimators'])

LightGBM原理部分参考内容：