大话数据结构—多路查找树（B树）

　　多路查找树(muitl-way search tree)，其每一个节点的孩子数可以多于两个，且每一个节点处可以存储多个元素。主要有4中特殊形式。

---

一、2-3树

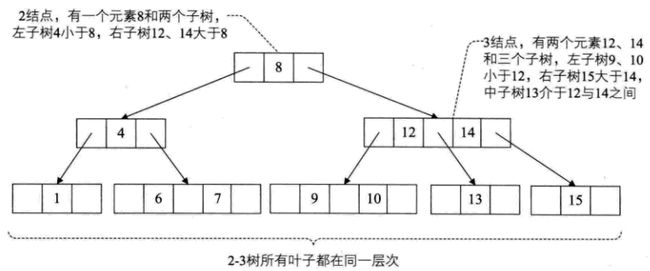
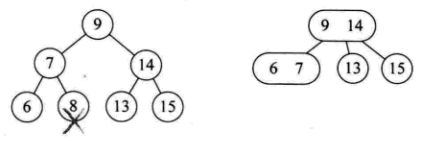
定义：其中的每一个节点都具有两个孩子（称为2节点）或者三个孩子（称为3节点）。
并且2-3树中所有的叶子都在同一层上。

一个2节点包含一个元素和两个孩子（或者没有孩子）。

一个3节点包含一小一大两个元素和三个孩子（或者没有孩子）。

1. 2-3树的插入实现

1）对于空树，插入一个2节点即可；

2）插入节点到一个2节点的叶子上。由于本身就只有一个元素，所以只需要将其升级为3节点即可。

3）插入节点到一个3节点的叶子上。因为3节点本身最大容量，因此需要拆分，且将树中两元素或者插入元素的三者中选择其一向上移动一层。
三种情况：

• 升级父节点
  

• 升级根节点
  

• 增加树高度
  

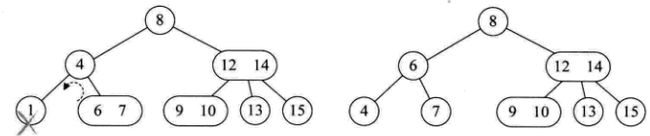
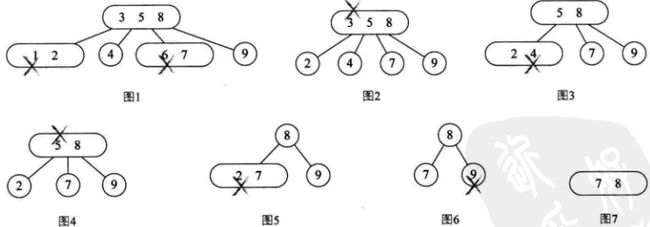
2. 2-3树的删除实现

1）所删元素位于一个3节点的叶子节点上，直接删除，不会影响树结构。

2）所删元素位于一个2节点上，直接删除，破坏树结构。

分为四种情况：

• 此节点双亲也是2节点，且拥有一个3节点的右孩子；
  

• 此节点的双亲是2节点，它右孩子也是2节点；
  

• 此节点的双亲是3节点；
  

• 当前树是一个满二叉树，降低树高；
  

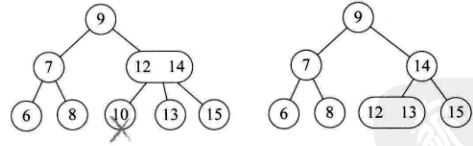
3）所删元素位于非叶子的分支节点。此时按树中序遍历得到此元素的前驱或后续元素，补位。

• 分支节点是2节点
  

• 分支节点是3节点
  

二、2-3-4树

2-3-4树是2-3树的扩展，包括了4节点的使用，一个4节点包含小中大三个元素和四个孩子（或没有孩子）。

1. 2-3-4树插入实现

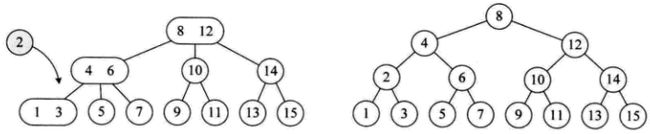
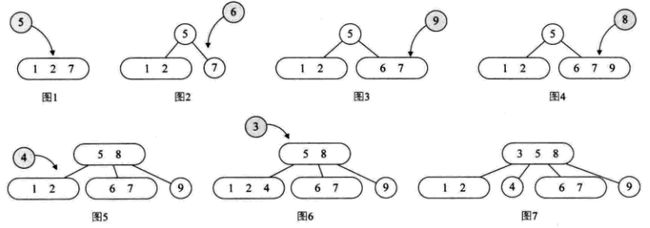
构建一个数组为{7,1,2,5,6,9,8,4,3}的2-3-4树的过程

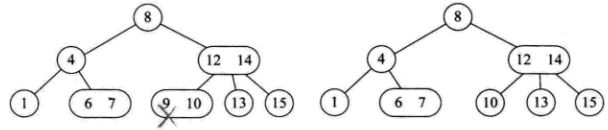
2. 2-3-4树删除实现

删除顺序使1,6,3,4,5,2,9

三、B树（B-树）

　　B树（B-树）是一种平衡的多路查找树。2-3树和2-3-4树都是B树的特例。节点最大的孩子数组称为B树的阶（order），因此，2-3树是3阶B树，2-3-4树是4阶B树。

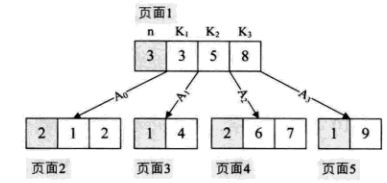
比如说要查找7，首先从外存读取得到根节点3,5,8三个元素，发现7不在，但是5、8之间，因此就通过A2再读取外存的6,7节点找到结束。

B树的插入和删除和2-3树、2-3-4树类似。

B树的数据结构为内外存的数据交互准备的。当要处理的数据很大时，无法一次全部装入内存。这时对B树调整，使得B树的阶数与硬盘存储的页面大小相匹配。比如说一棵B树的阶为1001（即1个节点包含1000个关键字），高度为2（从0开始），它可以存储超过10亿个关键字（1001x1001x1000+1001x1000+1000）,只要让根节点持久的保留在内存中，那么在这颗树上，寻找某一个关键字至多需要两次硬盘的读取即可。

对于n个关键字的m阶B树，最坏情况查找次数计算
第一层至少1个节点，第二层至少2个节点，由于除根节点外每个分支节点至少有⌈m/2⌉棵子树，则第三层至少有2x⌈m/2⌉个节点。。。这样第k+1层至少有2x(⌈m/2⌉)^(k-1),实际上，k+1层的节点就是叶子节点。若m阶B树有n个关键字，那么当你找到叶子节点，其实也就等于查找不成功的节点为n+1，因此
n+1>=2x(⌈m/2⌉)^(k-1),即

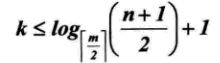
在含有n个关键字的B树上查找时，从根节点到关键字节点的路径上涉及的节点数不超多

四、B+树

　　下图B树，我们要遍历它，假设每个节点都属于硬盘的不同页面，我们为了中序遍历所有的元素，页面2-页面1-页面3-页面1-页面4-页面1-页面5.而且我们每经过节点遍历时，都会对节点中的元素进行一次遍历，糟糕！有没有可能让遍历时每个元素只访问一次呢？
　　
　　B+树是应文件系统所需而出的一种B树的变形树，在B树中，每一个元素树中只出现一次，而B+树中，出现在分支节点中的元素会被当做他们在该分支节点位置的中序后继者（叶子节点）中再次列出。另外，每一个叶子节点都会保存一个指向后一叶子节点的指针。
　　下图就是B+树，灰色关键字，在根节点出现，在叶子节点中再次列出。
　　
　　

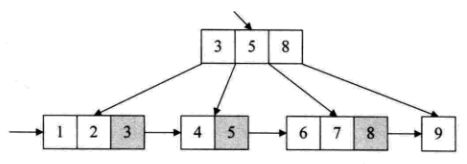
　　B+树适合随机查找，只不过查到后是索引，不能提供实际记录的访问，还需要到达包含此关键字的终端节点。非叶结点仅具有索引作用，跟记录有关的信息均存放在叶结点中。B+树适合带有范围的查找。B+树插入、删除类似B树。

五、引用参考

• 从B树、B+树、B*树谈到R 树 July经典
• B-树、B+树、B*树的区别

• B-树（B树）学习笔记

---

附加源码

#include "stdio.h"    
#include "stdlib.h"   
#include "io.h"  
#include "math.h"  
#include "time.h"

#define OK 1
#define ERROR 0
#define TRUE 1
#define FALSE 0

#define MAXSIZE 100 /* 存储空间初始分配量 */

#define m 3 /*  B树的阶，暂设为3 */ 
#define N 17 /*  数据元素个数 */ 
#define MAX 5 /*  字符串最大长度+1  */

typedef int Status; /* Status是函数的类型,其值是函数结果状态代码，如OK等 */ 

typedef struct BTNode
{
    int keynum; /*  结点中关键字个数，即结点的大小 */ 
    struct BTNode *parent; /*  指向双亲结点 */ 
    struct Node /*  结点向量类型 */ 
    {
         int key; /*  关键字向量 */ 
         struct BTNode *ptr; /*  子树指针向量 */ 
         int recptr; /*  记录指针向量 */ 
    }node[m+1]; /*  key,recptr的0号单元未用 */ 
}BTNode,*BTree; /*  B树结点和B树的类型 */ 

typedef struct
{
    BTNode *pt; /*  指向找到的结点 */ 
    int i; /*  1..m，在结点中的关键字序号 */ 
    int tag; /*  1:查找成功，O:查找失败 */ 
}Result; /*  B树的查找结果类型 */ 

/*  在p->node[1..keynum].key中查找i,使得p->node[i].key≤K＜p->node[i+1].key */ 
int Search(BTree p, int K)
{ 
    int i=0,j;
    for(j=1;j<=p->keynum;j++)
     if(p->node[j].key<=K)
       i=j;
    return i;
}

/*  在m阶B树T上查找关键字K，返回结果(pt,i,tag)。若查找成功，则特征值 */ 
/*  tag=1，指针pt所指结点中第i个关键字等于K；否则特征值tag=0，等于K的  */
/*  关键字应插入在指针Pt所指结点中第i和第i+1个关键字之间。 */
Result SearchBTree(BTree T, int K)
{ 
    BTree p=T,q=NULL; /*  初始化，p指向待查结点，q指向p的双亲  */
    Status found=FALSE;
    int i=0;
    Result r;
    while(p&&!found)
    {
     i=Search(p,K); /*  p->node[i].key≤Knode[i+1].key  */
     if(i>0&&p->node[i].key==K) /*  找到待查关键字 */ 
       found=TRUE;
     else
     {
       q=p;
       p=p->node[i].ptr;
     }
    }
    r.i=i;
    if(found) /*  查找成功  */
    {
     r.pt=p;
     r.tag=1;
    }
    else /*   查找不成功，返回K的插入位置信息 */ 
    {
     r.pt=q;
     r.tag=0;
    }
    return r;
}

/* 将r->key、r和ap分别插入到q->key[i+1]、q->recptr[i+1]和q->ptr[i+1]中 */ 
void Insert(BTree *q,int i,int key,BTree ap)
{ 
    int j;
    for(j=(*q)->keynum;j>i;j--) /*  空出(*q)->node[i+1]  */
        (*q)->node[j+1]=(*q)->node[j];
    (*q)->node[i+1].key=key;
    (*q)->node[i+1].ptr=ap;
    (*q)->node[i+1].recptr=key;
    (*q)->keynum++;
}

/* 将结点q分裂成两个结点，前一半保留，后一半移入新生结点ap */ 
void split(BTree *q,BTree *ap)
{ 
    int i,s=(m+1)/2;
    *ap=(BTree)malloc(sizeof(BTNode)); /*  生成新结点ap */ 
    (*ap)->node[0].ptr=(*q)->node[s].ptr; /*  后一半移入ap */ 
    for(i=s+1;i<=m;i++)
    {
         (*ap)->node[i-s]=(*q)->node[i];
         if((*ap)->node[i-s].ptr)
            (*ap)->node[i-s].ptr->parent=*ap;
    }
    (*ap)->keynum=m-s;
    (*ap)->parent=(*q)->parent;
    (*q)->keynum=s-1; /*  q的前一半保留，修改keynum */ 
}

/* 生成含信息(T,r,ap)的新的根结点&T，原T和ap为子树指针 */ 
void NewRoot(BTree *T,int key,BTree ap)
{ 
    BTree p;
    p=(BTree)malloc(sizeof(BTNode));
    p->node[0].ptr=*T;
    *T=p;
    if((*T)->node[0].ptr)
        (*T)->node[0].ptr->parent=*T;
    (*T)->parent=NULL;
    (*T)->keynum=1;
    (*T)->node[1].key=key;
    (*T)->node[1].recptr=key;
    (*T)->node[1].ptr=ap;
    if((*T)->node[1].ptr)
        (*T)->node[1].ptr->parent=*T;
}

/*  在m阶B树T上结点*q的key[i]与key[i+1]之间插入关键字K的指针r。若引起 */ 
/*  结点过大,则沿双亲链进行必要的结点分裂调整,使T仍是m阶B树。 */
void InsertBTree(BTree *T,int key,BTree q,int i)
{ 
    BTree ap=NULL;
    Status finished=FALSE;
    int s;
    int rx;
    rx=key;
    while(q&&!finished)
    {
        Insert(&q,i,rx,ap); /*  将r->key、r和ap分别插入到q->key[i+1]、q->recptr[i+1]和q->ptr[i+1]中  */
        if(q->keynum/*  插入完成 */ 
        else
        { /*  分裂结点*q */ 
            s=(m+1)/2;
            rx=q->node[s].recptr;
            split(&q,&ap); /*  将q->key[s+1..m],q->ptr[s..m]和q->recptr[s+1..m]移入新结点*ap  */
            q=q->parent;
            if(q)
                i=Search(q,key); /*  在双亲结点*q中查找rx->key的插入位置  */
        }
    }
    if(!finished) /*  T是空树(参数q初值为NULL)或根结点已分裂为结点*q和*ap */ 
        NewRoot(T,rx,ap); /*  生成含信息(T,rx,ap)的新的根结点*T，原T和ap为子树指针 */ 
}


void print(BTNode c,int i) /*  TraverseDSTable()调用的函数  */
{
    printf("(%d)",c.node[i].key);
}

int main()
{
    int r[N]={22,16,41,58,8,11,12,16,17,22,23,31,41,52,58,59,61};
    BTree T=NULL;
    Result s;
    int i;
    for(i=0;iif(!s.tag)
            InsertBTree(&T,r[i],s.pt,s.i);
    }
    printf("\n请输入待查找记录的关键字: ");
    scanf("%d",&i);
    s=SearchBTree(T,i);
    if(s.tag)
        print(*(s.pt),s.i);
    else
        printf("没找到");
    printf("\n");

    return 0;
}