天空盒(SkyBox)的实现原理与细节

天空盒的原理

在实时渲染中，如果要绘制非常远的物体，例如远处的山、天空等，随着观察者的距离的移动，这个物体的大小是几乎没有什么变化的，想象一下远处有一座山，即使人走进十米、百米、甚至千米，这座山的大小也是几乎不怎么改变的，这个时候可以考虑采用天空盒技术。

所谓的天空盒其实就是将一个立方体展开，然后在六个面上贴上相应的贴图，如上图所示。
在实际的渲染中，将这个立方体始终罩在摄像机的周围，让摄像机始终处于这个立方体的中心位置，然后根据视线与立方体的交点的坐标，来确定究竟要在哪一个面上进行纹理采样。具体的映射方法为：设视线与立方体的交点为 (x,y,z) ( x , y , z ) ,在 x、y、z x 、 y 、 z 中取绝对值最大的那个分量，根据它的符号来判定在哪个面上采样。

然后让其他两个分量都除以最大分量的绝对值，这样就让另外两个分量都映射到了 [0,1] [ 0 , 1 ] 内，然后就可以直接在对应的纹理上做纹理映射就行了，这个方法就是所谓的Cube Map，是天空盒方法的核心。以下是它的Vertex Shader和Pixel Shader，在Direct3D中可以直接用TextureCube，这样就省去了做Cube Map的步骤。

cbuffer MatrixType
{
    matrix WorldMatrix;
    matrix ViewMatrix;
    matrix ProjectionMatrix;
};

struct VertexInputType
{
    float4 position : POSITION;
    float2 tex : TEXCOORD0; 
};

struct PixelInputType
{
    float4 position : SV_POSITION;
    float3 tex : TEXCOORD0;
};

PixelInputType main(VertexInputType input)
{
    PixelInputType output;
    input.position.w = 1.0f;

    output.position = mul(input.position,WorldMatrix);
    output.position = mul(output.position,ViewMatrix);
    output.position = mul(output.position,ProjectionMatrix);
    output.position.z = output.position.w;

    output.tex.x = input.position.x;
    output.tex.y = input.position.y;
    output.tex.z = input.position.z;

    return output;
};

TextureCube shaderTexture;
SamplerState SampleType;

struct PixelInputType
{
    float4 position : SV_POSITION;
    float3 tex : TEXCOORD0;
};

float4 PixelFunc(PixelInputType input) : SV_TARGET
{
    return shaderTexture.Sample(SampleType,input.tex);
};

天空盒的原理非常简单，下面来探讨关于天空盒的几个细节问题。

z = w

在投影变换之后，会做一步透视除法，即让四元向量的所有分量都除以它的W分量，从而使视锥体内的区域的x、y映射到 [−1,1] [ − 1 , 1 ] ，z映射到 [0,1] [ 0 , 1 ] ，从而根据透视除法之后的 x、y、z x 、 y 、 z 的范围直接剔除掉那些不可见的顶点，如果令 z=w z = w ，就表示透视除法后的 z=1 z = 1 ，也就是让天空盒始终处于远平面的位置，从而让它被之后所有要绘制的物体遮挡住。由于 z=1 z = 1 ，要修改深度测试的比较函数，即令 CD3D11_DEPTH_STENCIL_DESC 的desc.DepthFunc = D3D11_COMPARISON_LESS_EQUAL，如果比较函数是小于的话，由于深度缓冲的最大值本来就是1，无法通过深度测试的比较函数，最终天空盒是没办法被绘制出来的。

消隐问题

由于摄像机位于物体的内部，这个时候消隐的设置尤为重要，模型本身是没有发生变化的，它的法线始终朝向外部，那么视线与法线的夹角就变成了锐角，如果采用背面消隐，整个模型就会都被剔除掉，所以在绘制天空盒的时候，要么取消消隐，要么将消隐设置为正面消隐。

天空盒模型大小的限制

原则上模型的大小对于最终的结果没有影响，因为在模型增大的时候，虽然它的面是变大了，但它离视锥也变远了，因此最终视野内的大小是保持不变的，但是一定要保证模型始终处在视锥体的内部，即让模型离摄像机最远的点到摄像机的距离不超过摄像机到远平面的距离，对于一个立方体模型来说，离中心最远的点显然是它的顶点，

d=3–√2a d = 3 2 a

a a 为立方体的边长，由

d≤Zfar d ≤ Z f a r

得

a≤23–√Zfar a ≤ 2 3 Z f a r

因此天空盒的模型边长有一个上界，在这个最大值以内都是可以的。

天空盒纹理的最佳大小

最终渲染的效果很大程度上取决于纹理大小与屏幕大小之间的关系，如果要达到最佳的效果，肯定是要让纹理中的每一个纹素对应窗口中的每一个像素，此时纹理大小与窗口大小的关系为：

Tsize=Rwidthtan(fov/2) T s i z e = R w i d t h t a n ( f o v / 2 )

其中 Tsize T s i z e 为纹理的大小， Rwidth R w i d t h 为窗口的宽度， fov f o v 为视锥体的视角。
下面来进行推导：

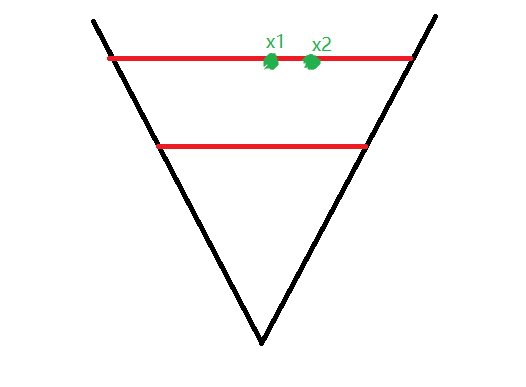
取远平面上的两点，设它们的x坐标分别为 x1 x 1 、 x2 x 2 ，这两点显然就是天空盒上的两点。
现在计算它们归一化后在窗口屏幕上的坐标：

rx1=(x1d∗tan(fov/2)+1.0)2∗rwidth r x 1 = ( x 1 d ∗ t a n ( f o v / 2 ) + 1.0 ) 2 ∗ r w i d t h

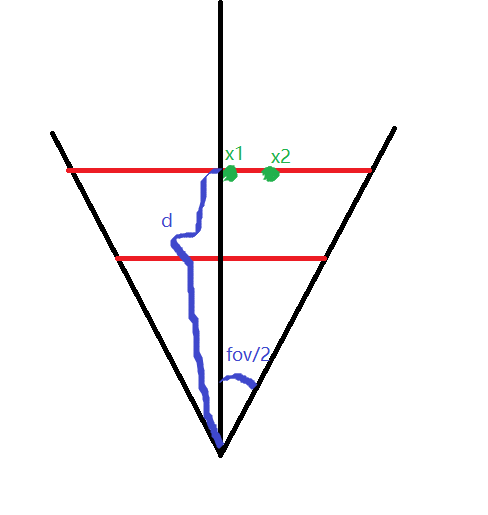
解释一下：其中 x1d∗tan(fov/2) x 1 d ∗ t a n ( f o v / 2 ) 将 x1 x 1 映射到 [−1,1] [ − 1 , 1 ] ，再加1并除以2就映射到了 [0,1] [ 0 , 1 ]
同理

rx2=(x2d∗tan(fov/2)+1.0)2∗rwidth r x 2 = ( x 2 d ∗ t a n ( f o v / 2 ) + 1.0 ) 2 ∗ r w i d t h

现在，假设x1、x2映射到屏幕上后两者的x坐标差1，即相隔1个像素：

rx2−rx1=1 r x 2 − r x 1 = 1

代入上面两式可得：

(x2d∗tan(fov/2))−(x1d∗tan(fov/2))2∗rwidth=1 ( x 2 d ∗ t a n ( f o v / 2 ) ) − ( x 1 d ∗ t a n ( f o v / 2 ) ) 2 ∗ r w i d t h = 1

即

x2−x1=2∗d∗tan(fov/2)rwidth(1) (1) x 2 − x 1 = 2 ∗ d ∗ t a n ( f o v / 2 ) r w i d t h

由之前所述，最佳情况是屏幕上的一个像素对应纹理中的一个纹素，那么就意味着x1、x2映射到纹理中也应该差1。
由CubeMap的方法：

Tx1=x1d+12∗Tsize T x 1 = x 1 d + 1 2 ∗ T s i z e

Tx2=x2d+12∗Tsize T x 2 = x 2 d + 1 2 ∗ T s i z e

由

Tx2−Tx1=1 T x 2 − T x 1 = 1

得：

x2−x1=2∗dTsize x 2 − x 1 = 2 ∗ d T s i z e

将其带入(1)式即可得

Tsize=Rwidthtan(fov/2) T s i z e = R w i d t h t a n ( f o v / 2 )

有的时候可能纹理的大小被局限在256*256以内，那么对于一些较大的窗口来说，最终纹理会被拉伸，影响最终的渲染结果。如果对质量要求不高，很多情况下这样拉伸的结果也是可以接受的，但如果对质量有一定的要求的话，可以对天空盒做一个分块处理，保留原来的CubeMap方式不变，在做纹理映射的时候，将其分成几个小块来处理，每个小块分别是合适大小的纹理，如图所示：