计算机图形学：颜色模型、图像基本知识、Phong光照模型

颜色模型、图像基本知识、Phong光照模型

1.颜色模型

1.1 RGB Color Space

The reason why we pick red, green, and blue?

• essentially because of the structure of our visual system
• Our visual system is sensitive to those three colors

缺陷

Unfortunately ,Some colors cannot be written as combinations of RGB triples, because some parts of the red curve is negative

1.2 CMY

Cyan(青), magenta（品红） , and yellow

It’s called subtractive primaries（减色系统）

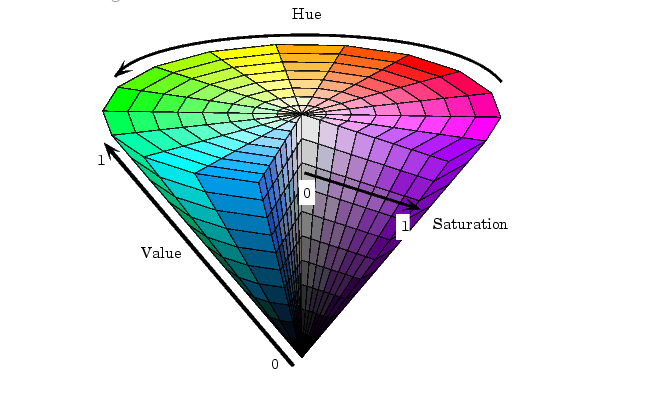
1.3 HSV Color space

RGB 不是很直观，HSV比较易于理解

• Hue (色调) means the base color, which is a main factor indicates difference between colors.
• Saturation(饱和度) is for purity of color (decrease = adding white)
• Value of brightness(亮度) Luminance of lights,(decrease = adding black)

2.图像基本知识

2.1 Image & Pixel

• Image could be treated as a 2-dimensional
  discrete function f(x,y)
• each discrete grid is called pixel

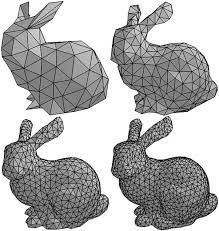
2.2 Triangle Mesh

Contains a list of faces F, and a list of vertices V

• A list of faces F = (f1,f2,…,fn), Each face is a triangle
• A list of vertices V = (v1,v2,…,vn), Each face in F is a list of indices in V

e.g.

f1–(v1,v2,v3 ), f2 --(v4,v5,v6 ),
f3–(v7,v8,v9 ), …

2.3 Normal

2.3.1 Face Normal

Each face has a normal direction to define the orientation

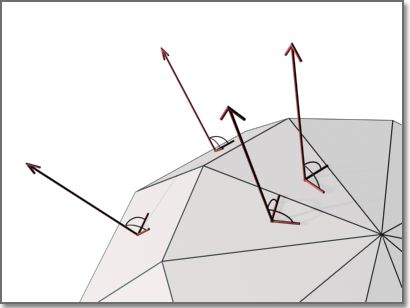
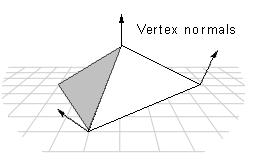
2.3.2 Vertex Normal

Each vertex is shared by m faces

计算方法

• 直接平均：Compute normal by Interpolation Nv= (Nf1+Nf2 … + Nfm)/m
• 面积加权平均：or by area based Interpolation Nv= (|F1|*Nf1+|F2|*Nf2 … + |Fm|*Nfm)/(|F1|+|F2|+…|Fm|)
• 角度加权平均：or by angle based Interpolation Nv= (|A1|*Nf1+|A2|*Nf2 … + |Am|*Nfm)/(|A1|+|A2|+…|Am|)

3.光照模型

Local Lighting

• Concerned with how objects are directly illuminated by light sources

Global Lighting

• Includes shadow effects
• Includes lighting effects from locations other than light sources, such as reflections, refractions

3.1 History of Lighting

• In 1967, Wylie: first added lighting effects into rendering
  • Intensity is inverse of the distance to the light
• In 1970, Bouknight: introduced the first lighting
  model:
  • Lambert diffuse reflection(漫发射) + ambient (No specular lighting)（环境光）
• In 1971, Gourand: gourand shading
  • Lambert diffuse + Bicentric interpolation
• In 1975, Phong: proposed extended the model by further considering specular:
  • Diffuse（漫发射） + ambient（环境光,模拟全局光照效果） + specular（高光）
  • The most influenced lighting model

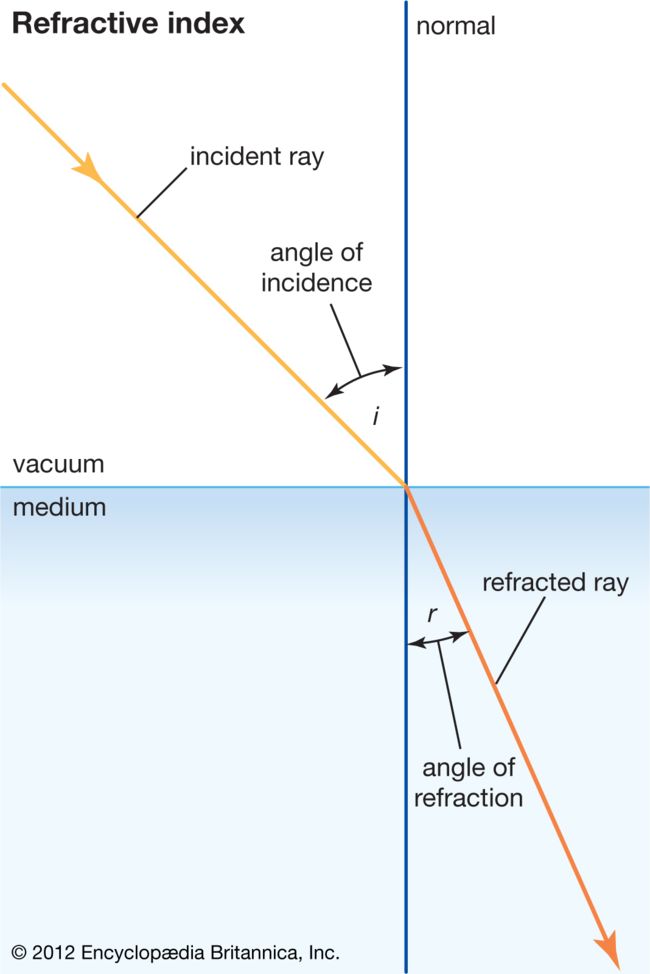
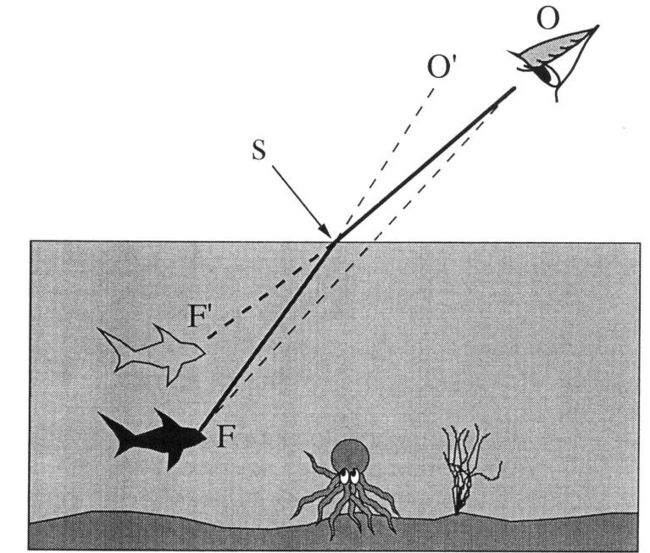
3.2折射向量的计算

• $incidence\_ray$: 入射角（单位向量）

• $normal\_vec$ = Vector(0, 0, 1) //法向量

• $refractive\_index$: 介质密度比（空气/水）

$$\begin{gathered} \cos {\theta }_i=-incidence\_ray.dot(normal\_vec) \\ \cos {\theta }_r=\sqrt{1-refractive\_inde{x}^2\ast (1-{\cos {\theta }_i}^2)}(大于0时) \\ refracted\_ray=(normal\_vec\ast \cos {\theta }_i+incidence\_ray)\ast refractive\_index-normal\_vec\ast \cos {\theta }_r \end{gathered}$$

3.3 Measure of light

• Solid Angle（立体角） :
  • How big an object appears to an observer at point P
  • Max Vaule: 4π

$$dw=\frac{ds}{r^2}$$

• Irradiance （辉度） E
  • E defined as: light energy per unit time arrived at per unit area (ds)
• Radiance （发光强度） I
  • I defined as: irradiance per unit solid angle

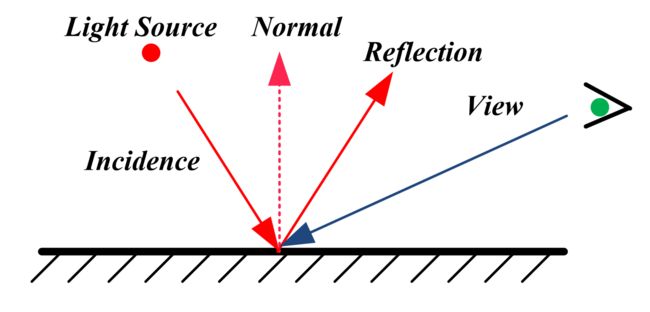
3.4 Phong Lighting Model

3.4.1 Diffuse reflection

• 漫反射光的传播是各向同性的（isotropic）
• The intensity of diffuse reflection is defined as:

$$I_d=I_i{K}_d\ast (L\cdot N)$$

• $k_d$is the diffuse reflection constant $(k_{dr},k_{dg},K_{db})$
• $k_d$implies the base color of the model

3.4.2 Specular reflection

• The intensity of specular reflection is defined as:

$$I_s=I_i{K}_s\ast (R\cdot V{)}^n$$

• $k_s$is the specular reflection constant ;
• and n is the shininess constant, which decides how shiny the surface is. n越大，高光越集中

3.4.3 Ambient reflection

• To approximate global illuminations (including indirect lighting, indirect reflection…)
• The intensity of ambient reflection is defined as:

$$I_a=I_i{K}_a$$

• $K_a$is the ambient reflection constant

3.4.4 最终结果

The reflection intensity is the sum of diffuse reflection, specular reflection and ambient reflection:

$$I=I_i{K}_a+I_i{K}_s\ast (R\cdot V{)}^n+I_i{K}_d\ast (L\cdot N)$$

3.5 Blinn-Phong Lighting Model

$$\begin{gathered} H=\frac{L+V}{2} \\ {I}_s=I_i{K}_s\ast (N\cdot H{)}^n \end{gathered}$$