最短路问题
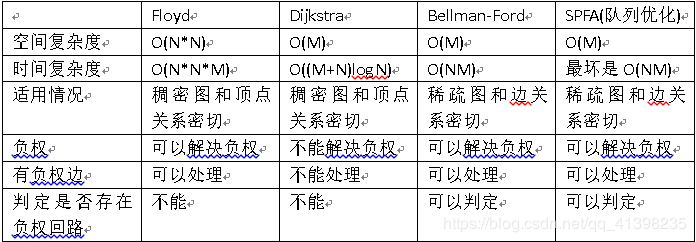
最短路问题 常用的解决方法
这里只是自己的一点小理解,只是用于以后用到的时候不至于很生疏,还请路过的大牛们轻喷
先附上最短路问题和最小生成树问题的区别:
最小生成树能够保证整个拓扑图的所有路径之和最小,但不能保证任意两点之间是最短路径。
最短路径是从一点出发,到达目的地的路径最小。
1.最简单暴力的算法 Floyd-Warshall
核心代码:
for(int k=1;k<=n;k++)
for(int i=1;i<=n;i++)
for(int j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j]
基本思想:
最开始只允许经过1号顶点进行中转,接下来只允许经过1和2号顶点进行中转…允许经过1-n号顶点进行中转,求
任意两点之间的最短路程。用一句话概括:从i号顶点到j号顶点只经过前k号店的最短路程。其实这是一种“动态规
划”的思想。该方法时间复杂度过高,可以处理带有负权边的问题但是不可以处理带有负权回路的问题
#include
using namespace std;
int main(){
int e[10][10],k,i,j,n,m,t1,t2,t3;
int inf=99999999;
cin>>n>>m;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=inf;
for(i=1;i<=m;i++){
cin>>t1>>t2>>t3;
e[t1][t2]=t3;
}
for(k=1;k<=n;k++)
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(e[i][j]>e[i][k]+e[k][j])
e[i][j]=e[i][k]+e[k][j];
for(i=1;i<=n;i++){
for(j=1;j<=n;j++){
cout< 这个代码就可以求出两点之间的最短路,就是最短距离
2.Dijkstra算法-单源最短路
步骤:
1.将所有的顶点分为两部分:已知最短路程的顶点集合P和未知最短路径的顶点集合Q。最开始,已知最短路径的顶
点集合P中只有源点一个顶点。这里我们用一个book数组记录哪些点在集合P中。例如对于某个顶点i,如果book[i]
为1则表示这个顶点在集合P中,如果book[i]为0则表示这个顶点在集合Q中。
2.设置源点s到自己的最短路径为0即dis[s]=0。若存在有源点能直接到达的顶点i,则把dis[i]设为e[s][i]。同时把所有
其他(源点不能直接到达的)顶点的最短路径设为∞。
3.在集合Q的所有顶点中选择一个离源点s最近的顶点u(即dis[u]最小)加入到集合P。并考察所有以点u为起点的边,
对每一条边及进行松弛。例如存在一条从u到v的边,那么可以通过将边u->v添加到尾部来拓展一条从s到v的路径,
这条路径的长度是dis[u]+e[u][v]。如果这个值比目前已知的dis[v]的值要小,我们可以用新值来代替前dis[v]中的
值。
4.重复第三步,如果集合Q为空,算法结束。最终dis数组中的值就是源点到所有顶点的最短路径。
Dij的模板代码,具体的问题还需要具体的分析
#include
using namespace std;
int main(){
int e[10][10],dis[10],book[10],i,j,n,m,t1,t2,t3,u,v,min;
int inf=99999999;
cin>>n>>m;
for(i=1;i<=n;i++)
for(j=1;j<=n;j++)
if(i==j)
e[i][j]=0;
else
e[i][j]=inf;
for(i=1;i<=m;i++){
cin>>t1>>t2>>t3;
e[t1][t2]=t3;
}
for(i=1;i<=n;i++)
dis[i]=e[1][i];
for(i=1;i<=n;i++)
book[i]=0;
book[1]=1;
//Dijkstra算法核心语句
for(i=1;i<=n-1;i++){
min=inf;
for(j=1;j<=n;j++){
if(book[j]=0&&dis[j]dis[u]+e[u][v])
dis[v]=dis[u]+e[u][v];
}
}
}
for(i=1;i<=n;i++)
cout< 补充
接下来补充一下用邻接表存储来表示这个图的方法,这里用的是“数组”来间接实现邻接表,当然也可以直接使用邻
接表进行操作,只是用“数组”表示的方法更加方便
int n,m;
int u[6],v[6],w[6];
int first[5],next[5];
cin>>n>>m;
for(int i=1;i<=n;i++)
first[i]=-1;
for(int i=1;i<=m;i++){
cin>>u[i]>>v[i]>>w[i];
next[i]=first[u[i]];
first[u[i]]=i;
}
这里就是实现邻接表的过程,当然数组的大小要根据实际情况而确定
3. Bellman-Ford----解决负权边
核心代码
for(k=1;k<=n-1;k++)
for(i=1;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
该算法可以解决带有负权边的图的问题
上面的代码中,外循环一共循环了n-1次(n为顶点的个数),内循环循环了m次(m为边的个数),即枚举每一条
边。dis数组的作用与Dijkstra算法一样,是用来记录源点到其余各个顶点的最短路径。u,v和w三个数组是用来记录
边的信息。例如第i条边存储在u[i],v[i]和w[i]中,表示从顶点u[i]到顶点v[i]这条边(u[i]->v[i])权值为w[i]
if(dis[v[i]]>dis[u[i]]+w[i])
dis[v[i]]=dis[u[i]]+w[i];
上面这两行代码是看看能否通过u[i]->vi这条边,使得1号顶点到v[i]号顶点的距离变短。即1号顶点到
u[i]号顶点的距离(dis[u[i]])加上u[i]->v[i]这条边(权值为w[i])的值是否会比原先1号顶点到v[i]号顶点的距离(dis[v[i]])要
小。这一点其实与Dijkstra的“松弛”操作是一样的。
注意
另外,第一轮在对所有的边进行松弛之后,得到的是从1号顶点“只能经过一条边”到达其余各个顶点的最短路径长
度。在第2轮在对所有的边进行松弛之后,得到的是从1号顶点“最多经过两条边”到达其余各个顶点的最短路径长
度。如果进行k轮的话,得到的就是1号顶点“最多经过k条边”到达其余各个顶点的最短路径长度。一共需要进行n-1
轮就可以了。因为在一个含有n个顶点的图中,任意两点之间的最短路径最多包好n-1边。
#include
using namespace std;
int main(){
int dis[10],bak[10],i,k,n,m,u[10],v[10],w[10],check,flag;
int inf=99999999;
cin>>n>>m;
for(i=1;i<=m;i++)
cin>>u[i]>>v[i]>>w[i];
for(i=1;i<=n;i++)
dis[i]=inf;
dis[1]=0;
for(k=1;k<=n-1;k++){
check=0; //用来标记在本轮松弛中数组dis是否发生更新
//进行一轮松弛
for(i=1;i<=m;i++){
if(dis[v[i]]>dis[u[i]]+w[i]){
dis[v[i]]=dis[u[i]]+w[i];
check=1;
}
}
if(!check)
break;
}
//检测负权回路
flag=0;
for(i=1;i<=m;i++)
if(dis[v[i]]>dis[u[i]]+w[i])
flag=1;
if(flag)
cout<<"此图含有负权回路";
else{
//输出最终的结果
for(i=1;i<=n;i++)
cout< 4. Bellman-Ford的队列优化(SPFA)
每次选取队首顶点u,对顶点u的所有出边进行松弛操作。例如有一条u->v的边,如果通过u->v这条边是的源点到顶点v的最短路程变短(dis[u]+e[u][v] 每次从队首(head)取出一个顶点,并对与其相邻的所有顶点进行松弛操作,若某个相邻的顶点松弛成功,且这个相 邻的顶点不在队列中(不在head和tail之间),则将它加入到队列中。对当前顶点处理完毕后立即出队,并对下一 个新队首进行如上操作,直到队列为空时算法结束。这里用了一个数组book来记录每个顶点是否在队列中。#include