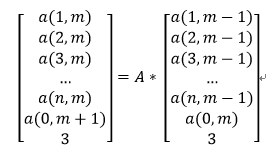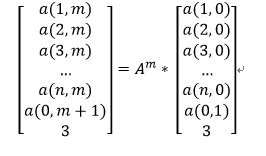hdu5015 233 Matrix 矩阵快速幂 矩阵构造方法
233 Matrix
题目的意思是有一个叫做233 Matrix的矩阵。
给定第一行元素a(0, 1) = 233, a(0, 2) = 2333, a(0, 3) = 23333, ..., a(0, n) = 10 * a(0, n - 1) + 3, (n >= 2)。
第一列元素a(1, 0), a(2, 0), a(3, 0), ..., a(n, 0),和一个递推式子a(i ,j) = a(i - 1, j) + a(i, j - 1), (
i,j ≠ 0),让你求出a(n, m) mod
10000007的值。
其中,a(0, 0)应该等于0,n和m及第一列元素由输入给定。数据范围为n ≤ 10,m ≤ 109
因为数据量很大,暴力求解肯定是不行的。必定超时,虽然给定的时间是5秒钟。
那接下来就是推公式了,而我最终也真的推出来个公式,但很遗憾,它只有当n和m相等的时候才成立,可是n最大才为10,这种思路也就被否定了。
既然给定的是一个矩阵的形式,难道可以用矩阵快速幂搞出来?可以试试。注意一点,如果能构造出来快速幂的话,也只有按列来推。
对于给定的递推式a(i ,j) = a(i - 1, j) + a(i, j - 1),将它展开则a(i, j) = a(i - 1, j) + a(i, j - 1) = a(i - 2, j) + a(i - 1, j - 1) + a(i, j - 1) = a(i - 3, j) + a(i - 2, j - 1) + a(i - 1, j - 1) + a(i, j - 1) = ...
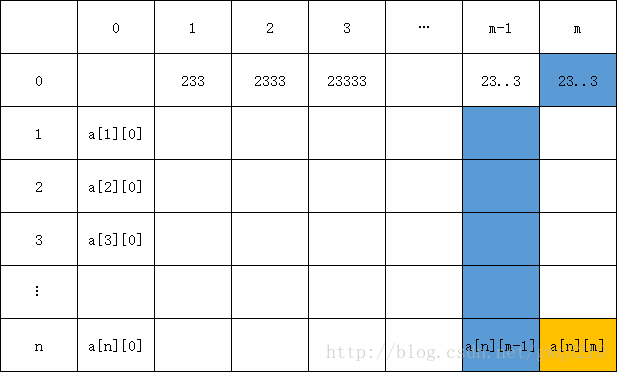
很快就可以发现规律了得到:a(i, j) = a(1, j - 1) + a(2, j - 1) + ... + a(i, j - 1) + a(0, j)。
如下图:
图片橙色部分等于蓝色部分的和,也就是上边的公式。
我们的目的是由当前蓝色的部分,推出与它紧邻的右边下一列蓝色的部分。
构造如下矩阵,我们希望找出一个n+1阶的方阵,使得如下矩阵式成立。
根据上述推导的公式,可得A矩阵的第一行为[1 0 ... 0 1],
第二行为[1 1 0 ... 0 1],第三行为[1 1 1 0 ... 0 1],。。。,第n行为[1 1 1 ... 1 1]。
遗憾的是第n+1行无论怎么取值也无法是矩阵式成立。
因为a(0, m + 1) = a(0,m)* 10 + 3,那么显然n+1行的矩阵不能满足要求,可以将矩阵变成n+2行最后一行为3。则矩阵就变成:
相应的A矩阵第一行为
[1 0 ... 0 1 0],
第二行为[1 1 0 ... 0 1 0],第三行为[1 1 1 0 ... 0 1 0],。。。,第n行为[1 1 1 ... 1 1 0],
第n+1行为[0 0 0 0 .... 0 10 1],
第n+2行为[0 0 0 0 ... 0 0 1]。则矩阵A的形式如下:
由于矩阵乘法的结合律,可得:
这样就可以对矩阵A^m使用矩阵快速幂了。
代码如下(代码中构造的矩阵可能和上述矩阵不符):
/*************************************************************************
> File Name: matrix.cpp
> Author: gwq
> Mail: [email protected]
> Created Time: 2014年09月18日 星期四 08时32分40秒
************************************************************************/
#include
#include
#include
#include
#include
#include
#include
#include