Leetcode题解-算法-数组与矩阵
文章目录
- 1、把数组中的0移动到数组尾部
- 2、改变矩阵分维度
- 3、数组中连续1的最大个数
- 4、有序矩阵中查找目标数
- 5、有序矩阵中第k小的数
- 6、1-n的数中一个数被另一个替换,找重复和丢失的数
- 7、寻找数组中丢失的数
- 8、寻找数组中重复的数
- 9、寻找数组中重复的数(不修改数组)
- 10、构造相邻数有 k 种差值的数组
- 11、数组的度
- 12、对角元素相等的矩阵
- 13、数组嵌套
- 14、分隔数组
1、把数组中的0移动到数组尾部
283. Move Zeroes(Easy)
Given an array nums, write a function to move all 0’s to the end of it while maintaining the relative order of the non-zero elements.
Example:
Input: [0,1,0,3,12]
Output: [1,3,12,0,0]
Note:
You must do this in-place without making a copy of the array.
Minimize the total number of operations.
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int len=nums.size();
int k=0;
for(int i=0;i<len;i++)
{
if(nums[i]!=0)
nums[k++]=nums[i];
}
for(;k<len;k++)
nums[k]=0;
}
};
2、改变矩阵分维度
566. Reshape the Matrix(Easy)
In MATLAB, there is a very useful function called ‘reshape’, which can reshape a matrix into a new one with different size but keep its original data.
You’re given a matrix represented by a two-dimensional array, and two positive integers r and c representing the row number and column number of the wanted reshaped matrix, respectively.
The reshaped matrix need to be filled with all the elements of the original matrix in the same row-traversing order as they were.
If the ‘reshape’ operation with given parameters is possible and legal, output the new reshaped matrix; Otherwise, output the original matrix.
Example 1:
Input:
nums =
[[1,2],
[3,4]]
r = 1, c = 4
Output:
[[1,2,3,4]]
Explanation:
The row-traversing of nums is [1,2,3,4]. The new reshaped matrix is a 1 * 4 matrix, fill it row by row by using the previous list.
Example 2:
Input:
nums =
[[1,2],
[3,4]]
r = 2, c = 4
Output:
[[1,2],
[3,4]]
Explanation:
There is no way to reshape a 2 * 2 matrix to a 2 * 4 matrix. So output the original matrix.
Note:
- The height and width of the given matrix is in range [1, 100].
- The given r and c are all positive.
class Solution {
public:
vector<vector<int>> matrixReshape(vector<vector<int>>& nums, int r, int c) {
int row=nums.size();
int col=nums[0].size();
if(row*col!=r*c)
return nums;
int t=0;
vector<vector<int>>result(r,vector<int>(c,0));//初始化一个二维数组
for(int i=0;i<r;i++)
{
for(int j=0;j<c;j++)
{
result[i][j]=nums[t/col][t%col];
t++;
}
}
return result;
}
};
3、数组中连续1的最大个数
485. Max Consecutive Ones(Easy)
Given a binary array, find the maximum number of consecutive 1s in this array.
Example 1:
Input: [1,1,0,1,1,1]
Output: 3
Explanation: The first two digits or the last three digits are consecutive 1s.The maximum number of consecutive 1s is 3.
Note:
- The input array will only contain 0 and 1.
- The length of input array is a positive integer and will not exceed 10,000
class Solution {
public:
int findMaxConsecutiveOnes(vector<int>& nums) {
int ma=0,cur=0;
for(int c:nums)
{
cur=(c==0?0:cur+1);
ma=max(ma,cur);
}
return ma;
}
};
4、有序矩阵中查找目标数
240. Search a 2D Matrix II(Medium)
Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:
- Integers in each row are sorted in ascending from left to right.
- Integers in each column are sorted in ascending from top to bottom.
Example:
Consider the following matrix:
[
[1, 4, 7, 11, 15],
[2, 5, 8, 12, 19],
[3, 6, 9, 16, 22],
[10, 13, 14, 17, 24],
[18, 21, 23, 26, 30]
]
Given target = 5, return true.
Given target = 20, return false.
问题分析:
矩阵具有特殊性:每行从左到右的升序排列;每列从上到下升序排列。
从矩阵的右上角开始搜索,若目标值小于矩阵元素,向左运动,若目标值大于矩阵元素,向下运动。
class Solution {
public:
bool searchMatrix(vector<vector<int>>& matrix, int target) {
int row=matrix.size();
if(row==0)
return false;
int col=matrix[0].size();
int r=0,c=col-1;
while( r<row && c>=0)
{
if(matrix[r][c]==target)
return true;
if(target>matrix[r][c])
r++;
else
c--;
}
return false;
}
};
5、有序矩阵中第k小的数
378. Kth Smallest Element in a Sorted Matrix(Medium)
Given a n x n matrix where each of the rows and columns are sorted in ascending order, find the kth smallest element in the matrix.
Note that it is the kth smallest element in the sorted order, not the kth distinct element.
Example:
matrix = [
[ 1, 5, 9],
[10, 11, 13],
[12, 13, 15]
],
k = 8,
return 13.
Note:
You may assume k is always valid, 1 ≤ k ≤ n2.
方法一:二分法
区间头尾分别为矩阵最小值和最大值,每次区间统计矩阵中小于等于 mid 的数有多少个。循环求解是为了找到使得矩阵中元素 matrix[i][j]<=mid 的 mid 的最小值,也就是第 k 小的数。
循环条件为 while(high>=low),因为如果刚好 mid 是我们要的值时,由于统计结果 cnt==k,导致 high=mid-1;需要再循环一次将low++;
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
int row=matrix.size();
int col=matrix[0].size();
int low=matrix[0][0];
int high=matrix[row-1][col-1];
while(high>=low)
{
int mid=low+(high-low)/2;
int cnt=0;
for(int i=0;i<row;i++)
{
for(int j=0;j<col&&matrix[i][j]<=mid;j++)
cnt++;
}
if(cnt>=k)
high=mid-1;
else
low=mid+1;
}
return low;
}
};
方法二:堆
将所有元素放入堆中,默认是大顶锥,将元素弹出至堆中元素剩下 k 个,堆顶元素就是结果。
class Solution {
public:
int kthSmallest(vector<vector<int>>& matrix, int k) {
int row=matrix.size();
int col=matrix[0].size();
priority_queue<int>qu;
for(int i=0;i<row;i++)
{
for(int j=0;j<col;j++)
qu.push(matrix[i][j]);
}
int count=row*col-k;
for(int i=0;i<count;i++)
qu.pop();
return qu.top();
}
};
6、1-n的数中一个数被另一个替换,找重复和丢失的数
645. Set Mismatch(Easy)
Example 1:
Input: nums = [1,2,2,4]
Output: [2,3]
问题分析:
1、最直接的方法就是排序,找出重复的数,时间复杂度为O(nlogn)。
2、也可以统计元素出现的个数,找到重复的数。时间复杂度为O(n),空间复杂度O(n)。
3、将数组中每个元素作为下标,将该下标的元素置反,两次置反时,该数组元素为重复元素,时间复杂度为O(n),空间复杂度O(1)。
4、通过交换数组元素,使得数组上的元素在正确的位置上,时间复杂度为O(n),空间复杂度为O(1)。
方法一:排序
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
sort(nums.begin(),nums.end());
int n=nums.size();
int sum=0;
vector<int>res(2,0);
for(int i=0;i<n-1;i++)
{
if(nums[i]==nums[i+1]) //重复的数
res[0]=nums[i];
sum=sum+nums[i];
}
sum=sum+nums[n-1];
res[1]=(1+n)*n/2-(sum-res[0]); //丢失的数
return res;
}
};
方法二:统计每个元素出现的次数
将元素放入map中,再查看每个元素出现的个数。
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
map<int,int>m;
int n=nums.size();
int sum=0;
vector<int>res(2,0);
for(int i=0;i<n;i++)
{
++m[nums[i]];
sum=sum+nums[i];
}
for(auto iter = m.begin(); iter != m.end(); iter++)
if(iter->second==2)
res[0]=iter->first;
res[1]=(1+n)*n/2-(sum-res[0]);
return res;
}
};
可以用数组统计每个元素出现的次数,数组下标为对应的数值,数组中元素为每个元素出现的次数。
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
int n=nums.size();
vector<int>vec(n+1,0);//下表为数据值,元素为出现的次数
vector<int>res(2,0);
int sum=0;
for(int i=0;i<n;i++)
{
vec[nums[i]]++;
sum=sum+nums[i];
}
for(int i=1;i<=n;i++)
{
if(vec[i]>1)
{
res[0]=i;//下标就是对应的数据值
break;
}
}
res[1]=(1+n)*n/2-(sum-res[0]);
return res;
}
};
时间复杂度:O(n), 空间复杂度:O(n)。
方法三:元素置反
nums 数组中的所有元素都是1到n的正数。对于 nums 中的每个元素 n,找数组中的第 n 个元素,如果为正数,乘以-1。 如果其中一个元素 j 出现两次,当第二次遇到这个数字时,将发现元素 nums[ |i|-1] 为负数。,此时 j 就是重复的元素。
完成反转后,如果其中一个数字 j 缺失,则第 j 个元素将为正数,即找到了缺失的数字。
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
vector<int>res(2,0);
for (int n : nums)
{
if (nums[abs(n) - 1] < 0)
res[0] = abs(n);
else
nums[abs(n) - 1] *= -1;
}
for (int i = 0; i < nums.size(); i++) {
if (nums[i] > 0)
res[1] = i + 1;
}
return res;
}
};
时间复杂度:O(n), 空间复杂度:O(1)。
方法四:调整到正确位置上
通过交换,把每个元素都换到对应的位置上,最后下标为 i 的位置上如果元素不是 i+1,说该数丢失。
class Solution {
public:
vector<int> findErrorNums(vector<int>& nums) {
vector<int>res(2,0);
int n=nums.size();
for(int i=0;i<n;i++)
{
while(nums[i]!=i+1 && nums[nums[i]-1]!=nums[i])//直到换到数字i+1为止
swap(nums[i],nums[nums[i]-1]);
}
for(int i=0;i<n;i++)
{
if(nums[i]!=i+1)
{
res[0]=nums[i];
res[1]=i+1;
}
}
return res;
}
};
类似的题目还有:
448. Find All Numbers Disappeared in an Array(Easy)寻找数组中丢失的数,见第7题
442. Find All Duplicates in an Array(Medium)寻找数组中重复的数,见第8题
7、寻找数组中丢失的数
448. Find All Numbers Disappeared in an Array(Easy)
Given an array of integers where 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.Find all the elements of [1, n] inclusive that do not appear in this array.
Could you do it without extra space and in O(n) runtime? You may assume the returned list does not count as extra space.
Example:
Input:
[4,3,2,7,8,2,3,1]
Output:
[5,6]
数组中的元素为 1-n,现在其中一些数出现两次,其他的出现一次,找出1-n 中没有出现的数。
方法一:
统计每种数字出现的频率,时间复杂度:O(n), 空间复杂度:O(n)。
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n=nums.size();
vector<int>vec(n+1,0);
vector<int>res;
for(int c:nums)
vec[c]++;
for(int i=1;i<=n;i++)
if(vec[i]==0)
res.push_back(i);
return res;
}
};
方法二:
1-n 的每个元素,如果出现,就将对应位置上的元素置反,最后没有置反的位置就是没有出现的元素。时间复杂度:O(n), 空间复杂度:O(1)。
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n=nums.size();
vector<int>res;
for(int c:nums)
{
if(nums[abs(c)-1]>0)
nums[abs(c)-1]*=-1;
}
for(int i=0;i<n;i++)
if(nums[i]>0)
res.push_back(i+1);
return res;
}
};
方法三:
交换,把元素交换到正确的位置上
class Solution {
public:
vector<int> findDisappearedNumbers(vector<int>& nums) {
int n=nums.size();
vector<int>res;
for(int i=0;i<n;i++)
{
while(nums[i]!=i+1 && nums[i]!=nums[nums[i]-1])
swap(nums[i],nums[nums[i]-1]);
}
for(int i=0;i<n;i++)
if(nums[i]!=i+1)
res.push_back(i+1);
return res;
}
};
8、寻找数组中重复的数
442. Find All Duplicates in an Array(Medium)
Given an array of integers, 1 ≤ a[i] ≤ n (n = size of array), some elements appear twice and others appear once.Find all the elements that appear twice in this array.
Could you do it without extra space and in O(n) runtime?
Example:
Input:
[4,3,2,7,8,2,3,1]
Output:
[2,3]
方法一:直接统计每种元素出现的个数,时间复杂度:O(n), 空间复杂度:O(n)。
方法二:置反
数组中每个数字 c,如果第 c 个数子大于0,即 nums[abs©-1]>0,将数组中第 c 个元素置反,即为 nums[abs©-1]*=-1; 如果 nums[abs©-1]<0,说明数组 c 已经出现过了,重复了。时间复杂度:O(n), 空间复杂度:O(1)。
class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
vector<int>res;
for(int c:nums)
{
if(nums[abs(c)-1]>0)
nums[abs(c)-1]*=-1;
else
res.push_back(abs(c));
}
return res;
}
};
方法三:调整到正确位置上
class Solution {
public:
vector<int> findDuplicates(vector<int>& nums) {
int n=nums.size();
vector<int>res;
for(int i=0;i<n;i++)
{
while(nums[i]!=i+1 && nums[i]!=nums[nums[i]-1])
swap(nums[i],nums[nums[i]-1]);
}
for(int i=0;i<n;i++)
if(nums[i]!=i+1)
res.push_back(nums[i]);
return res;
}
};
9、寻找数组中重复的数(不修改数组)
287. Find the Duplicate Number(Medium)
Given an array nums containing n + 1 integers where each integer is between 1 and n (inclusive), prove that at least one duplicate number must exist. Assume that there is only one duplicate number, find the duplicate one.
Example 1:
Input: [1,3,4,2,2]
Output: 2
Example 2:
Input: [3,1,3,4,2]
Output: 3
Note:
- You must not modify the array (assume the array is read only).
- You must use only constant, O(1) extra space.
- Your runtime complexity should be less than O(n2).
- There is only one duplicate number in the array, but it could be repeated more than once.
不能修改原数组元素,空间复杂度为O(1) ,时间复杂度小于O(n2)
方法一:Floyd判圈算法
元素有重复,可以看成数组中存在环,寻找环的入口结点。用快慢指针 slow,fast,slow 一次走一步,fast 一次走两步,二者相遇时,一定在环中。相遇之后让 fast 指向数组开始位置,slow,fast 一次走一步,则在环入口相遇。
class Solution {
public:
int findDuplicate(vector<int>& nums) {
int res=0;
int slow=nums[0];
int fast=nums[nums[0]];
while(slow!=fast)
{
slow=nums[slow];
fast=nums[nums[fast]];
}
fast=0;
while(slow!=fast)
{
slow=nums[slow];
fast=nums[fast];
}
return slow;
}
};
链表找环的入口(证明)
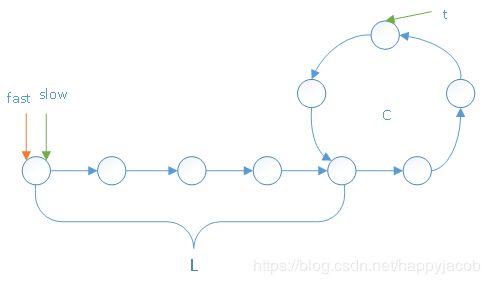
链表的非环部分长度为L,环的长度为C,相遇时slow指针走了t步。则有如下表达式。
(t-L) mod C = (2t-L) mod C
(t-L) - m*C = (2t-L) - n*C
t = (n - m)*C
只要n,m为正整数,一定有解。此时将fast放回链表头部,slow原地不动,再走t1步,slow走到环的入口,则有
(t+t1-L) mod C = 0
解得t1=L。即两指针相遇处为环的入口。
10、构造相邻数有 k 种差值的数组
667. Beautiful Arrangement II(Medium)
Given two integers n and k, you need to construct a list which contains n different positive integers ranging from 1 to n and obeys the following requirement:
Suppose this list is [a1, a2, a3, … , an], then the list [|a1 - a2|, |a2 - a3|, |a3 - a4|, … , |an-1 - an|] has exactly k distinct integers.
If there are multiple answers, print any of them.
Example 1:
Input: n = 3, k = 1
Output: [1, 2, 3]
Explanation: The [1, 2, 3] has three different positive integers ranging from 1 to 3, and the [1, 1] has exactly 1 distinct integer: 1.
Example 2:
Input: n = 3, k = 2
Output: [1, 3, 2]
Explanation: The [1, 3, 2] has three different positive integers ranging from 1 to 3, and the [2, 1] has exactly 2 distinct integers: 1 and 2.
数组中有 n 个数 [1,n],用这些数构造数组,使得相邻元素差有 k 个。
问题分析:
让前 k+1 个数的差值分别为 k,k-1,k-1,……1。
前k+1个数为:1,k+1,2,k,3,k-1,4,k-2,5,……
经理论推导可以得到
如果k为奇数:前k+1个数为:1,k+1,2,k,3,k-1,4,k-2,5,……,(k+1)/2,(k+1)/2+1
如果k为偶数:前k+1个数为:1,k+1,2,k,3,k-1,4,k-2,5,……,k/2+2,k/2+1
剩下的数从 k+2 依次赋值,因为从 k+2 开始的数还没有使用,而且二者之差也被前面的差值包含了。
class Solution {
public:
vector<int> constructArray(int n, int k) {
vector<int>res(n,0);
res[0]=1;
for(int i=1,diff=k;i<=k;i++,diff--)
res[i]=(i%2==1)?res[i-1]+diff:res[i-1]-diff;
for(int i=k+1;i<n;i++)
res[i]=i+1;
return res;
}
};
11、数组的度
697. Degree of an Array(Easy)
Given a non-empty array of non-negative integers nums, the degree of this array is defined as the maximum frequency of any one of its elements.
Your task is to find the smallest possible length of a (contiguous) subarray of nums, that has the same degree as nums.
Example 1:
Input: [1, 2, 2, 3, 1]
Output: 2
Explanation:
The input array has a degree of 2 because both elements 1 and 2 appear twice.
Of the subarrays that have the same degree:
[1, 2, 2, 3, 1], [1, 2, 2, 3], [2, 2, 3, 1], [1, 2, 2], [2, 2, 3], [2, 2]
The shortest length is 2. So return 2.
Example 2:
Input: [1,2,2,3,1,4,2]
Output: 6
class Solution {
public:
int findShortestSubArray(vector<int>& nums) {
int n = nums.size();
map<int, vector<int>>m; //map第二个元素放元素对应的下标
for (int i = 0; i < n ; i++)
m[nums[i]].push_back(i);
int degree = 0;
for (auto iter : m)
degree = max(degree, (int)iter.second.size());
int minlen = n;
for (auto iter : m){
if(iter.second.size() == degree)
minlen = min(minlen, iter.second[iter.second.size()-1] -iter.second[0] +1);
}
return minlen;
}
};
12、对角元素相等的矩阵
766. Toeplitz Matrix(Easy)
A matrix is Toeplitz if every diagonal from top-left to bottom-right has the same element. Now given an M x N matrix, return True if and only if the matrix is Toeplitz.
Example 1:
Input:
matrix = [
[1,2,3,4],
[5,1,2,3],
[9,5,1,2]
]
Output: True
Explanation:
In the above grid, the diagonals are:
“[9]”, “[5, 5]”, “[1, 1, 1]”, “[2, 2, 2]”, “[3, 3]”, “[4]”.
In each diagonal all elements are the same, so the answer is True.
Example 2:
Input:
matrix = [
[1,2],
[2,2]
]
Output: False
Explanation:
The diagonal “[1, 2]” has different elements.
问题分析:
对于不是第一行或者第一列的每个元素,判断每个与左上角的元素是否相等,出现不相等,返回 false。
class Solution {
public:
bool isToeplitzMatrix(vector<vector<int>>& matrix) {
int row=matrix.size();
int col=matrix[0].size();
for(int i=0;i<row;i++){
for(int j=0;j<col;j++){
if(i>0 && j>0 && matrix[i][j]!=matrix[i-1][j-1])
return false;
}
}
return true;
}
};
13、数组嵌套
565. Array Nesting(Medium)
S[i] 是一个集合,集合的元素为 A[i], A[A[i]], A[A[A[i]]],……就这样一直嵌套下去,集合中的元素不能重复,求最长的集合 S 的长度
Example 1:
Input: A = [5,4,0,3,1,6,2]
Output: 4
Explanation:
A[0] = 5, A[1] = 4, A[2] = 0, A[3] = 3, A[4] = 1, A[5] = 6, A[6] = 2.
One of the longest S[K]:
S[0] = {A[0], A[5], A[6], A[2]} = {5, 6, 2, 0}
方法一:暴力搜索
对于每一个元素,搜索形成环,环中有多少元素。
class Solution {
public:
int arrayNesting(vector<int>& nums) {
int n = nums.size();
int res = 0;
for (int i = 0; i < n; i++){
int start = nums[nums[i]];
int count = 1;
while (nums[i] != start){
count++;
start = nums[start];
}
res = max(res, count);
}
return res;
}
};
时间复杂度:O(n2), 空间复杂度:O(1)
方法二:伴随数组
对于一个环来说,从任何一个节点访问,这个环中的元素都没必要再次访问了,可以用伴随数组表示每个元素是否访问。
class Solution {
public:
int arrayNesting(vector<int>& nums) {
int n = nums.size();
vector<int>visted(n, 0); //记录每个元素是否访问过,访问过为1
int res = 0;
for (int i = 0; i < n; i++){
if(visted[i] == 0){ //没有访问
int start = nums[nums[i]];
int count = 1;
visted[i] = 1;
while (nums[i] != start){
count++;
visted[start] = 1;
start = nums[start];
}
res = max(res, count);
}
}
return res;
}
};
时间复杂度:O(n)
空间复杂度:O(n)
方法三:取消伴随数组,直接修改原数组,将访问过的元素置为-1
class Solution {
public:
int arrayNesting(vector<int>& nums) {
int n = nums.size();
int res = 0;
for (int i = 0; i < n; i++){
if (nums[i] != -1){
int start = nums[i];
int count = 1;
nums[i] = -1;
while (nums[start] != -1){
count++;
int tmp = nums[start];
nums[start] = -1;
start = tmp;
}
res = max(res, count);
}
}
return res;
}
};
时间复杂度:O(n)
空间复杂度:O(1)
14、分隔数组
769. Max Chunks To Make Sorted(Medium)
有一个数组 arr,数组中的元素为 0,1,2,……arr.size() - 1,将数组分隔成几部分,使得每部分单独排序后再连起来,还是排序数组,求最多可以将数组分成多少块。
Example 1:
Input: arr = [4,3,2,1,0]
Output: 1
Explanation:
Splitting into two or more chunks will not return the required result.
For example, splitting into [4, 3], [2, 1, 0] will result in [3, 4, 0, 1, 2], which isn’t sorted.
Example 2:
Input: arr = [1,0,2,3,4]
Output: 4
Explanation:
We can split into two chunks, such as [1, 0], [2, 3, 4].
However, splitting into [1, 0], [2], [3], [4] is the highest number of chunks possible.
解题思路:
对于前 i 个元素,如果前 i 个元素的最大值等于 i-1,说明前 i 个元素可以分离出来单独排序,也就是说前 i 个元素为{0,1,……,i-1 },或者其他顺序排列的集合。
class Solution {
public:
int maxChunksToSorted(vector<int>& arr) {
int maxnum = 0, res = 0;
for(int i = 0; i < arr.size(); i++){
maxnum = max(maxnum, arr[i]);
if(maxnum == i) res++;
}
return res;
}
};
时间复杂度:O(n)
空间复杂度:O(1)