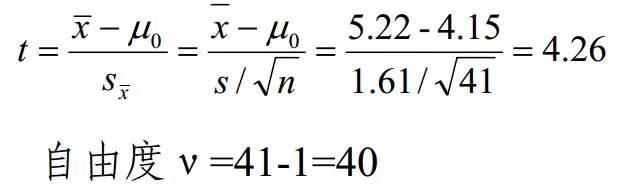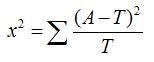统计学的那些冷门思考（各种检验+中心极限）

为了准备拼多多的数分岗，专门问了前讯飞同事关于统计数学中的一些冷门知识。

确实我当初和她讨论过，不过当时就忘了。今天专门写个博客以此纪念下来，人家可是老美数学出身，感觉学东西比我灵活，不那么死。今天把它分享出来，大家参考。

---------------------------- 开源 开放 无极限 -------------------------------

只讨论数学意义，拒绝公式。嘿嘿 很轻松明白

• 一、统计学中的检验

1. 正态检验

正态检验就是检验样本中是否满足正态分布，记得在前篇博客，讨论过偏态纠正（不妨正态化）的问题。本质是就是看看样本数据究竟有多像正态分布，给个pvalue和score，pvalue越低表示越好，score就是得分越高越好。

应用条件就很苛刻，哈哈哈。。。——得知道总体方差（我去，总体均值能get到，这知道总体方差也太难了我），但是知道总体方差太难了，除非是那些专家观察物理意义总结出来的，可以认为是这个整体的真正方差。（我们都是估计整体方差），所以使用其他就很难，所以就诞生了 t检验！

 

2. t检验（很常用）

t检验不需要知道总体方差，直接认为样本方差就是总体方差的估计。也就诞生了三个前提条件：

1.随机抽样 2.样本方差与整体方差近似 3.总体满足正态分布

可以看这三个条件，都指向了一个（用样本方差估计总体方差、且可以选用t检验代替正态检验）

t检验主要针对小样本，给个例子 https://www.jianshu.com/p/46d9b111dffc

样本与总体均数的比较：大量检测已知正常人血浆载脂蛋白E（apo E）总体平均水平为4.15mmol/L。某医师经抽样测得41例陈旧性心机梗死患者的血浆载脂蛋白E平均浓度为5.22mmol/L，标准差为1.61mmol/L。据此能否认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的平均浓度不一致？
（1）建立检验假设和确定检验水准。H0: μ=μ0，H1: μ≠μ0，α=0.05，双侧检验；

（2）选定检验方法和计算统计量。用单样本的t检验，

（3） 确定P值和作出推断结论。查t分布表， t0.05/2,40=2.021， t=4.26>t0.05/2,40，P<0.05。按α=0.05水准，拒绝H0，接受H1，可认为陈旧性心肌梗死患者的血浆载脂蛋白E平均浓度与正常人的差别有统计学意义，结合专业可以认为前者平均浓度较高。

从以上例子似乎可以知道，T检验的用途：（1）样本均数与群体均数的比较；（2）两样本均数的比较。说到底就是检验均值是否不同。

个人我觉得可以测试小样本能否代表整体样本（进而讨论你这种抽样合不合理）？

如果样本变大了，比如超过30了怎么办，就看z检验吧！

 

3. z检验

z检验主要针对大样本，主要有个中心极限定理（我后面讲），当认为样本近似的服从正态分布，当样本数量足够多时，样本方差和均值近似于总体均值和方差；或者，已知总体均值和方差，经过标准变换，认为其服从标准正态分布（z分布）（其实即使经过标准变换的值服从标准正态分布）。这就是z检验。

如果检验一个样本平均数x与一个已知的总体平均数μ的差异是否显著。其Z值计算公式为：

其中：x是检验样本的平均数；μ是已知总体的平均数；S是总体的标准差；n是样本容量。

【

1.当整体标准差已知的时候，就不需要用样本标准差去估计总体标准差了，所以都用z检验。

2.当总体标准差未知，需要估计，用t检验

】

当n>30，z检验和t检验结果相近，以t检验为准。z检验比较好计算，就在大样本时替代t。

可以看出z检验的适用性是不是很强！！！知道总体方差（标准差），Z test；不知道你随机多采点样本，用大量样本中的方差估计代替整体方差，继续z test。

假设检验H0 H1，你知道为啥 显著性水平α要选0.05吗，就是考虑进去了抽样存在的偶然性，所以我们一般要给他5%的容忍度，95%以上的置信度。最终 分析样本是否能够代替整体！

可以看出，Z test也是为了看出一个样本平均数是否和总体平均数的差异性（和t test的目的相同 分析样本是否能够代替整体！）

 

4. F检验

http://www.algorithmdog.com/%e5%81%87%e8%ae%be%e6%a3%80%e9%aa%8c%e5%8e%9f%e7%90%86%e4%b8%89f%e6%a3%80%e9%aa%8c

观察到两组不同正态分布生成的数据，怎么判断是这两组正态分布的方差是否一致呢？这就要用到F检验了。F检验又叫方差齐性检验，用于检验两组服从正态分布的样本是否具有相同的总体方差，即方差齐性。

用来检验方差是否不同！

 

5. 卡方检验

卡方检验用于检验观测到的数据是否服从特定多项分布。

卡方检验的计算公式为：

其中，A为实际值，T为理论值。

x^2 用于衡量实际值与理论值的差异程度（也就是卡方检验的核心思想），包含了以下两个信息：
1. 实际值与理论值偏差的绝对大小（由于平方的存在，差异是被放大的）
2. 差异程度与理论值的相对大小

例1 卡方检验

以下为一个典型的四格卡方检验，我们想知道喝牛奶对感冒发病率有没有影响：

通过简单的统计我们得出喝牛奶组和不喝牛奶组的感冒率为30.94%和25.00%，两者的差别可能是抽样误差导致，也有可能是牛奶对感冒率真的有影响。

为了确定真实原因，我们先假设喝牛奶对感冒发病率是没有影响的，即喝牛奶喝感冒时独立无关的，所以我们可以得出感冒的发病率实际是（43+28）/（43+28+96+84）= 28.29%

所以，理论的四格表应该如下表所示：

即下表：

 

如果喝牛奶喝感冒真的是独立无关的，那么四格表里的理论值和实际值差别应该会很小。

根据卡方检验公式我们可以得出卡方值为：

卡方 = (43 - 39.3231)平方 / 39.3231 + (28 - 31.6848)平方 / 31.6848 + (96 - 99.6769)平方 / 99.6769 + (84 - 80.3152)平方 / 80.3152 = 1.077

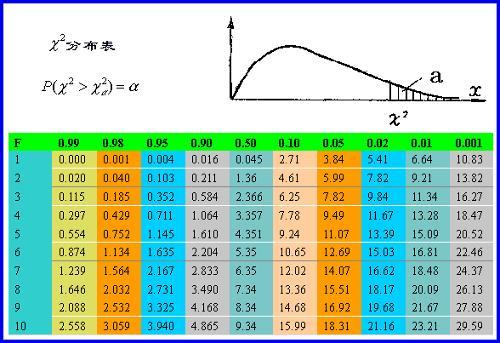
但是如何通过卡方的值来判断喝牛奶和感冒是否真的是独立无关的？也就是说，怎么知道无关性假设是否可靠？答案是，通过查询卡方分布的临界值表。（卡方值用来）

这里需要用到一个自由度的概念，自由度等于V = (行数 - 1) * (列数 - 1)，对四格表，自由度V = 1。

对V = 1，喝牛奶和感冒95%概率相关的卡方分布的临界概率是：3.84。即如果卡方大于3.84，则认为喝牛奶和感冒有95%的概率相关。

显然1.077<3.84，没有达到卡方分布的临界值，所以喝牛奶和感冒独立相关的假设不成立。

上面出现了卡方分布，其实卡方分布类似于伽马分布，他满足渐进正态性（中心极限定理中我再讲）。

卡方检验应用于特征选择（卡方检验用于分类问题）

卡方检验可以应用于特征选择（参考python特征选择那篇博客）。基于卡方检验的特征选择，计算每一个特征的卡方统计量，然后选择卡方统计量比较大的特征。假设文本分类中，类别一共只有两种“体育类”和“非体育类”。比如其中一个特征是文章是否包含词“篮球”。那么如下所示，会有四个项目——包括“篮球”体育类、包括“篮球”非体育类、不包括“篮球”体育类、不包括“篮球”非体育类。

按照这种方法，我们还可以计算s(排球，体育)，s(战斗机，体育),s(电视剧，体育)等不同特征的卡方统计量。一个特征的卡方统计量比较大，我们倾向于拒绝零假设（换句话说，我们倾向于认为该特征变量和类别变量不是相互独立的），从而保留这个特征。

不难发现，这个统计量的含义简而言之就是自变量对因变量的相关性。Python有包可以直接实现特征选择，也就是看自变量对因变量的相关性。今天我们先开看一下如何用卡方检验实现特征选择，用feature_selection库的SelectKBest类结合卡方检验来选择特征的代码如下：

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2

#选择K个最好的特征，返回选择特征后的数据
SelectKBest(chi2, k=2).fit_transform(iris.data, iris.target)

完整代码思路：

1. 首先import包和实验数据：

from sklearn.feature_selection import SelectKBest
from sklearn.feature_selection import chi2
from sklearn.datasets import load_iris
 
#导入IRIS数据集
iris = load_iris()
iris.data#查看数据
结果输出：
array([[ 5.1,  3.5,  1.4,  0.2],
       [ 4.9,  3. ,  1.4,  0.2],
       [ 4.7,  3.2,  1.3,  0.2],
       [ 4.6,  3.1,  1.5,  0.2],
       [ 5. ,  3.6,  1.4,  0.2],
       [ 5.4,  3.9,  1.7,  0.4],
       [ 4.6,  3.4,  1.4,  0.3],

2. 使用卡方检验来选择特征

model1 = SelectKBest(chi2, k=2)#选择k个最佳特征
model1.fit_transform(iris.data, iris.target)#iris.data是特征数据，iris.target是标签数据，该函数可以选择出k个特征 
结果输出为：
array([[ 1.4,  0.2],
       [ 1.4,  0.2],
       [ 1.3,  0.2],
       [ 1.5,  0.2],
       [ 1.4,  0.2],
       [ 1.7,  0.4],
       [ 1.4,  0.3],

可以看出后使用卡方检验，选择出了后两个特征。如果我们还想查看卡方检验的p值和得分，可以使用第3步。
3. 查看p-values和scores

model1.scores_  #得分

得分输出为：
array([ 10.81782088, 3.59449902, 116.16984746, 67.24482759])

可以看出后两个特征得分最高，与我们第二步的结果一致；

model1.pvalues_  #p-values

p值输出为：
array([ 4.47651499e-03, 1.65754167e-01, 5.94344354e-26, 2.50017968e-15])

可以看出后两个特征的p值最小，置信度也最高，与前面的结果一致。

关于p-value的碎碎念（小于α才好，而且越小越好）

这个pvalue就是用于检验特征与变量之间相关性的，假设你给出α值（常常取0.05，0.01），如果你的pvalue小于α，那就有把握认为，这个特征和预测变量y之间，具有相关性。比方说你取α=0.05，这就意味着你有95%（也就是1-α）的把握认为，这个特征和预测变量y之间存在相关性。

（这里立个flag，怎么分析单变量的特征筛选。目前得知有pearson、chi2、基于学习模型的单变量特征选择方法、还有互信息。改日我会出份博客专门讲单变量特征选择，而不是特征选择）

 

• 二、大数据量的分布规律

1. 大数定理

大数定律讲了一件什么事情？简单的来讲，它告诉我们在随机事件的大量重复出现中，往往呈现几乎必然的规律。在试验不变的条件下，重复试验多次，随机事件的概率近似于它出现的频率。

举个例子，投硬币。一枚硬币被抛出后有50%的可能为正面或者背面，在小样本的情况下，随机抛硬币的结果可能并不明显或者说结果没有规律，不稳定等等等等，10次里可能有4次正面6次背面，也可能是7次正面3次背面，这很正常。但是随着我们抛硬币的次数的增多，正面和反面出现次数就会越来越接近于相同。

大数定律以严格的数学形式表现了随机现象最根本的性质之一：平均结果的稳定性。

贝努利大数定律：事件发生的频率依概率收敛于事件的概率，明确了频率的稳定性。当N很大时，事件发生的频率与概率有较大偏差的可能性很小。

这个版本定义从概率的角度，当N很大的时候，事件A发生的概率等于A发生的频率。

2. 中心极限定理

自然界与生产中，一些现象受到许多相互独立的随机因素的影响，如果每个因素所产生的影响都很微小时，总的影响可以看作是服从正态分布的.。

首先从渐进正态性说起：当某一分布满足加和规律时，他绝对满足渐进正态性的（当样本足够大时，他就会变得越来越像正态分布，比如泊松、t、卡方分布）。这里指的是所有数据的分布满足近似正态性。

那么中心极限定理指的是数据量较大时，他数据样本的均值分布满足近似正态性。

中心极限定理是许多统计活动的“动力源泉”，这些活动存在着一个共同的特点，那就是使用样本对总体进行估计，例如我们经常看到的民意调查就是这方面的经典案例。

那么，什么是中心极限定理呢？

中心极限定理是说：
样本的平均值约等于总体的平均值。
不管总体是什么分布，任意一个总体的样本平均值都会围绕在总体的整体平均值周围，并且呈正态分布。

也就是说，当总体分布是正态分布时，对任意样本量n，抽样均值分布均为正态分布；如果总体为非正态分布，仅在n值较大（n一般大于30，那z检验不就用样本表示总体吗，哦原来它是有中心极限定理支持的）的情况下，样本均值分布近似为正态分布。【在独立同分布的情况下，无论分布函数是啥，它们的平均数，当充分大的时候总是近似地服从正态分布】

中心极限定理的通俗解释？

1）根据中心极限定理，我们可以得出的第1个结论是：任何一个样本的平均值将会约等于其所在总体的平均值。

例如你久居大城市，过年回老家，大街上遇到了邻居大妈，虽然20年没见你，邻居大妈还是一眼认出你了，这不是隔壁老王家的孩子嘛，长的真带劲。

这里，你爸妈就是总体，你就是你爸妈的样本，和你爸妈长的相似。同样的，一个正确抽取的家庭样本应该能够反映中国所有家庭的情况，里面会包含收入高的公司高管，也会包括普通的员工，快递小哥、警察以及其他人，这些人出现的频率与他们在人口构成中的占比相关。

因此，我们能够推测，这个包含1000个中国家庭代表性样本的家庭财富的平均值约等于总体的平均值。

2） 样本平均值呈正态分布

在这个例子中，样本平均值将会围绕着群体平均值（也就是16.9万元）形成一条正态分布曲线。记住，群体本身的分布形态并不重要，中国家庭收入的分布曲线并非正态分布，但样本平均值的分布曲线却是正态分布。

如果我们连续抽取100次包含1000个家庭的样本，并将它们的平均值的出现频率在坐标轴上标出，那么我们基本可以确定在总体平均值周围将会呈现正态分布。

取样次数越多，结果就越接近正态分布；而且样本大小越大，分布就越接近正态分布。

 

中心极限定理有什么用呢？

1）在没有办法得到总体全部数据的情况下，我们可以用样本来估计总体

如果我们掌握了某个正确抽取样本的平均值和标准差，就能对估计出总体的平均值和标准差。

举个例子

1. 如果你是北京西城区的领导，想要对西城区里的各个学校进行教学质量考核。

同时，你并不相信各个学校的的统考成绩，因此就有必要对每所学校进行抽样测试，也就是随机抽取100名学生参加一场类似统考的测验。

作为主管教育的领导，你觉得仅参考100名学生的成绩就对整所学校的教学质量做出判断是可行的吗？

答案是可行的。中心极限定理告诉我们，一个正确抽取的样本不会与其所代表的群体产生较大差异。也就是说，样本结果（随机抽取的100名学生的考试成绩）能够很好地体现整个群体的情况（某所学校全体学生的测试表现）。

2. 同样的，一个正确抽取的家庭样本应该能够反映中国所有家庭的情况，里面会包含收入高的公司高管，也会包括普通的员工，快递小哥、警察以及其他人，这些人出现的频率与他们在人口构成中的占比相关。
因此，我们能够推测，这个包含1000个中国家庭代表性样本的家庭财富的平均值约等于总体的平均值。

3. 当然，这也是民意测验的运行机制所在。通过一套完善的样本抽取方案所选取的1200名美国人能够在很大程度上告诉我们整个国家的人民此刻正在想什么。

2）根据总体的平均值和标准差，判断某个样本是否属于总体

如果我们掌握了某个总体的具体信息，以及某个样本的数据，就能推理出该样本是否就是该群体的样本之一。这也是统计概率中假设检验的原理。

通过中心极限定理的正态分布，我们就能计算出某个样本属于总体的概率是多少。如果概率非常低，那么我们就能自信满满地说该样本不属于该群体。

推荐https://blog.csdn.net/xiuxin121/article/details/78756143，通过样本均值可以得出总体均值，那么样本方差能得出总体方差呢？（可能没取到某些异常数据，自然样本方差代替不了总体方差，哪有其他方法补救吗，使得样本方差近似于总体方差？肯定有的！）