快速傅里叶变换FFT与快速数论变换NTT入门
一.FFT引入.
离散傅里叶变换DFT,是一种用于将多项式从系数表示转化为点值表示的多项式变换.
快速傅里叶变换FFT,是一种 O ( n log n ) O(n\log n) O(nlogn)的傅里叶变换,在OI中占有重要地位,主要用与优化卷积过程.
卷积,即给定 a i , b i a_i,b_i ai,bi,求 c i = ∑ i = 0 n a i b n − i c_i=\sum_{i=0}^{n}a_ib_{n-i} ci=∑i=0naibn−i.
为什么要用FFT来优化卷积,因为一个卷积直接求的复杂度是 O ( n 2 ) O(n^2) O(n2)的…
二.系数表示与点值表示.
多项式主要有两种表示,一个是系数表示,另一个是点值表示.
系数表示:即、对于一个多项式 F ( x ) = ∑ i = 0 n a i x i F(x)=\sum_{i=0}^{n}a_ix^i F(x)=∑i=0naixi,用系数 a i a_i ai表示一个多项式被称为多项式的系数表示.
点值表示:对于一个多项式 F ( x ) = ∑ i = 0 n a i x i F(x)=\sum_{i=0}^{n}a_ix^i F(x)=∑i=0naixi,用 n + 1 n+1 n+1个点 ( x i , F ( x i ) ) (x_i,F(x^i)) (xi,F(xi))表示一个多项式被称为点值表示.
考虑在做卷积的时候,系数表示明显要用 O ( n 2 ) O(n^2) O(n2)的时间,而对于点值表示的两个多项式 A ( x ) , B ( x ) A(x),B(x) A(x),B(x),发现它们卷积起来的点值表示就是 ( x i , A ( x i ) B ( x i ) ) (x_i,A(x_i)B(x_i)) (xi,A(xi)B(xi)),也就是说时间复杂度为 O ( n ) O(n) O(n).
突然感觉卷积只需要 O ( n ) O(n) O(n)即可解决了.只是我们一般用的是系数表示,直接系数表示可是没法 O ( n ) O(n) O(n)卷积的,所以我们要在这两种形式之间转换.
三.点值与插值.
点值:多项式从系数表示点值表示.
插值:多项式从点值表示系数表示.
对于点值,我们可以随意带入 n + 1 n+1 n+1个横坐标 x 0 , x 1 , x 2 , . . . , x n x_0,x_1,x_2,...,x_n x0,x1,x2,...,xn,分别求得对应的 F ( x 0 ) , F ( x 1 ) , F ( x 2 ) , . . . , F ( x n ) F(x_0),F(x_1),F(x_2),...,F(x_n) F(x0),F(x1),F(x2),...,F(xn),时间复杂度 O ( n 2 ) O(n^2) O(n2).
这个东西的速度与直接系数表示做卷积同级了…
不管了考虑插值.我们得到 n + 1 n+1 n+1个点值 ( x 0 , F ( x 0 ) ) , ( x 1 , F ( x 1 ) ) , . . . , ( x 2 , F ( x n ) ) (x_0,F(x_0)),(x_1,F(x_1)),...,(x_2,F(x_n)) (x0,F(x0)),(x1,F(x1)),...,(x2,F(xn)),那么可以列出方程组:
{ x 0 0 a 0 + x 0 1 a 1 + ⋯ + x 0 n a n = F ( x 0 ) x 1 0 a 0 + x 1 1 a 1 + ⋯ + x 1 n a n = F ( x 1 ) ⋮ x n 0 a 0 + x n 1 a 1 + ⋯ + x n n a n = F ( x n ) \left\{\begin{matrix} x_0^0a_0+x_0^1a_1+\cdots+x_0^na_n=F(x_0)\\ x_1^0a_0+x_1^1a_1+\cdots+x_1^na_n=F(x_1)\\ \vdots\\ x_n^0a_0+x_n^1a_1+\cdots+x_n^na_n=F(x_n) \end{matrix}\right. ⎩⎪⎪⎪⎨⎪⎪⎪⎧x00a0+x01a1+⋯+x0nan=F(x0)x10a0+x11a1+⋯+x1nan=F(x1)⋮xn0a0+xn1a1+⋯+xnnan=F(xn)
我们就可以列出一个矩阵方程:
[ 1 x 0 x 0 2 ⋯ x 0 n 1 x 1 x 1 2 ⋯ x 1 n ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n x n 2 ⋯ x n n ] [ a 0 a 1 ⋮ a n ] = [ F ( x 0 ) F ( x 1 ) ⋮ F ( x n ) ] \left[\begin{matrix} 1&x_0&x_0^2&\cdots&x_0^n\\ 1&x_1&x_1^2&\cdots&x_1^n\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&x_n&x_n^2&\cdots&x_n^n \end{matrix}\right] \left[\begin{matrix} a_0\\ a_1\\ \vdots\\ a_n\\ \end{matrix}\right]= \left[\begin{matrix} F(x_0)\\ F(x_1)\\ \vdots\\ F(x_n)\\ \end{matrix}\right] ⎣⎢⎢⎢⎡11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0nx1n⋮xnn⎦⎥⎥⎥⎤⎣⎢⎢⎢⎡a0a1⋮an⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡F(x0)F(x1)⋮F(xn)⎦⎥⎥⎥⎤
这里有一个特殊矩阵的出现,即范德蒙矩阵.
范德蒙矩阵:我们将等式左边 ( n + 1 ) ∗ ( n + 1 ) (n+1)*(n+1) (n+1)∗(n+1)的矩阵称为范德蒙矩阵,表示为 V ( x 0 , x 1 , . . . , x n ) V(x_0,x_1,...,x_n) V(x0,x1,...,xn),即:
V ( x 0 , x 1 , . . . , x n ) = [ 1 x 0 x 0 2 ⋯ x 0 n 1 x 1 x 1 2 ⋯ x 1 n ⋮ ⋮ ⋮ ⋱ ⋮ 1 x n x n 2 ⋯ x n n ] V(x_0,x_1,...,x_n)= \left[\begin{matrix} 1&x_0&x_0^2&\cdots&x_0^n\\ 1&x_1&x_1^2&\cdots&x_1^n\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&x_n&x_n^2&\cdots&x_n^n \end{matrix}\right] V(x0,x1,...,xn)=⎣⎢⎢⎢⎡11⋮1x0x1⋮xnx02x12⋮xn2⋯⋯⋱⋯x0nx1n⋮xnn⎦⎥⎥⎥⎤
由于我们要求出的是 a i a_i ai,高斯消元就可以了,时间复杂度 O ( n 3 ) O(n^3) O(n3)…
直接比系数表示求卷积还慢了…
不过插值还是可以 O ( n 2 ) O(n^2) O(n2)求的,利用拉格朗日插值法即可.
然后就可以直接 O ( n 2 ) O(n^2) O(n2)求插值了,然而还是与系数表示直接卷积同级,常数还大的一匹…
不过从上面我们可以看到的是,一次多项式卷积的过程可以分这几步走:
1.首先注意到 C ( x ) = A ( x ) B ( x ) C(x)=A(x)B(x) C(x)=A(x)B(x),若 A , B A,B A,B的最高次指数为 n n n,那么 C C C的最高次指数为 2 n 2n 2n,所以我们先把 A , B A,B A,B的最高次指数填到 2 n 2n 2n.
2.多项式点值.
3.点值表示下多项式乘法.
4.多项式插值.
四.一些在下面会用到的复数知识.
虚数单位:虚数单位 i i i满足 i 2 = − 1 i^2=-1 i2=−1.
虚数:一个虚数可以用 a i ai ai来表示.
复数:一个复数可以表示为 z = a + b i z=a+bi z=a+bi,其中 a a a被称为实部, b b b被称为虚部, i i i为虚数单位.
复数集合符号为 C C C.
复数加减法:实部对应实部,虚部对应虚部.即:
z 1 = a 1 + b 1 i , z 2 = a 2 + b 2 i z 1 ± z 2 = ( a 1 + b 1 i ) ± ( a 2 + b 2 i ) = ( a 1 ± a 2 ) + ( b 1 ± b 2 ) i z_1=a_1+b_1i,z_2=a_2+b_2i\\ z_1\pm z_2=(a_1+b_1i)\pm(a_2+b_2i)=(a_1\pm a_2)+(b_1\pm b_2)i z1=a1+b1i,z2=a2+b2iz1±z2=(a1+b1i)±(a2+b2i)=(a1±a2)+(b1±b2)i
复数乘法:
z 1 = a + b 1 i , z 2 = a + b 2 i z 1 z 2 = ( a 1 + b 1 i ) ( a 2 + b 2 i ) = ( a 1 a 2 − b 1 b 2 ) + ( a 1 b 2 + a 2 b 1 ) i z_1=a+b_1i,z_2=a+b_2i\\ z_1z_2=(a_1+b_1i)(a_2+b_2i)=(a_1a_2-b_1b_2)+(a_1b_2+a_2b_1)i z1=a+b1i,z2=a+b2iz1z2=(a1+b1i)(a2+b2i)=(a1a2−b1b2)+(a1b2+a2b1)i
复数的几何意义:我们可以用一个直角坐标系的的 x x x轴来表示实部, y y y轴来表示虚部.即对于一个复数 z = a + b i z=a+bi z=a+bi,它在直角坐标系上表示为:
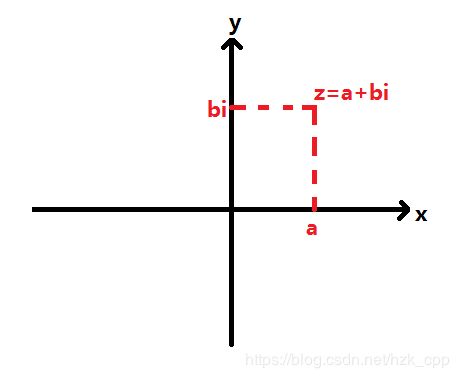
欧拉公式(复数在指数上的定义): e ϕ i = cos ϕ + i sin ϕ e^{\phi i}=\cos \phi+i\sin \phi eϕi=cosϕ+isinϕ.
欧拉恒等式: e π i + 1 = 0 e^{\pi i}+1=0 eπi+1=0,即 e π i = − 1 e^{\pi i}=-1 eπi=−1.
复数作为指数在极坐标系上的意义:对于 e u i = cos u + i sin u e^{ui}=\cos u+i\sin u eui=cosu+isinu,它在极坐标系上可以表示为:
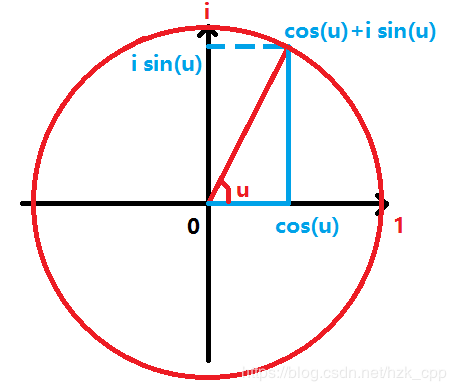
五.单位复数根.
单位复数根:一个 n n n次单位复数根定义为一个复数 ω \omega ω使得 ω n = 1 \omega^n=1 ωn=1,记为 ω n \omega_n ωn.
很明显对于任意一个正整数 n n n,有 n n n个 n n n次单位根恰好均匀分布在单位圆上.
例如 n = 8 n=8 n=8时:
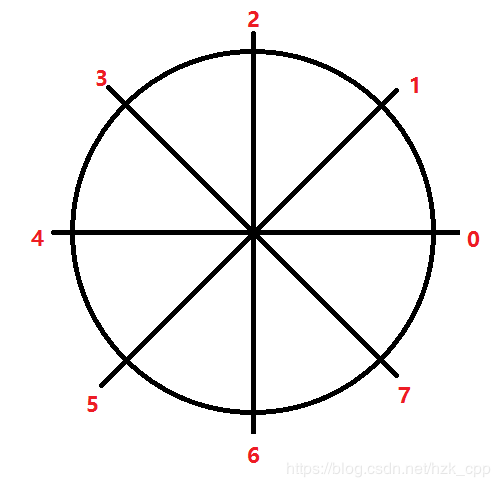
上图中 0 0 0到 7 7 7分别表示 ω 8 0 \omega_{8}^0 ω80到 ω 8 7 \omega_{8}^7 ω87.
根据欧拉定理和复数作为指数在极坐标系上的意义,可以得到:
ω n k = e 2 π i k n = ( e 2 π i n ) k \omega_{n}^{k}=e^{\frac{2\pi ik}{n}}=(e^{\frac{2\pi i}{n}})^{k} ωnk=en2πik=(en2πi)k
接下来我们给出三个引理:
引理1: ω d n d k = ω n k \omega_{dn}^{dk}=\omega_{n}^{k} ωdndk=ωnk.
证明: ω d n d k = e 2 π i d k d n = e 2 π i k n = ω n k \omega_{dn}^{dk}=e^{\frac{2\pi idk}{dn}}=e^{\frac{2\pi ik}{n}}=\omega_{n}^{k} ωdndk=edn2πidk=en2πik=ωnk.
引理2: ( ω n k + n 2 ) 2 = ( ω n k ) 2 (\omega_{n}^{k+\frac{n}{2}})^2=(\omega_{n}^{k})^2 (ωnk+2n)2=(ωnk)2.
证明: ( ω n k + n 2 ) 2 = ω n 2 k + n = ω n 2 k = ( ω n k ) 2 (\omega_{n}^{k+\frac{n}{2}})^2=\omega_{n}^{2k+n}=\omega_{n}^{2k}=(\omega_{n}^{k})^2 (ωnk+2n)2=ωn2k+n=ωn2k=(ωnk)2.
引理3:当 n ∣ k n|k n∣k时, ∑ j = 0 n − 1 ( ω n k ) j = 0 \sum_{j=0}^{n-1}(\omega_{n}^{k})^j=0 ∑j=0n−1(ωnk)j=0.
证明:
当 n ∣ k n|k n∣k时有:
∑ j = 0 n − 1 ( ω n k ) j = ( ω n k ) n − 1 ω n k − 1 = ( ω n n ) k − 1 ω n k − 1 = 1 k − 1 ω n k − 1 = 0 \sum_{j=0}^{n-1}(\omega_{n}^{k})^j=\frac{(\omega_n^k)^n-1}{\omega_n^k-1}=\frac{(\omega_n^n)^k-1}{\omega_n^k-1}=\frac{1^k-1}{\omega_n^k-1}=0 j=0∑n−1(ωnk)j=ωnk−1(ωnk)n−1=ωnk−1(ωnn)k−1=ωnk−11k−1=0
证毕.
六.傅里叶变换DFT.
傅里叶变换专门指从系数表示到点值表示的过程,也就是说这一部分介绍点值过程.
接下来我们假设 n n n一定是 2 2 2的整次幂,这可以让分治的过程好理解也好写很多.
考虑三个多项式 A ( x ) , A 0 ( x ) , A 1 ( x ) A(x),A_0(x),A_1(x) A(x),A0(x),A1(x),它们的关系如下:
A ( x ) = ∑ i = 0 n − 1 a i x i = a 0 + a 1 x + a 2 x 2 + . . . + a n − 1 x n − 1 A 0 ( x ) = ∑ i = 0 n 2 − 1 a 2 i x 2 i = a 0 + a 2 x 2 + a 4 x 4 + . . . + a n − 2 x n − 2 A 1 ( x ) = ∑ i = 0 n 2 − 1 a 2 i + 1 x 2 i + 1 = a 1 x + a 3 x 3 + a 5 x 5 + . . . + a n − 1 x n − 1 A(x)=\sum_{i=0}^{n-1}a_ix^i=a_0+a_1x+a_2x^2+...+a_{n-1}x^{n-1}\\ A_0(x)=\sum_{i=0}^{\frac{n}{2}-1}a_{2i}x^{2i}=a_0+a_2x^2+a_4x^4+...+a_{n-2}x^{n-2}\\ A_1(x)=\sum_{i=0}^{\frac{n}{2}-1}a_{2i+1}x^{2i+1}=a_1x+a_3x^3+a_5x^5+...+a_{n-1}x^{n-1} A(x)=i=0∑n−1aixi=a0+a1x+a2x2+...+an−1xn−1A0(x)=i=0∑2n−1a2ix2i=a0+a2x2+a4x4+...+an−2xn−2A1(x)=i=0∑2n−1a2i+1x2i+1=a1x+a3x3+a5x5+...+an−1xn−1
若我们用一个 n n n次单位根 ω n k \omega_n^k ωnk代入,则:
A ( ω n k ) = a 0 + a 1 ω n k + a 2 ω n 2 k + . . . + a n − 1 ω n ( n − 1 ) k = ( a 0 + a 2 ω n 2 k + a 4 ω n 4 k + . . . + a n − 2 ω n ( n − 2 ) k ) + ω n k ( a 1 + a 3 ω n 2 k + a 5 ω n 4 k + . . . + a n − 1 ω n ( n − 2 ) k ) = A 0 ( ω n 2 k ) + ω n k A 1 ( ω n 2 k ) A(\omega_n^k)=a_0+a_1\omega_n^k+a_2\omega_n^{2k}+...+a_{n-1}\omega_{n}^{(n-1)k}\\ =(a_0+a_2\omega_n^{2k}+a_4\omega_{n}^{4k}+...+a_{n-2}\omega_{n}^{(n-2)k})+\omega_n^k(a_1+a_3\omega_n^{2k}+a_5\omega_{n}^{4k}+...+a_{n-1}\omega_n^{(n-2)k})\\ =A_0(\omega_n^{2k})+\omega_{n}^kA_1(\omega_n^{2k}) A(ωnk)=a0+a1ωnk+a2ωn2k+...+an−1ωn(n−1)k=(a0+a2ωn2k+a4ωn4k+...+an−2ωn(n−2)k)+ωnk(a1+a3ωn2k+a5ωn4k+...+an−1ωn(n−2)k)=A0(ωn2k)+ωnkA1(ωn2k)
然后我们要分别往 A 0 , A 1 A_0,A_1 A0,A1里面代入 n 2 \frac{n}{2} 2n个 n n n次单位根,可是应该代入哪些单位根呢?
根据引理2,我们发现 ω n 2 k = ω n 2 k m o d n \omega_n^{2k}=\omega_n^{2k\,\,mod\,\,n} ωn2k=ωn2kmodn,也就是说实际上只有 n 2 \frac{n}{2} 2n个值而已.
根据引理1,发现 ω n 2 k m o d n = ω n 2 k m o d n 2 \omega_n^{2k\,\,mod\,\,n}=\omega_{\frac{n}{2}}^{k\,\,mod\,\,\frac{n}{2}} ωn2kmodn=ω2nkmod2n,所以其实就是代入 n 2 \frac{n}{2} 2n个 n 2 \frac{n}{2} 2n次单位根.
这样子分治很明显时间复杂度为 T ( n ) = 2 T ( n 2 ) + O ( n ) = O ( n log n ) T(n)=2T(\frac{n}{2})+O(n)=O(n\log n) T(n)=2T(2n)+O(n)=O(nlogn).
七.傅里叶逆变换IDFT.
接下来我们讨论如何插值,即从点值表示到系数表示.
考虑上面的范德蒙矩阵,我们现在拥有的矩阵方程为:
[ 1 ω n ω n 2 ⋯ ω n n − 1 1 ω n 2 ω n 4 ⋯ ω n 2 ( n − 1 ) ⋮ ⋮ ⋮ ⋱ ⋮ 1 ω n n − 1 ω n 2 ( n − 1 ) ⋯ ω n ( n − 1 ) 2 ] [ a 0 a 1 ⋮ a n − 1 ] = [ F ( ω 0 ) F ( ω 1 ) ⋮ F ( ω n − 1 ) ] \left[\begin{matrix} 1&\omega_n&\omega_n^2&\cdots&\omega_n^{n-1}\\ 1&\omega_n^2&\omega_n^4&\cdots&\omega_n^{2(n-1)}\\ \vdots&\vdots&\vdots&\ddots&\vdots\\ 1&\omega_n^{n-1}&\omega_n^{2(n-1)}&\cdots&\omega_n^{(n-1)^2} \end{matrix}\right] \left[\begin{matrix} a_0\\ a_1\\ \vdots\\ a_{n-1}\\ \end{matrix}\right]= \left[\begin{matrix} F(\omega_0)\\ F(\omega_1)\\ \vdots\\ F(\omega_{n-1})\\ \end{matrix}\right] ⎣⎢⎢⎢⎢⎡11⋮1ωnωn2⋮ωnn−1ωn2ωn4⋮ωn2(n−1)⋯⋯⋱⋯ωnn−1ωn2(n−1)⋮ωn(n−1)2⎦⎥⎥⎥⎥⎤⎣⎢⎢⎢⎡a0a1⋮an−1⎦⎥⎥⎥⎤=⎣⎢⎢⎢⎡F(ω0)F(ω1)⋮F(ωn−1)⎦⎥⎥⎥⎤
现在我们用 V V V表示范德蒙矩阵,用 a ⃗ \vec{a} a表示 a i a_i ai组成的矩阵,并且用 F F F表示等式右边的矩阵.
经过上面的讨论,我们要得到 V V V的逆矩阵 V − 1 V^{-1} V−1来得到 a ⃗ \vec{a} a,即 a ⃗ = V − 1 F \vec{a}=V^{-1}F a=V−1F.
由于 V − 1 V = E V^{-1}V=E V−1V=E, E E E为单位矩阵满足:
E i , j = { 1 i = j 0 i ≠ j E_{i,j}= \left\{\begin{matrix} 1&i=j\\ 0&i\neq j \end{matrix}\right. Ei,j={10i=ji=j
定理:对于一个范德蒙矩阵 V = ( 1 , ω n , ω n 2 , . . . , ω n n − 1 ) V=(1,\omega_n,\omega_n^2,...,\omega_n^{n-1}) V=(1,ωn,ωn2,...,ωnn−1), V j , k − 1 = ω n − k j n V^{-1}_{j,k}=\frac{\omega_n^{-kj}}{n} Vj,k−1=nωn−kj.
证明:
尝试证明 V V − 1 = E VV^{-1}=E VV−1=E,考虑第 ( j , j ′ ) (j,j') (j,j′)项:
( V − 1 V ) j , j ′ = ∑ k = 0 n − 1 V j , k − 1 V k , j ′ = ∑ k = 0 n − 1 ω n − k j n ω n k j ′ = ∑ k = 0 n − 1 ω n k ( j ′ − j ) n (V^{-1}V)_{j,j'}=\sum_{k=0}^{n-1}V^{-1}_{j,k}V_{k,j'}\\ =\sum_{k=0}^{n-1}\frac{\omega_n^{-kj}}{n}\omega_n^{kj'}\\ =\sum_{k=0}^{n-1}\frac{\omega_n^{k(j'-j)}}{n} (V−1V)j,j′=k=0∑n−1Vj,k−1Vk,j′=k=0∑n−1nωn−kjωnkj′=k=0∑n−1nωnk(j′−j)
根据引理3可得:
( V − 1 V ) j , j ′ = { 1 j = j ′ 0 j ≠ j ′ = E j , j ′ (V^{-1}V)_{j,j'}= \left\{\begin{matrix} 1&j=j'\\ 0&j\neq j' \end{matrix}\right. =E_{j,j'} (V−1V)j,j′={10j=j′j=j′=Ej,j′
证毕.
那么可以得到:
a j = 1 n ∑ k = 0 n − 1 F ( ω n k ) ω n − k j a_j=\frac{1}{n}\sum_{k=0}^{n-1}F(\omega_n^k)\omega_n^{-kj} aj=n1k=0∑n−1F(ωnk)ωn−kj
突然发现了什么,我们把 F ( ω n k ) F(\omega_n^k) F(ωnk)看成系数,把 ω n − k j \omega_n^{-kj} ωn−kj看成 ω n − k \omega_n^{-k} ωn−k的指数…
这不就是个卷积吗,FFT搞一下即可…
八.蝶形变换.
上面的FFT是递归而且要在函数内开数组,常数巨大而且容易爆栈,所以我们考虑能否写一个不用递归的FFT呢?
考虑递归的时候,把递归过程想象成一棵树,每一个节点所用的 a a a数组对应原来 a a a数组中的哪些下标:
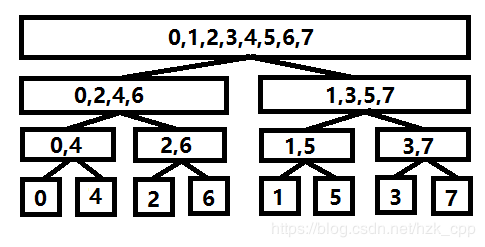
考虑自底向上一步步合并出原结果,那么我们要把这个东西按照叶子的位置重排一下.
这咋重排啊,这又没啥规律…搞成二进制看看吧:
0 000 000 0 4 100 001 1 2 010 010 2 6 110 011 3 1 001 100 4 5 101 101 5 3 011 110 6 7 111 111 7 0\,\,\,\,000\,\,\,\,000\,\,\,\,0\\ 4\,\,\,\,100\,\,\,\,001\,\,\,\,1\\ 2\,\,\,\,010\,\,\,\,010\,\,\,\,2\\ 6\,\,\,\,110\,\,\,\,011\,\,\,\,3\\ 1\,\,\,\,001\,\,\,\,100\,\,\,\,4\\ 5\,\,\,\,101\,\,\,\,101\,\,\,\,5\\ 3\,\,\,\,011\,\,\,\,110\,\,\,\,6\\ 7\,\,\,\,111\,\,\,\,111\,\,\,\,7 0000000041000011201001026110011310011004510110153011110671111117
突然发现叶子的顺序就是按照二进制翻转来的?那就二进制翻转好了.
怎么实现二进制翻转?考虑对于 i i i,把它向左移一位翻转后,再向左移一位,这是发现还有最高位可能为 1 1 1,判断原数最后一位是否为 1 1 1来判断是否要加.
九.快速数论变换NTT.
这一部分内容要涉及到原根,但不会涉及太多.想要详细了解原根可以去看高次同余方程之阶与原根,这里我们不详细展开了.
一个NTT模数一般来说要是 2 k x + 1 2^kx+1 2kx+1的形式,一般来说会是 998244353 , 1004535809 , 469762049 998244353,1004535809,469762049 998244353,1004535809,469762049,其中:
998244353 = 2 23 ∗ 119 + 1 1004535809 = 2 21 ∗ 479 + 1 469762049 = 2 26 ∗ 7 + 1 998244353=2^{23}*119+1\\ 1004535809=2^{21}*479+1\\ 469762049=2^{26}*7+1 998244353=223∗119+11004535809=221∗479+1469762049=226∗7+1
它们的原根都是 g = 3 g=3 g=3.
然后我们想起单位根要满足的性质为 ω n = 1 \omega^n=1 ωn=1,那么 ω n ≡ 1 ( m o d p ) \omega^n\equiv 1\,\,(mod\,\,p) ωn≡1(modp),其中 p p p是个质数,现在我们要求 ω \omega ω.
很显然 ω = g p − 1 n \omega=g^{\frac{p-1}{n}} ω=gnp−1,但是这时指数可不一定是个整数了,但是系数为 998244353 998244353 998244353或 1004535809 1004535809 1004535809时, n = 2 20 n=2^{20} n=220时没有问题的,而 n > 2 20 n>2^{20} n>220的时候一般就不会让你NTT了.所以遇到这两个指数直接搞即可.
想要知道更多NTT模数和原根的可以去看FFT用到的各种素数.
十.例题与代码.
题目:UOJ34.
FFT:
#includeNTT:
#include写在最后.
感谢rvalue神犇的blog教会了我FFT.
《算法导论》上的FFT也不错,虽然我没看完.